8. Implementáció¶
Mostanra az algoritmusunk kész van és megfelelően működik, azonban mi nem fejben vagy papíron szeretnénk végrehajtani a lépéseit, hanem egy számítógép segítségével. Az a baj, hogy a számítógép sem a folyamatábrát, sem a pszeudokódot nem érti meg közvetlenül. Az utasítássorozatunkat át kell alakítani olyan formára, amelyet a számítógép is tud értelmezni, azaz valós programozási nyelven kell megadnunk az algoritmust. Most következik tehát az implementáció, azaz a tényleges program megírása és tesztelése, a számítógépes megvalósítás.
8.1. Programozási nyelvek¶
Első lépésben meg kell ismerkednünk a valós programozási nyelvek néhány általános jellemzőjével és számos általános fogalommal.
8.1.1. Programozási nyelvek osztályzása¶
Az elmúlt évtizedekben nem csak egyféle számítógépes programozási nyelv fejlődött ki, hanem több száz. Ennek a jegyzetnek nem célja egyetlen konkrét nyelv részletes bemutatása, csak példaként szerepel benne néhány programsor demonstrációs céllal. Mint a jegyzet címe is mutatja a programozás alapjait próbáljuk meg általánosan áttekinteni.
A mai modern számítógépek és az őseik is a Neumann-elveknek megfelelően kettes számrendszer használnak, azaz mindent egyesek és nullák sorozatával írnak le. Ez alól nem kivételek a végrehajtható programok sem. Azonban binárisan programozni, nagyon nehézkes és manapság szinte senki sem ír közvetlenül gépi kódot.
Már viszonylag korán kialakult a programozásnak egy kicsit egyszerűbb módja az assembly. Ezen a számítógép architektúrához nagyon közeli szinten egyszerű utasításokkal adhatunk meg mindent, a számítógép számára elemi lépések formájában. Melyik adatot melyik regiszterbe tegyem? Hogyan állítsam elő a memóriacímet, ahová egy művelet eredményét el akarom menteni? A program megírásához szükség volt a számítógép konkrét felépítésének és működésének az ismeretére. Ha megírt valaki egy programkódot egy számítógépen azt valószínűleg nem tudta futtatni egy másikon, azaz ezen a második generációs programozási szinten a kódok nem voltak hordozhatóak. Kizárólag szemléltetésként álljon itt egyetlen Intel x86 architektúrára írt assembly utasítás.
sub eax, DWORD PTR [ebp-24]
Ez az egyetlen assembly utasítás azt jelenti, hogy van egy memóriacím az ebp regiszterben, ebből a címértékből vegyél el 24-et,
az így kapott memóriacímről olvass be egy dupla szó hosszúságú egész számot, ezt vond ki abból az értékből, ami az eax regiszterben
van, végül a különbséget tárold el az eax regiszterbe felülírva annak korábbi tartalmát. Ugye milyen egyszerű?
Az 1950-es évek végétől kezdtek elterjedni az úgynevezett harmadik generációs nyelvek (3GL) vagy más néven a magas szintű programozási
nyelv-ek. Ezekre jellemző az absztrakció és hordozhatóság. A programozónak a fejlesztés során nem kell ismernie az architektúrát, nem
kell azzal foglalkoznia, hogyan is kerül át a paraméter értéke az alprogramhoz (a rendszer majd megoldja). Egy program futtathatóvá
tehető egy teljesen más felépítésű számítógépen is. A programkód az ember számára sokkal könnyebben értelmezhető és általában rövidebb
is. Az alábbiakban egy Java nyelvű utasítás látható.
if (Salary<100000) { Salary = Salary*1.1; }
Ennek megértése nem hiszem, hogy gondot okozna a pszeudokódot már ismerő olvasónak. Ha a Salary változó értéke kisebb, mint százezer,
akkor megnöveljük az értékét 10%-kal. Jóval absztraktabb, mint az assembly. Nem kell a programozónak azzal foglalkoznia, hogy pontosan hol is van a változó a memóriában,
sem azzal, hogy hamis feltétel után hol is van a következő utasítás.
Habár a harmadik generációs nyelvek ma is nagyon népszerűek, régóta használhatunk negyedik generációs nyelveket (4GL) is. Az absztrakció
itt még magasabb szintet ér el, próbál a nyelv még emberbarátabb lenni. Sok esetben már szinte természetes emberi nyelvnek tűnik az, amit
a programban olvasunk. Habár nem általános programnyelv, hanem adatbáziskezeléshez tervezték az SQL is a ebbe a csoportba sorolható.
SELECT name FROM people WHERE age=20
Aki tud angolul sejti a fenti SQL utasítás jelentését programozói előismeretek nélkül is: Válogasd ki a neveket az emberek táblából, ahol a kor az 20! Nem csak
azt nem tudjuk, hogy milyen regiszterek vannak a processzorban, még azt sem kell tudnunk hány és milyen változót alkalmazzunk közben. Bár
sejtjük, hogy bizonyos lépéseket közben ismételni kell, de magának a ciklusnak a szervezését is rendszer biztosítja.
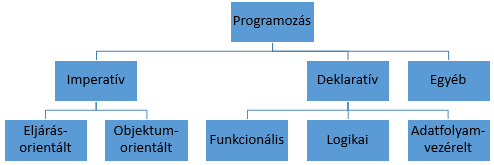
A programozási nyelvek gondolatmenete, szemlélete alapján különböző programozási paradigmákról beszélhetünk. A két legfontosabb paradigmába az imperatív és a deklaratív nyelvek csoportjai tartoznak. Az imperatív programozás utasításokra és változókra épül. A programozó feladata, hogy megadja az utasítások megfelelő sorrendjét, aminek hatására a megfelelő változók a megfelelő időpontban a megfelelő értékkel rendelkeznek, azaz a program egy bizonyos állapotban lesz. Tehát a fejlesztés során a programozónak el kell készítenie egy algoritmust, aminek a végrehajtása megadja az elvárt eredményt. Mint ahogy a latin imperium szó is kifejezi, utasítgatjuk a gépet. A legtöbb programozó ezzel találkozik először, a pszeudokód logikája is erre hasonlít.
Ezzel szemben a deklaratív nyelvek esetén azt kell megadnunk mi a probléma, mi a feladat, a megoldás menetét majd a rendszer szolgáltatja a matematikai logika vagy a függvénykalkulus alapján. A hogyan helyett a mit kell leírnunk a programban, amit kijelentő módban írunk. A változó a matematikai ismeretlen fogalmának felel meg, és így nincs is értékadás. Ciklusok helyett a rekurzív logika az alapértelmezett. Filozófiája teljesen eltér az imperatív nyelvek gondolatvilágától.
Az imperatív nyelvek világát két jelentősebb csoport alkotja: az eljárásorientált nyelvek és az objektumorientált nyelvek. Az eljárásorientált nyelveket a moduláris felépítés jellemzi. Szorosan kapcsolódnak a Neumann-architektúrához. A változók segítségével tárolt adatokon végzett műveleteket eljárások és függvények írják le. Ebbe a családba tartoznak például a C, a Pascal, a Fortran, a PL/I és a BASIC programozási nyelvek.
Az objektumorientált nyelvek az adatokat és a műveleteiket egységekét kezelik. Ez lesz az osztály, amelynek egy példány az objektum. Az osztályok nem függetlenek, hanem örökölhetnek jellemzőket más osztályoktól. Ez egy absztraktabb megközelítés, mint az eljárásorientált nyelveké. A leggyakrabban használt objektumorientált nyelvek a Java, a C++, a C#, a Python és a PHP.
A deklaratív világ egyik legfontosabb alcsoportja a logikai programozás, ami a matematikai logikán alapul. A program tényekre és szabályokra épül. Egyértelműen a legelterjedtebb képviselője a csoportnak a Prolog nyelv.
A deklaratív paradigmába tartozik a funkcionális programozás, ahol minden függvényként van értelmezve (még a konstansok is) és a megoldáshoz egy függvénykiértékeléssel jutunk. Nincs változó, így könnyen bizonyítható egy program helyessége. Alapjául a lambda-kalkulus szolgál. Ezt az elvet valló nyelvek többek között a Lisp, a Haskell, az F# vagy az Erlang.
A harmadik nagyobb deklaratív programcsalád az adatfolyam-vezérelt nyelvek csoportja. Itt a műveletek összeköttetésben állnak egymással (mint egy irányított gráf csomópontjai) és egy művelet azonnal végrehajtódik, ha minden bemenete elérhető lesz (ha az adatok megérkeznek, vagy ha bizonyos események bekövetkeznek). Távol állnak a Neumann-architektúrától, mivel alapvetően párhuzamos végrehajtást feltételeznek. Ide tartozik például a LabVIEW (G), a Verilog és a VHDL.
8.1.2. Implementációs hibák¶
Függetlenül attól milyen paradigmában is vagyunk, a program írás azt jelenti, hogy a programozó létrehozza a program forráskód-ját.
Ez a legtöbb programozási nyelv esetén (de nem mindig) egy szöveges fájl, aminek a tartalma az adott programozási nyelv formai és tartalmi
szabályrendszerének vagyis szintaxisá-nak megfelelő karaktersorozat. A szintaxis többek között meghatározza, hogy milyen karakterkészletet
használhatnunk, melyek a nyelv által lefoglalt kulcsszavak, hogyan válasszuk el az egyes utasításokat, hol kezdődhet egy utasítás, milyen jelölést használhatunk a
konstansokra, és így tovább. Ilyen szabályai a pszeudokódnak is voltak. Például nem lehetett else nevű változónk, a while után
szerepelnie kell egy do majd később egy enddo kulcsszónak is, a "darab" (idézőjelek között) egy egyszerű karaktersorozat például egy kimenetben,
míg a darab (idézőjelek nélkül) egy változó nevét jelölheti, stb. Ezek a szabályok minden nyelv esetén mások, más a nyelvek szintaxisa. Az alábbiakban egy
természetes szám faktoriálisának kiszámítására szolgáló függvény definícióját láthatjuk négy különböző nyelven.
Fortran nyelvű kód:
REAL FUNCTION FACT(N) FACT=1 DO 20 i=2,N 20 FACT=FACT*i RETURN END
Pascal nyelvű kód:
FUNCTION FACT(N:INTEGER):REAL; var i: integer; begin FACT:=1; i:=2; while i<=N do begin FACT:=FACT*i; i:=i+1; end; end;
C nyelvű kód:
int Fact(unsigned N){ int i, f=1; for(i=2;i<=N;i++) f*=i; return f; }
Python nyelvű kód:
def Fact(N): f=1 for i in range(2,N+1): f*=i return f
Első ránézésre a négy kód nagyon különböző (pedig mindegyik rokon nyelv, imperatív nyelvekről van szó). Ha alaposan megnézzük a logika mindegyik esetén ugyanaz, csak a külalak más. Ahhoz, hogy valaki meg tudjon írni egy programot, két dolog kell: képes legyen létrehozni a megfelelő algoritmust és ismerje egy valós nyelv szintaxisát. Az elsőként említett kompetencia elsajátítását segíti ez a jegyzet, a másodikhoz segítenek a „Programozási nyelvek 1-2” nevű tantárgyak.
Mint láttuk a szintaxis nagyon változatos lehet, de mind a négy programrészletben az alapvető lépések, az alkalmazott algoritmus azonosak. A programnak ezt a fajta jelentését, működésbeli viselkedését szemantiká-nak hívjuk. Az összes fenti esetben más lenne a kódok szemantikája, ha a szorzásjelek helyett összeadásjeleket használnánk, holott a szintaxis azt is megengedi. A szemantikát az algoritmus határozza meg.
Ezek alapján belátható, hogy például egy kisebb elgépelés különböző jellegű hibákhoz vezet, eltérő következményekkel járhat. Ha a formai
szabályokat sértjük meg ún. szintaktikai hibá-t vétünk. Ha például véletlenül endo szót írunk enddo helyett, akkor a
rendszer egyből érzékelni fogja, hogy nincs meg a do párja, nem lehet tudni, meddig tart a ciklusmag. Nem írhatunk if helyett
when szót, vagy az A és B változók szorzatát nem írhatjuk sem AB alakban, sem AxB alakban csak A*B formában.
A program biztosan nem fog lefutni ilyen hibák jelenléte esetén.
Más tévedések nem ennyire könnyen észrevehetőek. Ha az egyik programsorba az x=x+1 utasítás helyett az x=y+1 utasítást írjuk,
akkor ez még formailag elfogadható, nem sérti a szintaktikai szabályokat. A program akár le is futhat, csak az eredmény nem lesz az,
amit elvárunk. A tévedés az algoritmust változtatja meg. Ez a szemantikai hiba. A kifejlesztett tesztelési stratégia alkalmazásával
könnyen rájöhetünk, hogy baj van valahol, de a hiba pontos helyének felderítése sokkal nehezebb.
Néha a program szintaktikailag helyes, és alapvetően az elvárt eredményt adja, tehát a szemantikája is jónak tűnik, mégis bizonyos körülmények azt eredményezhetik, hogy a program elbukjon. Előfordulhat például, hogy a programunk egy konkrét fájl tartalmát szeretné beolvasni, korábban jól is működött a program, de a következő futtatás előtt letöröljük a fájlt. Ez a menet közben kiderülő futtatási körülmény a végrehajtás sikertelenségét eredményezi. Hasonló a helyzet, ha egy mennyiség négyzetgyökét szeretnénk kiszámolni, de az aktuálisan adott bemenetek éppen olyanok, hogy a mennyiség negatív lesz. Ezeket futási idejű hibá-nak nevezzük.
Azt szeretnénk egy utasításban megadni, hogy a C változó értéke legyen az A és B változók értékének hányadosa. Milyen
hibákat véthetünk közben? Ha C=A\B sort írunk, akkor az egy szintaktikai hiba, mivel a legtöbb nyelv esetén a visszafelé perjel
(\) nem egy kétoperandusú operátor (nem az osztás jele), így a sor nem értelmezhető. Megsértettük a szintaktikai szabályokat, a
program le sem fut. Abban az esetben ha C=A-B utasítást írunk, akkor ez formailag teljesen helyes, a program le is fut, de ha
figyelmesek vagyunk, észrevehetjük, hogy valószínűleg nem az elvárt eredményt kaptuk. Ez egy szemantikai hiba, mivel megváltoztattuk
az utasítás jelentését (hányados helyett különbség), nem a megfelelő algoritmust reprezentálja a program forráskódja. Amennyiben
C=A/B utasítást írunk, akkor mind formailag, mind a jelentését tekintve helyes programot kapunk, a program lefut és helyes eredményt
ad (általában). Viszont ha egyszer a B változó értéke nulla lesz, akkor a program „kiakad”, futási idejű hibával szembesülünk.
8.1.3. A forráskód elemei¶
Hogyan épül fel egy program? Mint már említésre került a forráskód legtöbb esetben egy szöveges állomány, karaktereket tartalmaz. Karakterekből épülnek fel a lexikális egységek, ezek alkotják a szintaktikai egységeket, amelyek az utasítások részei lehetnek. Az utasításokból programegységeket hozhatunk létre, ezekből áll a program. Ezek közül valamilyen formában már szinte mindegyik elemmel találkoztunk. Ebben az alfejezetben csak azokat emelnénk ki, amelyeket eddig nem említettük vagy a valós nyelvek esetén kiegészítésre szorulnak.
A karakterkészlet mindig tartalmaz betűket, számjegyeket és egyéb karaktereket. A nyelvek viszont eltérően kezelhetik ezeket a fogalmakat.
A legtöbb nyelv az angol ABC karakterein kívül betűnek tekinti például az aláhúzás jelet (_). Egyes nyelvek a kis és nagybetűket
megkülönböztetik, mások azt mondják, hogy a ProGraM és a pROgraM szavak azonosak. Néhány nyelvben használhatunk nemzeti nyelvi
betűket is.
A lexikai egységek közé tartoznak többek között a szimbolikus nevek (kulcsszavak, azonosítók), a konstansok és a megjegyzés. Az első két csoportról már korábban esett szó. A megjegyzés egy olyan karaktersorozat a forráskódban, ami a programozónak szól, a rendszer nem veszi figyelembe őket. Tehát nincs hatásuk a program végrehajtására, csak megkönnyítik a kód értelmezését az olvasó számára. Nagyon hasznos tud lenni, nem csak akkor, ha egy programon több programozó dolgozik, hanem magunk számára is érdemes lehet megjegyzéseket írni. Ha később vissza kell térnünk egy már megírt kódrészletre, a megjegyzések által könnyen megérthetjük mit, miért írtunk a kódba.
A szintaktikai egységek közé tartoznak a kifejezések. Megtanultuk, hogy ezek operátorokból és operandusokból és kerek zárójelekből állnak.
Tudjuk, hogy a műveleteknek van egy erősségi sorrendje (precedenciája), például a szorzás erősebb, mint az összeadás. A 2+3*4 kifejezés
és a 3*4+2 kifejezés ugyanazt az értéket jelenti, mert először a szorzást kell elvégeznünk. Az operátorok felírási sorrendje önmagában
nem dönti azt el, hogy melyikkel kezdődik a kiértékelés. Amennyiben a alapértelmezett kiértékelés sorrendjén változtatni szeretnénk, akkor
zárójeleket kell alkalmaznunk. Holott a (2+3)*4 kifejezésben az operátorok felírási sorrendje ugyanaz, mint a 2+3*4 esetén az
eredmény más lesz. A kifejezések ezen alakja nem egyértelmű.
Eddig kétoperandusú operátorok mindig az operandusaik között voltak. A 7 * 5 jelentése: a hetet szorozzuk meg öttel. Ezt infix kifejezés-nek
hívjuk. Korábban mindig csak ezt használtuk és a imperatív nyelvek is többnyire azt alkalmazzák. Azonban a kifejezéseket más
formában is fel lehet írni. Az egyik lehetőség az, hogy a kétoperandusú operátort követik sorban az operandusai. Például a * 7 5
kifejezés azt jelenti, hogy szorozzuk meg a hetet öttel. Ezt az alakot prefix kifejezésnek hívjuk. Egy harmadik lehetőség az, ha a
kétoperandusú operátor az operandusai után van. Tehát a 7 5 * kifejezés jelentése az, hogy a hét és az öt értékeket szorozzuk össze.
Ez az ún. posztfix kifejezés. Az előbbi kifejezések értéke mindhárom esetben 35, csak a külalak változik.
Mi a helyzet akkor, ha több operátor is van egy kifejezésben? Hogyan kell kiértékelni az ilyen összetett kifejezéseket? Vegyük először
a prefix esetet, a / * - 123 71 3 + 11 2 példa kifejezéssel! Itt az egyszerűség kedvéért minden érték konstans. A
kiértékelés menetét az alábbi természetes nyelven megadott algoritmus írja le.
Ha a kifejezés nem tartalmaz operátort, akkor kész vagy, egyébként menj tovább!
Balról jobbra haladva keresd meg az első olyan részkifejezést, ami
operátor konstans konstansalakú!Ezt az egyszerű prefix részkifejezést értékeld ki, vagyis hajtsd végre az adott műveletet az operandusokon!
A eredménnyel írd felül a most kiértékelt részkifejezést!
Folytasd az 1. lépéssel!
Ezek alapján a fenti kifejezés kiértékelésének a lépései a következők lesznek:
/ * - 123 71 3 + 11 2 / * 52 3 + 11 2 / 156 + 11 2 / 156 13 12
A posztfix kifejezések kiértékelésének módja nagyon hasonló, csak a keresett részkifejezés más.
Ha a kifejezés nem tartalmaz operátort, akkor kész vagy, egyébként menj tovább!
Balról jobbra haladva keresd meg az első olyan részkifejezést, ami
konstans konstans operátoralakú!Ezt az egyszerű posztfix részkifejezést értékeld ki, vagyis hajtsd végre az adott műveletet az operandusokon!
A eredménnyel írd felül a most kiértékelt részkifejezést!
Folytasd az 1. lépéssel!
A 123 71 - 3 * 11 2 + / kifejezés kiértékelésének lépései tehát a következők.
123 71 - 3 * 11 2 + / 52 3 * 11 2 + / 156 11 2 + / 156 13 / 12
Mint látható mind a prefix, mind a posztfix példánk értéke ugyanaz. Ez nem véletlen ugyanis mindkettő ugyanaz a kifejezés csak eltérő
alakban. Ez a kifejezés infix formában így néz ki: ( 123 - 71 ) * 3 / ( 11 + 2 ). Vegyük észre, hogy ezt az infix kifejezést
zárójelek nélkül nem tudjuk felírni, mert akkor mást jelentene. A másik két formában minden kifejezést fel tudunk írni zárójelek nélkül is.
Ki kell hangsúlyoznunk azt is, hogy prefix és posztfix alakban nincs az operátoroknak precedenciájuk, a kiértékeléshez nem kell tudnunk,
hogy melyik az erősebb operátor, a felírás mindig egyértelműen eldönti a kiértékelés sorrendjét. Ez különösen akkor lehet hasznos, ha
figyelembe vesszük, hogy például a C nyelvben 46 különböző operátor van és egy jó programozónak fejből tudnia kell ezek pontos
erősorrendjét, mivel ott csak infix kifejezést használhatunk. A deklaratív nyelvek előszeretettel alkalmaznak nem infix alakot. A prefix alak egy másik tipikus előfordulása megfigyelhető
például az MS Excel táblázatkezelőben is. Ott egy 4 ^ ( 2 + 1 ) * 3 kifejezés (ahol a ^ operátor a hatványozást jelenti) így
néz ki:
A szintaktikai egységekre (például a kifejezésekre) épülnek következő szintként az utasítások. Ezekre is láttunk már példát pszeudokódban,
gondoljunk csak az input/output utasításokra, az értékadásra, az eljáráshívásra, az elágaztatásra (if-then-else-endif szerkezet)
vagy a ciklusokra (while-do-enddo szerkezet). A valós programnyeleken ezek közül néhánynak több formája is lehet, illetve vannak további
utasítások. Ezeket a következő bekezdések foglalják össze röviden.
A pszeudokódban amikor csak eszünkbe jutott kitaláltunk és használtunk egy új változót gond nélkül. Számos valós nyelv megköveteli, hogy első használat előtt tisztázzunk pár dolgot az új változóval kapcsolatban. Ezt nevezzük deklaráció-nak. Azokban a nyelvekben, ahol a deklarációs utasítás szükséges, ott azt kell megadnunk ebben az utasításban, hogy az adott nevű változóban milyen jellegű adatokat és milyen módon szeretnénk tárolni. Később még foglakozni fogunk azzal, hogy például máshogy tárolódnak az egész számok és a valós számok, a szövegek pedig természetesen mindkettőtől eltérő módon. Ezen felül más műveleteket is végezhetünk rajtuk (valós számokat nem lehet maradékosan osztani, szövegeket nem lehet hatványozni, stb.). Ezek alapján az adatokat típus-okba sorolhatjuk. A típusos nyelvek esetén a deklarációs utasításban kell megadnunk egy új változó típusát és később ezen nem is változtathatunk.
Pszeudokódban egyetlen módszert alkalmaztunk az iteráció megvalósítására, azonban valós nyelvek esetén számos további ciklusszervező
utasítás is elérhető. A korábban alkalmazott while-do-enddo szerkezet a feltételes ciklus-ok közé tartozik, mivel egy logikai
feltétel dönti azt el, hogy kell-e ismételnünk a magot. A mag végrehajtása előtt a feltétel mindig kiértékelődik, tehát ez egy
kezdőfeltételes ciklus volt. Ilyet a legtöbb valós nyelv alkalmaz. Van viszont végfeltételes ciklus is sok nyelvben. Ennél a ciklusmag
egyszer mindenképpen végrehajtódik, majd kiértékelődik a ciklus végén megadott feltétel. Ha ez igaznak bizonyul a mag újra lefut,
különben mehetünk a következő utasításra. Így a ciklus sohasem lehet üres ciklus.
A ciklusok egy teljesen más logikát követő csoportja az ún. előírt lépésszámú ciklus. Itt mindig van egy ciklusváltozó, aminek van egy kezdőértéke, egy végértéke és egy (előjeles) lépésköze. Ez az értékehármas meghatároz egy intervallumot és abban értékek egy véges rendezett sorozatát. A ciklusváltozó minden egyes értéket felvesz ezek közül és a mag ezekkel fut le minden alkalommal. Már a ciklus megkezdése előtt meg lehet mondani, hogy hányszor fog lefutni a ciklus, nem úgy, mint a feltételes esetben. Nem minden nyelv használja. A valós programnyelvek némelyike az eddigiektől eltérő ciklusokat is ismer (pl. felsorolásos ciklus, formailag végtelen ciklus), de ezek nem ismertek széles körben.
Mint említettük az utasítások programegységeket alkothatnak. Az alprogramok, tehát a függvény és az eljárás is programegységek. Ezeken kívül gyakran találkozhatunk még a blokk fogalmával, ami egy másik programegységben előforduló utasítások név nélküli csoportja. A blokknak fontos szerepe van a hatáskörkezelésben. További programegységek még a csomag, a taszk vagy az osztály is.
A fenti kiegészítésekkel át is néztük a forráskód főbb elemeit. Elkészülhetett a program forráskódja.
8.1.4. Programírástól a futtatásig¶
Amikor a programozó megír egy programot, az még nem futtatható közvetlenül. Ez még csak a forráskód, ami legtöbbször egy vagy több szöveges fájl. A processzorok csak gépi kódot tudnak futtatni, így valamilyen módszerrel át kell alakítanunk a forráskódot gépi kóddá. Erre többféle lehetőség is van. Vannak fordítóprogramos, interpreteres és hibrid technikát alkalmazó programozási nyelvek.
A fordítóprogramos nyelvek esetén létezik egy speciális program (fordítóprogram, complier), ami a forráskódot feldolgozza és egy ún. tárgykódot állít elő. A fordítóprogram előfeldolgozást, szintaktikai ellenőrzést, szemantikai elemzést, lexikai elemzést, optimalizálást és kódgenerálást hajt végre. Ha a forráskódban akár csak egyetlen szintaktikai hiba is van, akkor a folyamat megszakad, nem keletkezik tárgykód, a hibákról visszajelzést kapunk. Szintaktikai hibáktól mentes kód esetén ugyan előáll a tárgykód, de ez még nem futtatható.
A legtöbb esetben több forráskódból kell összeraknunk egy programot. Lehet, hogy egyes részeket nem is mi írtunk meg. Emiatt több tárgykódra is szükségünk lehet. Ahhoz hogy ezek a független tárgykódok együtt tudjanak működni, szükség van egy speciális programra, a kapcsolatszerkesztő-re (más néven linkerre). Ez a tárgykódú fájlokból előállít egyetlen futtatható fájl-t. Ezeknek például Windows operációs rendszerben .exe kiterjesztésük lehet.
Amikor elindítjuk a futtatható programunkat, akkor egy újabb rendszerkomponens, a betöltő (vagy loader) a fájl alapján betölti a gépi kódot a memóriába, létrehoz egy folyamatot, azaz egy végrehatás alatt álló programot, és átadja a vezérlést az új folyamatnak. A program ennek hatására elindul végre és lefut (ha nem ütközünk futási idejű hibába).
A fenti elven működő fordítóprogramos nyelvek egyik előnye, hogy csak egyszer kell előállítani a gépi kódot (egyszer kell a programot lefordítani) és utána az akárhányszor gyorsan futtatható. Olyan ez, mint amikor egy elvégzi valaki egy szöveg angol-magyar fordítását. Lehet, hogy sokáig tart, de csak egyszer kell megtenni, utána bármikor azonnal el tudjuk olvasni a lefordított magyar szöveget. Ha a fordítás sikeres biztosak lehetünk benne, hogy a program mentes mindenféle szintaktikai hibától. Ezt az elvet követik a C, a C++, a Pascal, az Fortran, a PL/I vagy a LabVIEW.
A programozási nyelvek egy másik nagy csoportja egy másik módszert, az interpreteres technikát használják. Ilyenkor a kiindulási
forráskódot egy parancsértelmező (vagyis interpreter) kapja meg, ami sorról-sorra elkezdi értelmezni és azonnal végre is
hajtani a programot (soronként végez lexikai/szintaktikai ellenőrzést, kódgenerálást, stb.) Amikor az első sor végrehajtódott, csak
akkor kezdi el értelmezni a második sort. Így az is előfordulhat, hogy néha rejtve marad egy szintaktikai hiba (később gondot fog okozni,
de egyelőre nem vesszük észre). Ez például akkor fordulhat elő, ha a hiba mondjuk egy elágazás else ágában van, de tesztelés során
mi csak az igaz ágat hajtottuk vége. Egy másik hátránya a hogy nincs közvetlenül futtatható kód, minden egyes program végrehajtáskor
az interpreter látja el a processzort gépi kódokkal (az értelmezés után), emiatt az interpreteres futtatás mindig lassabb lesz (minden
futtatásnál újra szükséges a forráskód értelmezése). Ez ahhoz hasonlít, mint amikor egy csak magyarul értő személyt folyamatosan
angolul instruálunk, így annak először meg kell kérnie a folyton vele lévő tolmácsot, hogy fordítsa le az instrukciókat (még akkor is,
ha tizedik alkalommal hallja ugyanazt). Az adott nyelv interpretere nélkül nem tudjuk futtatni az adott gépen a programot. Ezt az elvet
vallják a Python, a Perl, a PHP, a C# vagy a MATLAB.
Néhány nyelv a fenti két módszer egyfajta keverékét használja. A forráskódot először le kell fordítani egy speciális köztes kódra, az a bájtkód. Később ezt a leegyszerűsített kódot fogja interpreterként lépésről lépésre végrehajtani egy úgynevezett virtuális gép. Ezt a technikát alkalmazza a manapság nagyon elterjedt Java nyelv.
Az implementáció folyamata során egy ún. integrált fejlesztői környezet-et (IDE) szokás használni. Ez egy szoftvercsomag, amely lehetővé teszi a gyors és hatékony szoftverfejlesztést. Ez mindenképpen tartalmaz egy szövegszerkesztőt, ahol megírhatjuk a forráskód szövegét. Ezek a szövegszerkesztők általában nyelv érzékenyek. Ez azt jelenti, hogy ismerik az adott programozási nyelv szintaktikáját, így már gépelés közben képesek jelezni az esetleges szintaktikai hibákat. Általában különböző színnel jelölik a kód különböző funkciót betöltő karaktersorozatait (kulcsszavakat, azonosítókat, konstansokat, stb.). Számos esetben gépelés közben javaslatot tesznek a már begépelt szöveg értelmes kóddá történő automatikus kiegészítésére. Fordítóprogramos nyelvek esetén tartalmazzák magát a fordítóprogramot, és kapcsolatszerkesztőt, interpreteres nyelv esetén pedig a parancsértelmezőt. Van bennük a nyomkövetéshez, hibakereséshez különböző eszközrendszer. Tartalmazhatnak verziókövetési és projektkezelései lehetőségeket is. Természetesen futtatási környezetet is biztosítanak. Némelyik IDE több, mint egy nyelvet támogat. A legnépszerűbb integrált fejlesztői környezetek a teljesség igénye nélkül, a NetBeans, a CodeBlocks, az Eclipse, a Dev-C++, a Microsoft Visual Studio, és a PyCharm.
A programozási nyelvekkel való általános ismerkedés után át kell tekintenünk hogyan is tárolja a számítógép az adatokat. Erről szól a következő alfejezet.
8.2. Adatábrázolás számítógépen¶
Ahhoz, hogy egy nyelven jól tudjunk programozni és a programunk megfelelőképpen működjön, tudnunk kell, hogy az adott rendszer hogyan is tárolja pontosan az adatainkat. Adatábrázolás és adattárolás részletei jelentősen befolyásolják mind a tervezés, mind az implementáció folyamatát.
A mai számítógépek a Neumann-elveknek megfelelően mindent binárisan, vagyis kettes számrendszerben tárolnak. Ezért egy informatikusnak
ismernie kell, hogyan működik ez a számrendszer. Emiatt kicsit részletesebben kell most foglalkoznunk a témával, mint korábban. A hétköznapi életben tízes (decimális) számrendszert használunk, ami azt jelenti, hogy minden számot
10 különböző számjegy segítségével adunk meg. Egy szám minden helyiértékéhez hozzárendeljük a számrendszer alapszámának egyik hatványát.
Ezek alapján például az 5738 jelentését megadhatjuk 5*1000 + 7*100 + 3*10 + 8*1 alakban. A számokat sorba tudjuk rendezni: 0,
1, 2, …, 9. Ezután, mivel nincs több eltérő számjegyünk egy trükköt alkalmazunk. Az adott helyiértéken a 9 helyett a 0 számjegyet
írjuk le és az előtte lévő helyiértéken eggyel nagyobb számjegyet alkalmazzunk megkapva a 10-et.
Ugyanezt a logikát alkalmazva, tehát a kettes számrendszerben összesen két féle szimbólumunk van (a 0 és az 1, ebben a sorrendben).
Egy kettes számrendszerben megadott, vagyis bináris szám értéke itt is a helyiértékeken és az alapszám (2) hatványain alapul. A
bináris 100110 értéke tehát 1*32 + 0*16 + 0*8 + 1*4 + 1*2 + 0*1 vagyis ez a decimális 38. A számolás itt is ugyanazon elvekre
épül, mint tízes számrendszerben csak összesen két számjegyünk van: 0, 1. Mivel elfogytak a számjegyek az 1 helyére 0-t
írunk és az előző helyiértéken vesszük a következő számjegyet (ha kell rekurzívan), azaz a sorrendben következő bináris érték az 10,
majd az 11. A legkisebb helyiértéken ezután az 1 helyére 0 és vennünk kell a sorban következő számjegyet a megelőző helyiértéken.
Viszont ott is 1 szerepel, azaz ezt is 0-ra cseréljük és vesszük az azt megelőző helyiértéken a következő számjegyet, vagyis a
következő bináris szám az 100. És így tovább. Az első 16 bináris pozitív egész szám tehát így néz ki:
Látható, hogy a legkisebb helyiértéken a két érték folyton váltakozik, előtte minden második lépésben, az azelőtti helyiértéken minden negyedik lépésben, majd 8, 16, 32, stb. lépésenként.
Néha egy tízes számrendszerbeli számot át kell váltanunk bináris alakra, néha pedig fordítva. Hogyan történik ez a konverzió? Egy általános valós szám decimálisból binárisba váltását leíró algoritmus így hangzik:
Az átváltott szám előjele ugyanaz legyen, mint a váltandó szám előjele.
Vedd először a váltandó számnak csak az egész részét!
Ha ez az érték
0, akkor folytasd a 7. lépéssel, különben menj tovább!Az értéket maradékosan oszd el kettővel és jegyezd meg a maradék értékét (
0vagy1)!Az értéket oszd el (hagyományosan is) kettővel és a hányados egész része legyen az új érték!
Folytasd a 3. lépéssel!
Írd ki a korábban megjegyzett maradék értékeket fordított sorrendben, vagy ha egy ilyen sem volt, akkor egy
0-t, majd írj le egy kettedes vesszőt!Vedd az eredeti átváltandó decimális számnak kizárólag a tört részét!
Ha ez
0(netán nem érdekel több tört helyiérték), akkor kész vagy, különben folytasd a következő lépéssel!Szorozd meg az értéket kettővel!
A szorzat egészrészét írd le a következő (kisebb) helyiértékre!
Az új vizsgált érték legyen az előbbi szorzat tört része!
Folytasd a 9. lépéssel!
Ezek alapján beláthatjuk, hogy a decimális -213.5625 érték a bináris -11010101.1001 alakban írható fel. Megjegyzendő,
a két szám értéke megegyezik, csak a felírásuk módja más. Számításunkat ellenőrizhetjük, ha elvégezzük a binárisból decimálisba
váltást, aminek az algoritmusa így is felírható:
Írd le az eredeti bináris szám előjelét!
Vedd a bináris szám legnagyobb helyiértékű számjegyét és jegyezd ezt meg!
Ha már nincs további egész helyiértékű számjegye a bináris számnak, akkor menj a 5. lépésre, különben a megjegyzett értéknek vedd a dupláját és add hozzá ezt következő bináris számjegyet! Most már ezt a számot tartsd fejben!
Folytasd a 3. lépéssel!
Írd le a megjegyzett számot majd egy tizedesvesszőt!
Jegyezd meg a
0számot és vedd a bináris szám legnagyobb tört helyiértékű számjegyét!Ha nincs további tört helyiértékű számjegye a bináris számnak, akkor menj a 9. lépésre, különben a megjegyzett értéknek vedd a dupláját és add hozzá a következő bináris számjegyet! Most már ezt a számot tartsd fejben!
Folytasd a 7. lépéssel!
Oszd el a megjegyzett számot kettőnek annyiadik hatványával, ahány tört tizedes jegy van az eredeti bináris számban!
Írd le a hányados tört részét a tizedesvessző után! Kész vagy.
Más számrendszerek is hasznosak lehetnek az informatikában. Ilyen például a gyakran alkalmazott tizenhatos (hexadecimális) számrendszer.
Itt 16 különböző számjegyünk van: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E és F. A számolás és átváltás logikája nagyon hasonló, mint
a kettes számrendszer esetén, csak a 2 helyett 16-tal kell az műveleteket (maradékos osztás, szorzás, stb.) elvégezni. Észrevehetjük,
hogy a bináris és a hexadecimális számrendszer között egy elég szoros kapcsolat van, ami megkönnyíti az egyikből a másikba történő
közvetlen átváltást. Ugyanis a 16 az nem más, mint a 2 negyedik hatványa. Emiatt egy négy bináris számjegyet tartalmazó csoport
felfogható egyetlen hexadecimális számjegyként. Például a bináris 11 0010 1110 1100 1101 1001 értéke megfelel a hexadecimális
32ECD9 értéknek (ami a decimális 3337433 értékkel egyenlő).
Amellett, hogy tudunk kettes számrendszerben számolni, hasznos lehet egy informatikus számára, ha matematikai műveleteket is tud végezni bináris számokkal. Most csak a bináris összeadás kerül bemutatásra, ezen belül is először a különálló számjegyek összege.
A
B
A+B
0
0
0
0
1
1
1
0
1
1
1
10
Az első három eset viszonylag egyértelmű. A negyediknél az eredmény bináris alakban már két számjegyű (ez a decimális 2). Több helyiértékű
számok összeadása esetén majd ilyenkor azt mondjuk, hogy az adott helyiértéken az eredmény 0, de keletkezett egy átviteli érték,
az 1, amit majd a következő helyiértéken való összeadásnál kell figyelembe vennünk. Ezek alapján láthatjuk, hogy általános esetben
három bináris helyiérték összeadását kell megvalósítanunk. Ezt foglalja össze a következő táblázat, ahol tehát A az összeadás első
tagjának adott helyiértékű számjegye, a B a másik tagé, C az előző helyiértéken keletkezett átvitel, D az eredmény adott
helyiértékű számjegye, míg E a következő helyiértékre átvinni szükséges érték.
A
B
C
D
E
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Ezek alapján az 101101010 és a 1101100 összege 111010110 (vagyis decimálisan 362+108=470).
Jó tudni, hogy minden matematikai műveletnek az algoritmusa használható bináris számokra is csak szem előtt kell tartanunk, hogy mindössze
két számjegyünk van. Ha például végrehajtunk egy szorzást bináris számok között, könnyen rájöhetünk, hogy kettes számrendszerben a
szorzótábla mindössze 4 elemű (a megszokott 100 helyett) és a négy érték közül ráadásul három 0.
Ahogy már említettük az informatikában mindent kettes számrendszerben írunk le. Egy bináris helyérték neve bit.
Természetesen egy bit két értéket vehet fel: 0 vagy 1.
A fentiek alapján bármit is szeretnénk a számítógépen tárolni, azt először számokká kell alakítanunk és ezeket a számokat bitek sorozataként felírnunk. Azt a folyamatot, amely során egy tetszőleges adatot bitsorozattá alakítunk kódolás-nak hívjuk. Ezt ne keverjük össze a titkosítással! A kódolás az adat egy eddigitől eltérő megjelenítési formája, amelynek értelmezése mindenki számára elérhető. Az ezzel ellentétes folyamat tehát, amikor egy bitsorozatot valamilyen adatként próbálunk meg értelmezni, dekódolás-nak hívjuk.
A kódolás menete sokféle lehet. Vegyünk egy példát! Minden nap az ebédhez gyümölcsöt szeretnénk fogyasztani. Összesen három gyümölcs
közül választhatunk: alma, banán, őszibarack. Ha az egyes választásokat el szeretnénk tárolni, azt számítógépen csak bitek formájában
tudjuk megtenni. Kódolnunk kell tehát a gyümölcsöket. Rendeljünk hozzájuk egy-egy (bináris) számot! Például legyen az „alma” az 1,
a „banán” a 2, és az „őszibarack” a 3. Mind a három értéket le tudjuk írni 2 bit segítségével, sőt mivel két biten 4 különbözőféle
kombináció is lehet az egyik bitpáros kihasználatlan lesz. Így tehát a gyümölcseink kétbites kódolása így néz ki:
gyümölcs
kód
alma
01
banán
10
őszibarack
11
kihasználatlan
00
Persze, ha akarunk a kihasználatlan bitpárnak is tulajdoníthatnunk értelmet, jelentse például a 00 kód azt, hogy aznap egyáltalán
nem fogyasztunk gyümölcsöt az ebédhez. Ha idővel bővülne a választék és választhatnánk körtét vagy szőlőt is a korábbiak mellett, akkor
a kétbites kódolás már nem lenne megfelelő. Hat (5 gyümölcs + a „semmi”) különböző dolog kódolásához már legalább 3 bit szükséges. Ennek
megfelelően az ENSZ által jelenleg elismert 193 ország kódolásához már 8 bit szükséges. Nyolc biten ugyanis 256 különböző bitkombináció
szerepelhet, míg hét biten csak 128 (ami nem elegendő).
Tehát minden adathoz egy számot kell rendelnünk és ezt a számot bitek sorozataként felírni. Ennek a második lépésnek, tehát a számábrázolás-nak számos szabványosított megoldása terjedt el az informatikában. Ezek sohasem tetszőleges számú bitet használnak, mert az technikailag rettentően megnehezítené a számítógép működését. Minden adat 8 bites egységekben kerül felhasználásra. A 8 bit együttes neve bájt. Egy adatot tárolhatunk, mondjuk 2 vagy 4 bájton, de sohasem 21 biten.
Nézzünk egy való életbeli számábrázolási szituációt! Az egyik legelterjedtebb (és legegyszerűbb) módja természetes számok tárolásának az ún.
előjel nélküli fixpontos számábrázolás. Ez sokszor 4 bájton történik, azaz a pozitív egész számokat és a nullát 32 biten tároljuk el,
egyszerűen úgy, hogy a szám kettes számrendszerbeli alakját vezető nullákkal kiegészítjük 32 bitre. Például a 2452132 értéket az
alábbi bitsorozat reprezentálja:
00000000 00100101 01101010 10100100
Könnyen belátható, hogy ez a technika korlátos, nem tudunk akármekkora számokat eltárolni. A tízmilliárd például bináris alakban 34 helyiértéket tartalmaz, így nem tárolható el 4 bájton.
Mi a helyzet a negatív számokkal? A fenti módszer definíció szerint nem foglalkozik negatív értékekkel, minimuma a nulla volt. Hogyan tároljunk
ennél kisebb egész számokat? A hétköznapokban egy extra szimbólumot (-) használunk a 10 számjegy szimbólum mellett. Azonban a számítógépen
csak 1-esek és 0-ák szerepelhetnek, nincs harmadik szimbólum. Egy trükkös megoldást kell alkalmaznunk, ami az előjeles
fixpontos számábrázolás névre hallgat. Ezt (negatív és pozitív) egész számok megjelenítésére is használhatjuk. A nulla és a pozitív
egészek ugyanúgy tárolódnak, mint az előjel nélküli esetben (bináris alakban szükség esetén vezető nullákkal kiegészítve). A negatív
értékek reprezentációjának kitalálásakor egy fontos elvet követtek elődeink: ugyanaz az összeadó algoritmus használható legyen mind pozitív,
mind negatív egész számok esetén is. Ennek a feltételnek a kielégítéséhez szükségünk van az egyes és kettes komplemens fogalmára.
Egy bitsorozat egyes komplemensén azt a bitsorozatot értjük, amelyben minden bit az eredeti bit ellentéte. Egy szám
kettes komplemense pedig nem más, mint a számot ábrázoló bitsorozat egyes komplemensénél egyel nagyobb bináris érték (adott számú biten). Ezek alapján írjuk
fel az előjeles fixpontos számábrázolás algoritmusát!
Jegyezd meg a reprezentálandó egész érték előjelét!
Írd le a szám abszolút értékét binárisan!
Egészítsd ki az eredményt vezető nullákkal!
Ha az eredeti szám negatív volt, akkor folytasd az 5. lépéssel, különben menj a 7. lépésre!
A teljes bitsorozatot váltsd át az ellentétére, azaz állítsd elő az egyes komplemensét!
A kapott bináris értékhez adjál hozzá egyet, azaz vedd a kettes komplemensét!
Ha az eredmény több hasznos bitet tartalmaz, mint megengedett (pl. 16, 32, 64 bit), akkor az érték nem ábrázolható ilyen feltételek mellett. Ellenkező esetben a bitsorozat végén lévő megfelelő számú bit (16, 32, 64) reprezentálja a kívánt előjeles egész számot.
Ismét látható, hogy ez a módszer is korlátos. Természetesen adott számú biten nem tárolhatunk akárhány értéket. Lesz egy minimum és
egy maximum, és ezek között minden egész szám ábrázolható lesz. Ennek a technikának van egy hasznos következménye. Ha az eredmény
bitsorozat első, legnagyobb helyiértékű bitje 1, akkor tudhatjuk, hogy az érték negatív ellenkező esetben pedig vagy nulla, vagy pozitív.
Emiatt ezt a bitet szoktuk előjelbitnek is nevezni.
A fentiek alapján tehát 2 bájtos előjeles fixpontos számábrázolás esetén a
+100 értéket a 00000000 01100100 bitsorozat reprezentálja, míg a -100 értéket az 11111111 10011100 bitsorozat formájában
kódolhatjuk a számítógépes szabvány szerint. Ha összeadjuk ezt a két értéket a korábban tanult bináris összeadás algoritmusát használva,
akkor az eredmény számunkra fontos utolsó 16 bitjén csak 0-k szerepelnek, ami a nulla egész szám kódja. Ez nem meglepő, hiszen a
+100 és a -100 összege 0, ami viszont fontos, az az, hogy így összeadással meg tudjuk valósítani a kivonást is. (Mivel
az A-B felírható (+A)+(-B) alakban.
Egy előre meghatározott tartomány összes egész számát már le tudjuk kódolni bitekre, de mi a helyzet a valós (tört) számokkal? Itt már nem csak a szám helyiértékeit kell tárolnunk, hanem a nagyságrendjét, azaz a tizedesvessző helyét is. Erre egy jól bevált és széleskörűen alkalmazott szabvány a lebegőpontos számábrázolás. Egy valós szám kódolása ilyen módszerrel elég összetett. A részletekkel a „Számítógép architektúrák” tantárgy keretében ismerkedhet meg az olvasó. Magyarázat nélkül a 4 bájtos (ún. egyszeres pontosságú) lebegőpontos számábrázolás menete általános esetben a következő:
Ha a reprezentálandó szám negatív, akkor a bitsorozat első értéke (előjelbit)
1legyen, különben0!Váltsd át a szám abszolút értékét kettes számrendszerbe!
A kettedes vesszőt told el a legelső
1-es bit mögé! (Vagyis szorozd meg az értéket 2 annyiadik hatványával, hogy az eredmény nagyobb vagy egyenlő legyen eggyel, de kisebb, mint a bináris kettő!) Ahány pozícióval balra került a kettedes vessző azt a számot nevezzük karakterisztikának! (Jobbra tolódás esetén ez negatív érték.) A kettedes vessző eltolása révén kapott bináris értéket nevezzük mantisszának!A karakterisztika értékéhez adj hozzá 127-et és az így kapott érték 1 bájtos bináris alakja legyen az eredmény következő 8 bitje!
A mantiszában a kettedes vessző után szereplő bitek legyenek az eredmény további bitjei! Ha ez több, mint 23 bitet jelent, akkor csak a kerekítés utáni első 23 bitre van szükség. Ha kevesebb, mint 23 (tört) bit szerepel a mantisszában, akkor
0bitekkel kell kiegészíteni 23 bitre!
Például ha a -193,1875 binárisan -11000001,0011 alakú, az előjel miatt a végeredmény első bitje 1. Az abszolút értékben
szereplő tizedesvessző eltolása után a mantissza 1,10000010011 lesz, a karakterisztika pedig 7 (mert ennyi pozícióval került
balra a tizedesvessző). A karakterisztika plusz 127, most 134-et jelent, ami 8 biten binárisan 10000110. A mantissza tört része
23 biten pedig 10000010011000000000000. Vagyis a -193,1875 értéket egyszeres pontosságú lebegőpontos számábrázolással kódoló
4 bájt így néz ki:
11000011 01000001 00110000 00000000
Látható tehát, hogy különböző céllal sokféle számábrázolási, kódolási technika van használatban. Emiatt egy adott bitsorozat mindig
többféle értéket is képviselhet. Az előbbi 32 bit tehát jelentheti a -193,1875 valós számot, de akár a -1019138048 egész számot,
a -15551 és +12288 együttes értékpárt, de akár a "ĂA0" karaktersorozatot is. A programozónak kell tudnia, hogy milyen
memóriaterületen, milyen reprezentációs technikával, milyen értéket tárol.
Ezt explicit módon segíti a számos programozási nyelv esetén használandó típus alkalmazása. Ezen nyelvek esetén a deklarációs utasításban minden változó esetén meg kell adni használat előtt annak típusát. Az egyes adattípusok eltérnek abban, hogy az ilyen típusú változók milyen értékeket vehetnek fel, azokat milyen bitsorozat reprezentálja a számítógépen, hogy rajtuk milyen műveleteket hajthatunk vége.
8.3. Szójegyzék¶
- assembly
A programozásnak egy olyan formája, amely filozófiáját tekintve nagyon közel áll a gépi kódhoz és hardveres ismereteket igényel a konkrét célrendszerre vonatkozóan.
- bájt
A számítógépes adattárolás alapegysége. 8 bitből álló adat neve, mely 256 különböző értéket képviselhet.
- bit
Kettes számrendszerbeli számjegy. Két lehetséges állapot képes reprezentálni
1és0értékekkel.- deklaráció
Az utasítások egy csoportja, amellyel egy változó nevét és típusát összerendelhetjük, és közben létrehozhatjuk magát a változót is a memóriában.
- dekódolás
A kódolással ellentétes folyamat, mely során egy bitsorozatot egy megfelelő adatként tudunk értelmezni.
- egyes komplemens
Egy bitsorozat össze bitjének az ellentétes bitre történő átváltása. Például a
01101100egyes komplemense az10010011.- előírt lépésszámú ciklus
Az iteráció egyik fajtája, ahol a ciklusváltozó egy megadott egyenközű értékkészlet elemeit feszi fel és mindegyik érték esetén egyszer lefut a ciklus magja.
- feltételes ciklus
A ciklusok azon csoportja, ahol egy feltétel határozza meg, hogy kell-e még futtatni a ciklus magját. A valós nyelvekben általában igaz feltétel esetén fut le a ciklusmag. Beszélhetünk kezdőfeltételes és végfeltételes altípusokról.
- fordítóprogram
Egy olyan szoftver, amely egy bizonyos programozási nyelven megírt forráskódot értelmezve előállít egy tárgykódot. Ilyen használ a C nyelv is.
- forráskód
A programozó által az adott nyelv szintaxisának betartásával létrehozott szöveges fájl. Közvetlenül nem futtatható, fordítóprogramos vagy interpreteres technika révén állítható elő belőle a processzor által érthető gépi kód.
- futási idejű hiba
Olyan programozási hiba, amelyet valamilyen a program futtatásának idején fellépő körülmény idéz elő. Például nullával való osztás, nem létező erőforráshoz való hozzáférési kísérlet, stb.
- futtatható program
A fordítás és linkelés során előállt állomány, melyet elindítva a benne található gépi kód a számítógép számára végrehajthatóvá válik. Tetszőleges számban futtatható (a fordítóprogram nélkül is).
- gépi kód
Bináris kód, amelyet a processzor közvetlenül is végre tud hajtani.
0és1bitek sorozataként tárolja az algoritmusban meghatározott elemi tevékenységeket.- implementáció
Az a folyamat, amely során a korábban megírt algoritmust egy valós programozási nyelven adunk meg számítógépen létrehozva a forráskódot. Az implementáció folyamatának része az elkészült program tesztelése is.
- infix kifejezés
A kifejezések olyan írásmódja, ahol a kétoperandusú operátorok az operandusok között vannak. Néha kötelező zárójeleket is használni. A kiértékelés sorrendjének meghatározásához ismernünk kell az egyes operátorok erősségét, azaz precedenciáját.
- integrált fejlesztői környezetet
Egy szoftvercsomag, amely a programozó számára lehetővé teszi a gyors és hatékony szoftverfejlesztést. Különböző szolgáltatásokkal segíti a fejlesztés folyamatát.
- interpreter
Egyes nyelvek által használt parancsértelmező, amely a program forráskódját utasításonként értelmezi és rögtön végre is hajtja azt. Nem állít elő tárgykódot és futtatható állományt.
- kapcsolatszerkesztő
A különböző forrásokból származó tárgykódok összeszerkesztésére szolgál. Létrehozza a futtatható állományt.
- kettes komplemens
Egy bitsorozaton végzett művelet, mely során annak egyes komplemenséhez binárisan hozzáadunk
1-et. Például az10011000kettes komplemense a01101000.- kettes számrendszer
A numerikus értékek olyan megjelenítési formája, ahol kizárólag kétféle számjegyet használhatunk. Ezek a
0és az1.- kódolás
Adatok és bitkombinációk egyértelmű egymáshoz rendelése. Segítségével minden számítógépen tárolandó dolgot
0-ák és1-esek sorozatává tudunk alakítani. A visszaalakítás, vagyis a dekódolás is egyértelmű kell legyen.- magas szintű programozási nyelv
A programozási nyelvek harmadik generációjába tartozó nyelvek csoportja. Jóval absztraktabb, mint a korábbi assembly programozás. Ide tartozik például a C, a C++, a C#, a Java és a Python nyelv is.
- megjegyzés
A program forráskódjának egy kiegészítése, mely nem befolyásolja a végrehajtás mentét, de hasznosak lehetnek a programozó számára, segíthetik a kód könnyebb megértését.
- posztfix kifejezés
A kifejezések egyik egyértelmű megjelenési formája, amelyben a kétoperandusú operátorok mindig az operandusaik után helyezkednek el.
- prefix kifejezés
Kifejezések megadásának egyik egyértelmű módja, ahol az operátorok mindig megelőzik az operandusaikat.
- számábrázolás
Numerikus értékek felírási módja adott darabszámú bit segítségével. Például egész számok esetén alkalmazhatjuk a fixpontos számábrázolást, törtek esetén pedig a lebegőpontos számábrázolást.
- szemantika
Egy program értelmezése, jelentése. Azt határozza meg, mire szolgál, és hogyan működik egy program. A program által használt algoritmus határozza meg.
- szemantikai hiba
A program (algoritmus) írása során vétett hiba, amely miatt az máshogy fog működni, mint ahogy terveztük.
- szintaktikai hiba
Programozói hiba, amely akkor keletkezik, ha nem tartjuk be az adott nyelv szintaxisát/szintaktikáját (például elgépelünk valamit).
- szintaxis
Egy adott programozási nyelv formai és tartalmi szabályrendszere, ami meghatározza, milyen eszközt hogyan használhatunk az adott nyelven írt forráskódban. Egy nyelv szintaxisának ismerete egyik (de nem az egyetlen) előfeltétele annak, hogy azon a nyelven képesek legyünk működőképes program megírására.
- tárgykód
Fordítóprogramos nyelvek esetén a forráskódból generált állomány, mely bár közel áll a gépi kódhoz, önmagában nem futtatható.
- típus
Adatok általános jellemzője, amely meghatározza az adat tárolásának módját és korlátait, valamint a rajtuk elvégezhető műveletek halmazát.
- tizenhatos számrendszer
A numerikus értékek olyan megjelenítési formája, ahol összesen 16 féle különböző számjegyet használhatunk. Ezek rendre a következők:
0,1,2,3,4,5,6,7,8,9,A,B,C,D,EésF.- tizes számrendszer
A számok szokásos megjelenítési formája, ahol kizárólag 10 féle számjegyet használhatunk.
8.4. Kérdések, feladatok¶
Ha már ismersz valós programozási nyelveket, akkor tudd meg, hogy azok a programozási nyelvek melyik osztályába tartoznak!
Tegyük fel, hogy az alábbi pszeudokód a
Bszámot az természetes számként megadottEkitevőre emeli és kiírja a hatvány értékét. Keress a kódban szintaktikai és szemantikai hibákat! [S802]1 2 3 4 5 6 7
input B P=0 wihle E<=0 P=P*B E-1=E endo output P
Mennyi az értéke az alábbi prefix kifejezéseknek? [S803]
+ 103 - / * 6 35 14 7 - - - 900 1000 3 20
Mennyi az értéke az alábbi posztfix kifejezéseknek?
24 6 / 2 3 * + 10 - 42 35 10 12 6 / / / /
Alakítsd át az alábbi prefix kifejezést infixé!
* + 20 10 - 20 10
Alakítsd át az alábbi posztfix kifejezést infixé! [S806]
1 3 4 * 1 2 + / 103 97 - * +
Alakítsd át az alábbi infix kifejezéseket posztfixé és prefixé is!
1 + 2 * 3 + 4 (1 + 2) * (3 + 4) 1 + 2 * (3 + 4) (1 + 2) * 3 + 4
Egy interpreteres nyelven írt tetszőleges program forráskódja vagy tárgykódja hosszabb?
Az integrált fejlesztői környezetek automatikusan fel tudják hívni a programozó figyelmét a szemantikai hibákra? [S809]
Melyik a következő egész szám kettes számrendszerben a
110100101111után?Váltsd át kettes számrendszerbe a következő decimális számokat:
64;63;0,1;-25,25!Váltsd át tízes számrendszerbe a következő bináris számokat:
10000;1111;0,1;-1011010,0101!Váltsd át kettes számrendszerbe a következő hexadecimális számokat:
123;7F;BAD!Váltsd át tizenhatos számrendszerbe a következő bináris számokat:
011001100110;1010111010;1111111011101101!Mennyi az összege a
10010011és111010bináris számoknak?Végezd el a
10001és a110szorzását kettes számrendszerben! [S816]Hány különböző bitkombinációt tudsz felírni 4 biten és 10 biten?
Minimálisan hány bitet használnál 30 különböző dolog kódolására?
Két bájton egyértelműen kódolhatjuk-e a Föld népességét? [S819]
Add egy a
01110110bitsorozat egyes majd kettes komplemensét!Mi az a 32 bit, amely előjeles fixpontos számábrázolás esetén a
-1értéket képviseli? [S821]Ábrázold a
+3,5értéket egyszeres pontosságú (4 bájtos) lebegőpontos számábrázolással! [S822]Mit gondolsz, típusokat használó programozási nyelv esetén egy változó bármilyen értéket felvehet? [S823]