9. Megoldások

A korábbi fejezetekben található néhány kérdésre és feladatra vonatkozóan itt megtalálhatod a válaszokat és a megoldásokat. Az itt található megoldások az azonosító kóddal megjelölt feladatokhoz tartoznak. Kérlek, először önállóan próbálkozz a megoldással és ezt a fejezetet csak ellenőrzésre használd!

9.1. A problémamegoldás és a számítógép

[S102]:

• Fájl megnyitás és mentés

• Képformátumok kezelése

• Vágólap kezelés

• Színkeverés

• Rajzeszközök (ceruza, ecset, radír, kitöltés, stb.) használata

• Alakzat beszúrás

• Képtranszformációk (átméretezés, forgatás, tükrözés, stb.)

• Beállítások

9.2. Az algoritmusokról általában

[S202]:

• Nem félreérthetetlen: Mit jelent a „közelítőleg megegyezik”?

• Nem véges: Ha A>B, akkor a különbség folyton nőni fog. Ha az elején nem áll meg az algoritmus, akkor a később sem. Tegyük fel, a „közelítőleg megegyezik” kifejezés matematikai egyenlőséget jelent és B>A. Ekkor ha B-A páros, akkor az algoritmus jól működik, különben viszont nem áll meg ismét.

9.3. A folyamatábra

[S301]:

Ha egy rombusz (feltétel) két oldaláról kiinduló ágak találkoznak és a csatlakozási pontból csak egy nyíl megy tovább, akkor a feltétel egy elágazáshoz tartozik. Amennyiben a rombuszból kiinduló egyik végrehajtási ág visszavezet közvetlenül a rombuszhoz (míg a másik ág nem), akkor a feltétel egy ciklus feltétele.

[S302]:

x	y
60	?
60	2
30	2
15	2
15	3
5	3
5	4
5	5
1	5

A kimenet: 2 2 3 5.

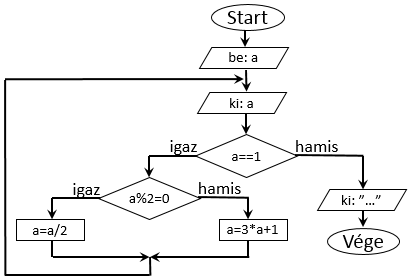
[S309]:

9.4. A pszeudokód

[S403]:

A kimeneten a 15 lesz, mivel az output utasítás a bemenetként megadott két egész szám legnagyobb közös osztóját írja ki. Ezt az algoritmust Euklideszi algoritmusnak hívják.

[S404]:

Az algoritmus a bementként (tízes számrendszerben) megadott természetes számot kettes számrendszerbeli alakra hozza.

   input N
   P = 1
   R = 0
   while N>0 do
     R = R+(N%2)*P
     N = (N-N%2)/2
     P = P*10
   enddo
   output R

[S405]:

Az algoritmus a bementként megadott természetes számot prím tényezőkre bontja. Ezek a prímszámok lesznek a kimeneten.

   input x
   y = 2
   while y<=x do
     if x%y==0 then
       output y
       x = x/y
     else
       y = y+1
     endif
   enddo

[S408]:

   input a, b, c
   if a*a+b*b==c*c OR b*b+c*c==a*a OR c*c+a*a==b*b then
     output "Derékszögű háromszög."
   else
     output "Nem derékszögű háromszög."
   endif

Egy hosszabb alternatív megoldás így nézhet ki egymásba ágyazott elágazásokkal.

   input a, b, c
   if a*a+b*b!=c*c then
     if b*b+c*c!=a*a then
       if c*c+a*a!=b*b then
         output "Nem derékszögű háromszög."
       else
         output "Derékszögű háromszög."
       endif
     else
       output "Derékszögű háromszög."
     endif
   else
     output "Derékszögű háromszög."
   endif

[S410]:

   input N
   S = 2
   while S*S<=N AND N%S!=0 do
     S = S+1
   enddo
   if N%S==0 then
     output ”Nem prím.”
   else
     output ”Ez egy prím.”
   endif

[S412]:

Az alábbi megoldásban nem tároljuk folyamatosan az összes elemet, mivel úgyis mindig csak a két legutóbbira kell emlékeznünk. Az újonnan kiszámolt értéket mindig csak a következő két lépésben kell ismernünk.

   F1 = 0
   F2 = 1
   output F1, F2
   N = 2
   while N<20 do
     F3 = F1+F2
     output F3
     N = N+1
     F1 = F2
     F2 = F3
   enddo

9.5. Tömbök

[S504]:

Mivel 11 lehetséges elemünk van ezért egy 11 elemű tömbben (Times) megszámoljuk, melyik értékből mennyi van. Ennek a tömbnek legnagyobb értékű elemének indexe határozza meg a leggyakoribb elemet.

   i = 0
   while i<11 do
     Times[i] = 0
     i = i+1
   enddo
   i = 0
   while i<N do
     Times[A[i]-10] = Times[A[i]-10]+1
     i = i+1
   enddo
   max = 0
   i = 1
   while i<11 do
     if Times[i]>Times[max] then
       max = i
     endif
     i = i+1
   enddo
   output "A leggyakoribb elem a ", max+10
   output "Ez ", Times[max], " alkalommal fordult elő."

[S509]:

A tömböt logikailag két változó méretű részre osztjuk. A tömb elejét egy rendezett résztömbnek képzeljük el, kezdetben egy, majd egyre több elemmel. A tömb hátralévő része marad az eredeti rendezetlen formában. Minden lépésben a rendezetlen szakasz első elemét szúrjuk be a rendezett rész megfelelő helyére a nagyobb értékek eggyel hátrébb csúsztatása közben. Ezzel egy elemmel bővül a rendezett szakasz. Ezt a lépést kell megfelelő számban ismételni.

   actual = 1
   while actual<N do
     i = actual-1
     while A[i]>A[i+1] AND i>=0 do
       tmp = A[i+1]
       A[i+1] = A[i]
       A[i] = tmp
       i = i-1
     enddo
   actual = actual+1
   enddo

[S511]:

Mind a két eredeti tömbnek és az új tömbnek is az elejéről indulunk. Amelyik aktuális elem kisebb az eredeti tömbökben, azt átmásoljuk az új tömb aktuális pozíciójába és ezen az elemen átlépünk mind a két tömbben. Ezt addig folytatjuk, amíg valamelyik eredeti tömb végét el nem érjük, majd a másik tömb maradék elemeit is átmásoljuk.

   iA = 0
   iB = 0
   iC = 0
   while iA<N AND iB<M do
     if A[iA]<B[iB] then
       C[iC] = A[iA]
       iA = iA+1
     else
       C[iC] = B[iB]
       iB = iB+1
     endif
     iC = iC+1
   enddo
   if iA==N then
     while iB<M do
       C[iC] = B[iB]
       iB = iB+1
       iC = iC+1
     enddo
   else
     while iA<N do
       C[iC] = A[iA]
       iA = iA+1
       iC = iC+1
     enddo
   endif

9.6. Alprogramok

[S602]:

• Az algoritmus 1-től a bementként megadott számig (Max) minden természetes számot kétszer kiír a kimenetre.

• A függvényhívások száma függ a bemenet értékétől. Ha Max értéke 0, akkor egyszer sem hívódik meg, ha a bemenet egy pozitív egész szám, akkor Max*2-1 alkalommal hívódik meg. Összességében tehát azt mondhatjuk, hogy egész értékű bemenet esetén maximum{0 ; Max*2-1} függvényhívás történik.

• A függvényt most mindig 0 vagy 1 aktuális paraméter értékkel hívtuk meg és ekkor rendre 1 és 0 értékeket ad vissza. Tehát a függvényt most arra használtuk, hogy két állapot között ide-oda váltogasson.

[S604]:

Dupla ciklust alkalmazva sorokba és oszlopokba rendezett értékeket íratunk ki. Új sort az output NEWLINE utasítással tudunk létrehozni. Egy soron belül egy adott érték kiírása után átváltunk a másik értékre. Ha az oszlopok elemszáma (N) páros, akkor ugyanazt az értéket kell kiírni egy sor végére, mint a következő elejére. Páratlan oszlopszám páratlan, akkor soremelésnél is váltani kell a kiírandó értéket.

   procedure chessboard( N )
     V = 0
     i = 1
     while i<=N do
       j = 0
       while j<=N do
         output V
         V = 1-V
         j = j+1
       enddo
       if N%2==0 then
         V = 1-V
       endif
       output NEWLINE
       i = i+1
     enddo
   end procedure
   output "Add meg a méretet! "
   input S
   call chessboard( M )

[S608]:

A hatványozás megadható megfelelő számú szorzás alkalmazásával nullánál nagyobb, egész kitevő esetén. Ezt egy ciklussal megoldhatjuk. A negatív kitevő esetén a pozitív kitevőjű hatvány reciprokát kell megadnunk. Az alábbi megoldásban a függvényt négyszer is meghívjuk különböző paraméterekkel. A kimenetek: 32  0.001  1  0.04

   function power( B, E )
     P = 1
     if E<0 then
       E = -1*E
       N = 1
     endif
     while E>0 do
       P = P*B
       E = E-1
     enddo
     if N==1 then
       P = 1/P
     endif
     return P
   end function
   output power( 2, 5 )
   output power( 0.1, 3 )
   output power( 321, 0 )
   output power( 5, -2 )

[S611]:

Egy teljes keresést valósítunk meg a függvényben őrszem használatával. Feltételezzük, hogy az A nevű, N elemű több már fel van töltve értékekkel. A visszatérési értéket nem íratjuk ki, de a példa kedvéért felhasználjuk.

   function keres( B, M, Y )
     B[N] = Y
     i = 0
     while B[i]!=Y do
     i = i+1
     enddo
     if i==M then
       return -1
     else
       return i
     endif
   end function
   output "Mit keresel?"
   input X
   i = keres( A, N, X )
   if i==-1 then
     output "Nincs szerencséd."
   else
     if i<N/2 then
       output "Az elem a tömb első felében van."
     else
       output "Az elem a tömb második felében van."
     endif
   endif

[S614]:

Vegyük észre, hogy az eljárás meghívódhat a saját törzsén belül is, azaz rekurzióról beszélhetünk. A végrehajtás a 11. sorral kezdődik, ahol tehát N értéke 900 lesz. A 12. sorban először hívódik meg az eljárás, ha majd ez befejeződik, akkor a 13. sorral fogjuk folytatni. Az első hívás során a 900 és a 2, mint aktuális paraméter értékek átmásolódnak az x és y formális paraméterekbe. (Az eljárás első példányában tehát x=900 és y=2.) Az első és a második elágazás feltétele is teljesül, tehát végrehajtjuk a 4. sort, azaz meghívjuk a foo eljárást ismét, csak most a 450 és 2 aktuális paraméterekkel. Ez a két érték a második hívás x és y változójába kerül. (Ha majd kész leszünk ezzel a második hívással, akkor majd az 5. sorral folytatjuk.) A feltételek teljesülése miatt újra a 4. sorban vagyunk, azaz harmadjára is meghívjuk a eljárást (foo( 225, 2 )). Ebben a példányban a második elágazás feltétele hamisnak bizonyul, így az else ágra ugrunk, ahol megtörténik a negyedik hívás is (aktuális paraméterek: 225 és 3). Ha majd egyszer visszatérünk ide, akkor utána a 8. sor fog következni. Ha folytatjuk ezt a gondolatmenetet, néhány további hívás után, az egyik eljárás példány 2. sorában az elágazás feltétele hamis lesz és mivel nincs else ág így az eljárás be is fejeződik. Visszatérünk az előző példány 5. sorába, kiírva a kilencedik eljárás példány y változójának értékét vagyis, az 5-öt. Ezután vége az elágazásoknak és így ennek a példánynak is. Visszatérünk a 8. példány 5. sorába. Itt egy újabb 5-ös kiírása után ismét befejeződnek az elágazások és a 8. példányból visszatérünk a 7. példány 7. sorába. Előbb-utóbb a legelső eljárás is véget ér, visszatérünk a főprogram 13. sorába.

A helyzet könnyebb átlátása érdekében tekintsük át az alábbi táblázatot, amely az egyes eljáráshívások adatait tartalmazza.

hívás	hívó	első paraméter	második paraméter	hívás helye
	főprogram	900	2	sor
	az 1. eljárás példány	450	2	sor
	a 2. eljárás példány	225	2	sor
	a 3. eljárás példány	225	3	sor
	a 4. eljárás példány	75	3	sor
	az 5. eljárás példány	25	3	sor
	a 6. eljárás példány	25	4	sor
	a 7. eljárás példány	25	5	sor
	a 8. eljárás példány	5	5	sor
	a 9. eljárás példány	1	5	sor

Tíz alkalommal történt tehát az eljárás meghívás a rekurziónak köszönhetően. Egyszer a 12. sorban, hatszor a 4. sorban és háromszor a 7. sorban. A végrehajtás során az alábbi kimenet keletkezik.

5 5 3 3 2 2

Mint látható ez az eredeti paraméter prím tényezős felbontása, mivel 900 = 5*5*3*3*2*2.

9.7. Tesztelés

[S702]:

Az algoritmus N értéke kizárólag természetes szám lehet, a B változó pedig a { 2, 3, 4, 5, 6, 7, 8, 9, 10 } halmaz elemeit veheti fel, más bemenetek esetén elvileg sem ad helyes kimenetet. Egy lehetséges tesztkészletet tartalmaz a következő táblázat.

N	B	Elvárt kimenet
0	2	0
1	2	0
11	2	1011
12	2	1100
32	2	10000
31	2	11111
1000000000	2	111011100110101100101000000000
11	3	102
12	3	110
7	4	13
8	4	20
24	5	44
25	5	100
15	6	23
342	7	666
0	8	0
7	8	7
8	8	10
9	8	11
1000000000	8	7346545000
39	9	43
0	10	0
5	10	5
25	10	25
125	10	125

9.8. Implementáció

[S802]:

Szintaktikai hibák:

• A while szó helyett wihle szerepel.

• A ciklus feltétele után nincs do kulcsszó.

• Az értékadás bal oldalán mindig csak egy változó szerepelhet. E = E-1 a helyes.

• Az endo egy azonosító lehet (nem kulcsszó). A ciklust enddo kulcszóval kell zárni. (Most nincs ciklusvég.)

Szemantikai hibák:

• Az E kezdőértéke ismeretlen. Bemenetként kellene megadni. Hiányzik a pszeudokód elejéről egy input E utasítás.

• Az R kezdőértékének nem jó választás a nulla, mivel az R = R*B utasításnak így nincs hatása. Mivel ebben az utasításban szorzás szerepel, a valós számok multiplikatív egységelemére van szükségünk az additív helyett. Helyesen R = 1.

• Ha a ciklus magja akkor is lefut, amikor az E értéke nulla, akkor eggyel nagyobb kitevőjű hatvány lesz az eredmény. A feladat leírása szerint az algoritmusnak negatív kitevőt (E<0) nem kell kezelnie. A feltételnek E>0 logikai kifejezésnek kell lennie.

[S803]:

Az első kifejezés értéke 109, a másodiké -123. A kiértékelés menete a következő:

+ 103 - / * 6 35 14 7
+ 103 - / 210 14 7
+ 103 - 13 7
+ 103 6
109

- - - 900 1000 3 20
- - -100 3 20
- -103 20
-123

[S806]:

A megoldás előbb teljesen zárójelezett formában, majd pedig a felesleges zárójelek elhagyása után így néz ki:

( 1 + ( ( ( 3 * 4 ) / ( 1 + 2 ) ) * ( 103 - 97 ) ) )
1 + 3 * 4 / ( 1 - 2 ) * ( 103 - 97 )

[S809]:

A szemantikai hibák nem formalizálhatóak. A szemantikai hibát tartalmazó program is végez tevékenységeket, csak az eredmény nem az, amit a programozó szeretett volna. Ha a számítógép minden esetben felismerné, hogy mit akart a programozó, akkor nem lenne szükség programozóra. Az IDE-k nem ismerik fel a szemantikai hibákat.

[S816]:

A szorzás menete ugyanaz, mint hagyományosan tízes számrendszerben, csak összesen kétféle számjegyünk van. Emiatt a szorzótábla és az összeadás is jóval egyszerűbb. Az eredmény 1100110 (mivel decimálisan 17*6=102). A számolás menetét az ábra mutatja.

[S819]:

A két bájt az 16 bitet jelent. Összesen 65536 különböző kettes számrendszerbeli természetes szám van, amely nem hosszabb 16 helyiértéknél. Vagyis 2^16 darab eltérő értéket tudunk tárolni 0-tól 65535-ig. A Föld lakosainak száma jelenleg közel 8 milliárd, ami jelentősen magasabb érték, mint az előbb említett maximum, így nem tudjuk ezt a számot 2 bájton eltárolni. (Megjegyzés: még 4 bájton sem lehetséges.)

[S821]:

A -1 negatív szám, előjeles fixpontos számábrázolással tárolhatjuk, amihez a kettes komplemens képzés technikáját kell alkalmaznunk. Vegyük a szám abszolút értékét és írjuk fel kettes számrendszerben 32 biten! Ezt kapjuk: 00000000000000000000000000000001. Ennek az egyes komplemense az 11111111111111111111111111111110. Ha ehhez hozzáadunk egyet, megkapjuk a kettes komplemenst, tehát az eredmény: 11111111111111111111111111111111, azaz 32 darab 1-es bit. Mint látható a legelső (előjel) bit 1-es, vagyis a szám tényleg negatív.

[S822]:

Az adott szám pozitív tehát a legelső bit biztosan 0 lesz. Ha átváltjuk a 3,5 értéket kettes számrendszerbe, akkor 11,1 bináris értéket kapunk. Hozzuk normál alakra, azaz toljuk el a kettedes vesszőt az első 1 bit elé! Az eredmény 1,11, amelyet tehát a kettedes vessző 1 helyiértékkel való balra tolásával kaptunk. Ehhez az 1-hez adjunk hozzá 127-et! Az eredmény 8 biten a 10000000 lesz, vagyis ez a következő 8 bitje a reprezentációnak. Ezt követi a mantissza (jelenleg 1,11) kettedes vessző utáni része 0 bitekkel kiegészítve. Az eredmény tehát logikai illetve bájtonkénti tagolásban a következő:

0 10000000 11000000000000000000000
01000000 01100000 00000000 00000000

Ez a 32 bit jelenti a +3,5 értéket egyszeres pontosságú lebegőpontos számábrázolás esetén.

[S823]:

Típusos nyelvekben egy változó nem vehet fel tetszőleges értéket. A típus egyértelműen meghatározza a lehetséges értékek halmazát. Természetesen egy előjel nélküli egész típusú változó értéke nem lehet -123, egy egész típusú változó nem tárolhatja a 3,14 értéket és egy valós típusú változó értéke nem lehet az „Euler-szám” karaktersorozat. Ezen túlmenően logikailag megfelelő típusú értékek sem biztos, hogy tárolhatóak a technikai korlátok miatt. A legtöbb nyelv egész típusú változója képtelen eltárolni a például a tízmilliárdot (mert túl nagy) vagy a valós típusú változóik a 0,1 értéket csak pontatlanul tudják eltárolni (mivel ez binárisan egy végtelen kettedes tört).