4. A pszeudokód

Amíg a folyamatábra az algoritmusok egy grafikus megjelenítési formája, addig a pszeudokód egy szöveges leírás. Külalakját tekintve nagyon hasonló a valós programnyelvek forráskódjához, bár egyértelműen eltér azoktól. Gyakran azt mondjuk, félúton van a mondatszerű leírás és a valós magas szintű programnyelvek között. Számos jól definiált jelentéssel bíró ún. kulcsszó-t alkalmaz, például az algoritmus alapszerkezetek megadásához. Tekintsük át ezeket!

Az egyes elemi utasításokat külön sorokba írjuk. A szekvencia emiatt nem más, mint egymás alatti sorokban megadott utasítások. Egy programegység utasításainak végrehajtását mindig az első (legfelső) sorával kezdjük, majd ezután az alatta lévő sor utasítással folytatjuk és így tovább. A felírás sorrendjének tehát fontos szerepe van.

Az elágazás megadásához kulcsszavakat más néven lefoglalt szavakat használunk. Az elágazást mindig egy if kulcsszóval vezetjük be a sor elején. Jelentése: ha. Ezután egy feltételt fogalmazunk meg egy logikai kifejezés segítségével. Ezt egy then (azaz akkor) kulcsszó követi, tehát a feltétel mindig az if és then kulcsszópár között van megadva általában egy sorban. Az ez utáni sor(ok)ban kell megadni az elágazás igaz ágát, vagyis azokat az utasításokat szekvenciálisan, amelyeket igaz feltétel esetén szeretnénk végrehajtani. Ezt az utasításcsoportot egy újabb sorban megadott else kulcsszó zárja általános esetben. Az else kulcsszó egyben a hamis ág kezdetét is jelenti, tehát utána találjuk a hamis feltétel esetén végrehajtandó utasítások sorait. Végül a szerkezetet az endif kulcsszó zárja. Ez a kulcsszó azért fontos, mert így mindig tudjuk, hogy melyik utasítás tartozik az adott feltételes ágba és melyik az, amely az elágazáson kívüli mindenképpen végrehajtandó lépés. Mint korábban már említettük az elágazások hamis ága elhagyható, ilyenkor a then kulcsszó utáni igaz ágat közvetlenül az endif követi. Általános esetben tehát így néz ki a teljes elágazás:

1
2
3
4
5
   if <feltétel> then
     <utasítások>
   else
     <utasítások>
   endif

A végrehajtás menetet pedig a következőképpen írható le:

  1. Értékelt ki a feltételt, azaz dönts az igazságtartalmáról!

  2. Amennyiben a feltétel igaznak bizonyul hajtsd végre szekvenciálisan a then és az else kulcsszó közötti utasításokat, majd folytasd a 4. lépéssel!

  3. Különben (hamis feltétel esetén), hajtsd végre az else és az endif közötti utasításokat!

  4. Folytasd a végrehajtást az elágazást követő utasítással, amit az endif utáni sorban találsz!

A hamis ág nélküli elágazás szerkezete a következő:

1
2
3
   if <feltétel> then
     <utasítások>
   endif

Ebben az esetben, ha a feltétel hamisnak bizonyul, akkor az endif kulcsszót követő sorban lévő utasítást hajtjuk végre, kihagyva az igaz ágat a végrehajtásból. Fontos hangsúlyozni, hogy csak a hamis ág elhagyható pszeudokódban, az igaz ág mindig jelen kell legyen.

Egy ismételés megadása a while (vagyis amíg) kulcsszóval kezdődik, amit egy feltétel követ, majd a sort a do foglalt szó zárja. Az ez utáni sor(ok)ban található a ciklus magja egészen az enddo kulcsszót tartalmazó sorig. Az általános forma tehát ez:

1
2
3
   while <feltétel> do
     <utasítások>
   enddo

Miután a while előtti sort befejeztük, kiértékeljük a feltételt. Ha ez igaz, akkor belépve a ciklusmagba végrehajtjuk a do és az enddo közötti utasításokat. Ezt ciklikusan a feltétel újbóli kiértékelése követi, hasonlóan az előzőekhez. A pszeudokód ciklusa tehát igaz-ra ismétel. Amennyiben a feltétel bármikor (akár már az első kiértékelés során) hamisnak bizonyul a ciklusmag kihagyásával az enddo utáni sor végrehajtásába kezdünk.

A további pszeudokód kulcsszavak közül két gyakran használt kulcsszót kell még itt megemlítenünk, melyek az I/O műveleteket jelenítik meg. Adatbekéréshez az input kulcsszóval kezdődő bemeneti utasítást használjuk, amelyet egy változónév (esetleg változónevek listája) követ, ahová a kapott adatok elmentésre kerülnek. A felhasználó felé történő kimenet megadására az output kulcsszó utáni kifejezés megadásával történik. Ha például a felhasználó által méterben megadott hosszúságértéket centiméter egységben akarjuk kiíratni, akkor csak az alábbi két sort tartalmazó szekvenciális pszeudokódot kell megadnunk:

1
2
   input HOSSZ_METERBEN
   output 100*HOSSZ_METERBEN

Egy utasításban több dolgot is beolvashatunk vagy kiírhatunk. Kiíratásnál az egyszerű szöveges üzenet esetén a szöveget idézőjelbe kell tenni.

1
2
3
   output "Add meg a pontos időt (óra:perc)!"
   input ORA, PERC
   output "Ma eddig ", ORA*60+PERC, " perc telt el."

A kimenet tehát így fog kinézni egy konkrét esetben:

Add meg a pontos időt (óra:perc)!
6:10
Ma eddig 370 perc telt el.

4.1. Indentálás

Meg kell még említeni egy technikát, aminek használata nem kötelező, de javítja a kód olvashatóságát így használata erősen ajánlott. Ez az úgynevezett indentálás. Alap esetben írhatjuk a kód minden utasítását a sor legelejére. Szemléletesebb lesz viszont a kód, ha az algoritmus logikai szerkezetét a kód külső megjelenése is tükrözi. Például, ha egy utasítás egy elágazás egyik ágában vagy egy ciklus magjában helyezkedik el, akkor érdemes ezt az utasítást nem a sor elején kezdeni, kicsit bentebb húzva ezt az utasítást. Egy pszeudokódban többszörös egymásba ágyazás is előfordulhat, amikor például egy ciklus magjában van egy elágazás, amely akár egy másik elágazást vagy ciklust is tartalmazhat. Láttunk már ilyet az előző fejezetben, amikor a szökőév meghatározó folyamatábrát alkottuk meg. Lássuk most ugyanazt az algoritmust indentált pszeudokód segítségével.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
   input ev
   if ev%4==0 then
     if ev%100==0 then
       if ev%400==0 then
         output "igen"
       else
         output "nem"
       endif
     else
       output "igen"
     endif
   else
     output "nem"
   endif

Az indentálás révén könnyen azonosíthatja az olvasó az egymást tartalmazó szerkezeteket. Minden tartalmazott egység kissé be van húzva az őt tartalmazó egységhez képest.

Meg kell jegyeznem, hogy az előző pszeudokódban (és később minden továbbiban) lévő logikai kifejezésekben az == alternatív jelölést használom az értékek egyenlőségének vizsgálatára. Ezzel is kihangsúlyozva két művelet eltérő jelentését. Az A=B utasítás egy értékadást jelöl, jelentése: tárold el a B mennyiség értékét az A változóba! Az A==B kifejezés azt jelenti, döntsd el, hogy A és B értéke megegyezik-e! Később a valós nyelvekben is megfigyelhető lesz ez az eltérő jelölés.

4.2. A pszeudokód és a folyamatábra megfeleltetése

A fentiek alapján egy algoritmus konvertálása folyamatábrából pszeudokódra vagy ellenkező irányban könnyen elvégezhető. Néhány speciális esetre, szabályszerűségre, különbségre azért érdemes felhívni a figyelmet.

  • Pszeudokódban nincs Start szimbólum. A végrehajtás az első sorral kezdődik. (Később ez az állítás egy kis korrekcióra szorul majd.)

  • A Vége szimbólum nem szükséges pszeudokódban, ha elfogynak a sorok a végrehajtás befejeződik. (Egyes esetekben praktikus lehet a végrehajtás megállítása az utolsó sornál hamarabb. Szükség esetén használhatjuk a stop kulcsszót.)

  • A végrehajtás menetét alapvetően a felírás sorrendje határozza meg pszeudokódban, míg folyamatábra esetén ezt a szerepet a nyilat töltik be.

  • A folyamatábra téglalapjaiban szövegesen megadott elemi lépéseket pszeudokódban csak egyszerűen egy külön sorban tüntetjük fel.

  • A paralelogramma szimbólumok szerepét pszeudokódban az input/output utasítások veszik át.

  • Folyamatábra esetén a feltételek vannak jelölve (rombusz) nem az elágazás vagy az iteráció maga. Emiatt a leképezésnél könnyen összezavarodhatunk. Ha egy rombuszból kiinduló egyik nyíl mentén haladva visszajuthatunk közvetlenül a rombuszhoz (enddo), akkor ismétlésről van szó, azaz pszeudokódban a while kulcsszó után kell írni a feltételt (a rombusz tartalmát). Ha a rombuszt elhagyó nyilak mentén haladva a két ág egyesül, azaz két nyíl egybeolvad (endif), akkor a rombusz tartalmát az if és a then kulcsszó közzé írjuk.

  • Szükség esetén egy folyamatábra ágainak címkéi (igaz vagy hamis) felcserélhetőek a feltétel tagadásával.

  • Ismétlés esetén az (jobb esetben igaz címkével ellátott) visszatérő ág kerül a do és az enddo közzé. Az általában hamis címkével ellátott magelkerülő ág utasításait egyszerűen az enddo után írjuk.

  • Elágazás esetén az utasításokat mindenképpen tartalmazó (általában igaz címkével ellátott) ág utasításai a then kulcsszó után kell, hogy elhelyezkedjenek. Amennyiben az egyik ág nem tartalmaz utasításokat, akkor pszeudokódban kihagyjuk az else kulcsszót.

  • A while, a do és az enddo kulcsszavak mindig együtt (azonos számban) fordulnak elő.

  • Az if, a then, az else és az endif kulcsszavak mindig együtt fordulnak elő. Előfordulásuk száma (az else kivételével) mindig megegyezik, egy adott kódban az else-ek száma lehet kevesebb is, mint az if-eké.

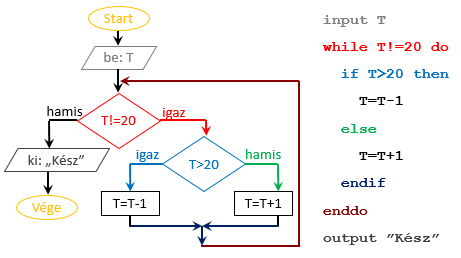
A felsorolás elemeit szem előtt tartva könnyen átkonvertálhatunk egy algoritmust a két megjelenítési módszer között. Az alábbi ábra számos elem megfeleltetését mutatja be különböző színekkel megjelenítve őket.

Folyamatábra és pszeudokód megfeleltetés

4.3. További példák pszeudokódra

Azért hogy jobban megértsük a pszeudokóddal megadott algoritmusok működését illetve, hogy jobban átlássuk a kód megírásának folyamatát három további problémát is megoldunk.

1. példa: Először próbáljunk meg értelmezni egy már kész pszeudokódot! Vizsgáljuk meg mikor, milyen értéket vesznek fel a benne szereplő változók. Az algoritmus bemenetéről tudjuk, hogy két pozitív egész számról van szó. Az algoritmus a következőképpen néz ki:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
   input A
   input B
   while A!=B do
     if A>B then
        A = A-B
     else
        B = B-A
     endif
   enddo
   output B

Hajtsuk végre az algoritmust követve a pszeudokódban megadott utasításokat! Először meg kell adnunk a két bemeneti értéket. Legyenek ezek, mondjuk a 24 és a 18! A két érték elmentődik tehát a megadott változókba (A=24, B=18). Ezután egy ciklus következik, aminek a feltételét kell kiértékelnünk. Most az A és a B változó értéke nem egyenlő, azaz a feltétel igaz. Végre kell hajtanunk a ciklus magját. Itt az első lépés egy elágazás feltételének megvizsgálása. Mivel 24 nagyobb, mint 18, így a feltétel igaz, azaz a then és az else kulcsszavak közötti utasítást kell végrehajtani. Először az értékadás jobb oldalán lévő kifejezés értékét határozzuk meg. A két változó értékének különbsége 6, amit az értékadás bal oldalán megadott A változóban tárolunk el (felülírva a korábban ott tárol 24 értéket). Tehát jelenleg A=6 és B=18. Mivel az else ágat ki kell hagyni, a ciklusmagban már nincs már utasítás. Az enddo azt jelenti, hogy vissza kell mennünk a ciklus feltételéhez és újra megvizsgálni azt. A második kiértékelés is igaz feltételt jelent, a ciklusmagot újra végre kell hajtani. Az elágazás feltétele most hamis, mivel a 6 nem nagyobb, mint a 18. Az else kulcsszóra kell ugranunk, majd a B változó értékét megváltoztatni 12-re. Ismét vissza kell ugranunk a ciklus feltételhez, ami még mindig igaz. Harmadjára is belépve a ciklusba az if feltétele most éppen 6>12 az A értéke most változatlan marad B viszont ezentúl a 6 értéket fogja tárolni. Az enddo révén ismét visszajutunk a ciklusfeltételhez. Ebben az esetben viszont már mindkét változó értéke 6, vagyis az egyenlőtlenség nem teljesül. Amikor a while feltétele hamis nem lépünk be a ciklusba, hanem az enddo utáni következő utasítást hajtjuk végre. Ez a B változó értékének megjelenítését eredményezi, aktuálisan tehát a kimenet a felhasználó felé a 6 érték.

Hajtsuk még végre többször is a fenti algoritmust különböző bemenetek esetén és jegyezzük fel milyen bemenetek esetén milyen kimenetet kapunk!

Bemenetek

Kimenet

24

18

6

18

24

6

13

13

13

55

45

5

11

7

1

136

272

136

Ha megvizsgáljuk mi az összefüggés a bemeneti értékek és a kimenet között, akkor rájöhetünk arra is, hogy mit csinál az algoritmus. Az A és B pozitív egész számok legnagyobb közös osztóját határozhatjuk meg vele.

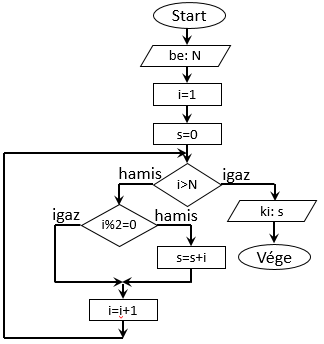
2. példa: Szeretnénk tudni, hogy egy adott egész számnál nem nagyobb, pozitív, páratlan számok összege mennyi. Ehhez elkészítettünk egy algoritmust folyamatábra segítségével. Most szeretnénk ugyanezt az algoritmust pszeudokóddal megadni.

Az algoritmus folyamatábrája

Ez első lépések leképezése egyszerűen az alábbi 3 pszeudokód sort eredményezi:

1
2
3
   input N
   i = 1
   s = 0

Ezután egy rombuszt, azaz feltételt találunk, tehát először ki kell derítenünk, vajon ciklusról vagy elágazásról van szó. Mivel a feltétel bal oldalán haladva újra eljuthatunk közvetlenül a feltétel elé így egyértelműen ciklusról van szó. Ez egyben azt is jelenti, hogy a bal ágban van a ciklus magja. Ez viszont a hamis címkével ellátott ág. Egy while ciklus mindig igaz feltétel esetén ismétlődik (hamis esetben kell kilépnünk a ciklusból). Ezt az anomáliát úgy tudjuk feloldani, ha a két ágat felcseréljünk a tagadott feltétel alkalmazásával. A > logikai operátor ellentettje a <= relációs jel.

4
   while i<=N do

Ezt a ciklus magjának kell követnie, ami esetünkben egy újabb rombusszal (feltétellel) kezdődik. Most azonban azt vehetjük észre, hogy a két ág egy későbbi pontban találkozik és együtt haladnak tovább. Ez egyértelműen elágazást jelent. Először mindig az igaz ágat kell leírnunk pszeudokódban. Észrevehetjük, hogy az egyik ágban egyetlen utasítás sincs, míg a másikban egy értékadás elemi lépés szerepel. Egy elágazásnak pszeudokódban csak az else (azaz hamis) ága hagyható ki, csak az lehet üres. Jelen esetben viszont pont ez az üres ág van ellátva az igaz címkével. Ezt az ellentmondást is kezelni tudjuk a feltétel megfordításával.

5
6
7
     if i%2!=0 then
       s = s+i
     endif

Mivel az egyik ág üres, így tehát nincs else kulcsszó, vagyis a két ág találkozási pontja az endif kulcsszóval adható meg pszeudokódban. Ezt egy inkrementálás követi. A folyamatábrán innen a nyíl mentén visszajutunk a ciklusfeltételhez. Vagyis ennek megfelelően az enddo kulcsszót írjuk le pszeudokódban. Figyeljünk az indentálások helyes használatára is! A folyamatábrán a ciklus feltételét tartalmazó rombuszból kiinduló nem hurkolódó ágat kell ezután leírnunk. Ez egyetlen egyszerű kimenet megadását jelenti.

 8
 9
10
     i = i+1
   enddo
   output s

Kész is vagyunk, megtörtént a fenti folyamatábra pszeudokóddá alakítása. Természetesen itt is léteznek alternatív algoritmusok. Egy teljesen más gondolatmeneten alapuló hatékonyabb megoldás így nézhet ki pszeudokódban.

1
2
3
4
5
6
7
8
9
   input N
   if N%2==0 then
     N = N-1
   endif
   while N>0 do
     s = s+N
     N = N-2
   enddo
   output s

A ciklus magja egyszerűbb és kevesebbszer is kell ismételni, ráadásul a korábbi i változó használatát is megspóroltuk. Persze, ha a számtani sorozatokat jól ismerjük, akkor a matematikai tudásunkat felhasználva még hatékonyabb megoldást is kaphatunk:

1
2
3
4
5
6
   input N
   if N%2!=0 then
     output ((N+1)*(N+1))/4
   else
     output (N*N)/4
   endif

Látszik tehát, hogy amennyiben nem csak a helyes megoldás megtalálása a cél, hanem a hatékonyság is, akkor érdemes jól átgondolni az algoritmusainkat. Aki ezt nem hiszi el, hajtsa végre a mind a 3 algoritmusverziót N=20 bemenet esetén!

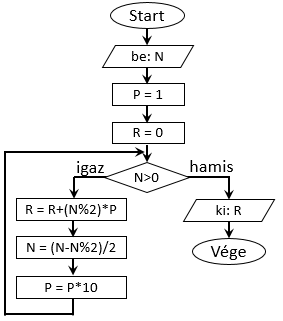
3. példa: Vegyünk elő most egy másik problémát és hozzuk létre az ezt megoldó algoritmust pszeudokóddal! Bontsunk egy pozitív egész számot prím tényezőkre! Másképpen megfogalmazva a feladatot adjuk meg azoknak a csak eggyel és önmagukkal osztható számoknak a sorozatát, amelyeknek a szorzata a bemenetként megadott szám! Először is a felhasználónak meg kell adnia a konkrét számot, aminek értékét az algoritmusunkban az N nevű változóban tároljuk.

1
   input N

A probléma megoldásához ezt a számot osztogatnunk kell más értékekkel figyelve arra, hogy az osztó prímszám-e. Tehát kell egy változó, nevezzük P-nek, melyben az aktuális osztó értékét tároljuk. Ennek kezdeti értéke legyen a legkisebb prím, azaz a 2!

2
   P = 2

Ezt követően minden egyes prím tényezőt ciklikusan megkeresünk, tehát biztosan egy while kulcsszó következik. Azonban mielőtt meghatároznánk a ciklus feltételét, először írjuk le a ciklusmag lépéseit! Mit kell ismételgetnünk a cél elérésének érdekében? Meg kell vizsgálnunk az oszthatóságot és azt, hogy az osztó prím-e. Két szám akkor osztható, ha az osztás során a maradék nulla. Ez tehát egy elágazást eredményez, ami a ciklusmagon belül van, ezért kezdhetjük a sorát egy kicsit bentebb.

4
     if N%P==0 then

Először az igaz esetet kell leírnunk, azaz ha N osztható P-vel. Ebben az esetben tehát P lehet egy N-et eredményező szorzat egyik tényezője. Azonban ez az N osztó lehet, hogy többször is előfordul a tényezők között (gondoljunk a hatványokra). Nekünk mindegyik előfordulásra szükségünk van. Ezeknek a megtalálásához használjunk egy kis trükköt! Ha találtunk egy P osztót, akkor a későbbiekben már ne az eredeti N értéket vizsgájuk, hanem az N/P hányadost, aminek az értékével akár felül is írhatjuk a számunkra többé már nem használandó eredeti N változó értéket. Az alábbi értékadás a cikluson belüli elágazáson belül van, ezért duplán indentáljuk.

5
       N = N/P

Ha erre az új értékre többször is végrehajtjuk a ciklusmag lépéseit, akkor P minden előfordulását megtaláljuk a tényezők között. Viszont bennünket csak prím tényezők érdekelnek. Ahelyett, hogy egy újabb ciklusban megvizsgálnánk, hogy az aktuális P érték mivel is osztható egyáltalán, inkább gondolkozzunk egy kicsit! P értéke kezdetben 2, ami egy prímszám. Később ezt az értéket folyamatosan növelni akarjuk, hogy teszteljünk más számokat is. A 3 is prím. A 4 viszont már nem az. A kérdés az, hogy ez zavarja-e a megoldás menetét. Mivel korábban a 2-t, mint lehetséges osztót megvizsgáltuk és felderítettük az összes előfordulását, biztosak lehetünk benne, hogy az aktuális N érték nem osztható 4-gyel, mert akkor már korábban osztottuk volna kétszer is 2-vel. Másként fogalmazva, mivel a P-nél kisebb értékekkel már osztottunk korábban az aktuális P csak akkor lehet osztó, ha prím. Ebben az esetben viszont ki is kell őt írnunk, mint a keresett prím tényezők egyike.

6
       output P

Nézzük most azt az esetet, amikor az oszthatóság nem teljesül! Ez lesz az elágazás hamis ága, amiben választanunk kell egy új osztójelöltet, ezért vesszük a következő egész számot és eltároljuk P-be!

7
8
9
     else
       P = P+1
     endif

Ezzel a ciklus magját be is fejeztük, a következő sor az enddo kulcsszót tartalmazza (már nem indentálva). Viszont hiányzik még a ciklus feltétele. A megfelelő osztók keresését ciklikusan végezzük, kezdve tehát a P=2 esettel, majd szükség esetén a P értékét növelni kell az osztandó N értékét pedig esetleg csökkenteni. Abban biztosan lehetünk, hogy az ismétlést nem kell folytatnunk, ha a P osztó értéke nagyobb lesz, mint maga az N osztandó. Ebből következik a ciklus feltétele:

3
   while P<=N do

A ciklusból való kilépés egyben azt is jelenti, hogy megtaláltuk és kiírtuk az összes prím tényezőt, azaz az algoritmus befejeződhet. A teljes pszeudokód a fentiek alapján tehát így néz ki:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
   input N
   P = 2
   while P<=N do
     if N%P==0 then
       N = N/P
       output P
     else
       P = P+1
     endif
   enddo

Ha esetleg a módszer nem lenne teljesen ismeretlen, az nem a véletlen műve. Ugyanez az algoritmus szerepel folyamatábrával megadva az előző fejezet végén található feladatsorban.

Az algoritmusok további általános eszközei kizárólag pszeudokóddal lesznek bemutatva. Ezek közül elsőként a tömbökről szerezhet információt az olvasó a következő fejezetben.

4.4. Szójegyzék

indentálás

A kód sorainak bentebb kezdése (behúzása) az őt tartalmazó szerkezeti egységen (ciklusmagja, elágazás ága) belül. Tehát a do-enddo, a then-else, az else-endif és hamis ág nélküli elágazás esetben a then-endif kulcsszópárok közötti sorokat érdemes behúzni.

kulcsszó

Olyan karaktersorozat, melynek konkrét jelentést tulajdonítunk, nem használhatjuk más célra (például változónévként). Ezek a lefoglalt szavak fontos szerepet töltenek be a pszeudokódban.

pszeudokód

Algoritmusok egy olyan szöveges megadási módja, amely formailag nagyon hasonlít egy egyszerűsített valódi számítógépes program szövegére, bár a számítógép közvetlenül nem tudja értelmezni.

4.5. Kérdések, feladatok

  • Mit ad eredményül az alábbi algoritmus, ha bemenetként a=7 és b=3 értékeket kap?

    1
2
3
4
5
6
7
8
       input a
   input b
   c = a
   while b>0 do
     b = b-1
     c = c-1
   enddo
   output c

  • Mire szolgál a fenti algoritmus? Mi az összefüggés a bemenetek és a kimenet között?

  • Mit ad eredményül az alábbi algoritmus, ha bemenetként A=30 és B=105 értékeket kap? Mit csinál az algoritmus? [S403]

    1
2
3
4
5
6
7
8
       input A
   input B
   while B>0 do
     C = B
     B = A%B
     A = C
   enddo
   output C

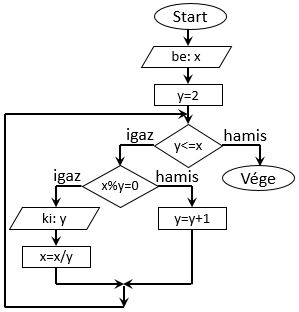
  • Írd le az alábbi folyamatábrával megadott algoritmust pszeudokóddal! [S404]

    Kettes számrendszerbe váltás folyamatábrája

  • Alakítsd át az alábbi folyamatábrával megadott algoritmust pszeudokódá! [S405]

    Példa folyamatábra

  • Írj le egy algoritmust pszeudokód segítségével, amely egy bemenetként megadott egész számról eldönti, hogy páros-e vagy nem! A kimenet a "páros" vagy "páratlan" szavak egyike legyen!

  • Írj le egy algoritmust pszeudokód segítségével, amely az x bemenetet emeli y hatványra! Az x bemenet (alap) tetszőleges valós szám lehet, míg az y (kitevő) egy nem negatív egész számot jelent.

  • Írj le egy algoritmust pszeudokód segítségével, amely három pozitív valós számról eldönti, hogy azok lehetnek-e egy derékszögű háromszög oldalhosszúságai! Használd fel a Pitagorasz-tételt! Ha van ilyen oldalhosszúságokkal rendelkező derékszögű háromszög, akkor valamelyik két oldalnak a négyzetösszege megegyezik a harmadik oldal négyzetével. [S408]

  • Írj egy pszeudokóddal megadott algoritmust, mely két egész számot vár bemenetként! A bemeneteket nevezzük A-nak és B-nek! Az algoritmus határozza meg a két szám közötti (beleértve magukat a bemeneti értékeket is) egész számok összegét!

  • Adj meg pszeudokód segítségével egy algoritmust, amely eldönti egy egész számról, ahogy az prím szám-e! [S410]

  • Írj le egy algoritmust pszeudokód segítségével, amely a bemenetként megadott két pozitív egész szám legkisebb közös többszörösét határozza meg!

  • Alkosd meg azt a pszeudokódot, amely a Fibonacci-sorozat első 20 értékét jeleníti meg kimenetként! [S412]