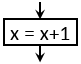3. A folyamatábra

Eddig az algoritmusokat természetes emberi nyelven megfogalmazott, számozott mondatokkal írtuk le. A mondatok egyértelmű és egyszerű tevékenységeket írtak le. Alap esetben a számozás határozta meg végrehajtás sorrendjét. Ebben a fejezetben egy új, széles körben ismert megjelenítési technikával, az úgynevezett folyamatábrával fogunk megismerkedni.

3.1. Alapelemek

A folyamatábra nem más, mint algoritmusok grafikus megjelenítése. Az egyes elemi lépéseket alakzatok segítségével jelenítjük meg, majd ezeket nyilakkal kötjük össze, amelyek meghatározzák az egyes tevékenységek végrehatásának sorrendjét. A különböző jellegű tevékenységekhez különböző alakzatok tartoznak.

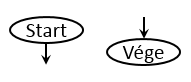
Start- és Vége szimbólum: Ezek az ellipszis alakzatok határozzák meg azt, hogy hol kell elkezdenünk az algoritmus végrehajtását, illetve azt, hogy mikor értük el a lépéssorozat végét. A Start szimbólumból maximum egy lehet egy folyamatábrában. Csak egyetlen kifelé irányuló nyíl indulhat ki belőle és befelé irányuló nyíl nem kapcsolódhat hozzá. A Vége szimbólumból több is szerepelhet egy folyamatábrában, mindig elegendő pontosan egy végjel. Egy vagy több nyíl is mutathat irányába, viszont nem indulhat ki belőle egy sem.

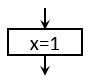
Elemi tevékenység: Egy téglalap alakzatban szereplő egyszerű és egyértelmű lépés, amely nem igényel további magyarázatot. Az alábbi ábrán szereplő tevékenység például egy értékadás, ami azt jelenti, hogy az X nevű mennyiség (más néven változó) értéke legyen innentől kezdve 1. Egy vagy több bemenő nyíl és pontosan egy kimenő nyíl tartozhat hozzá.

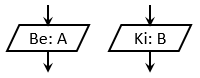
Input- és Output szimbólum: A legtöbb algoritmusnak szüksége van valamiféle bemeneti adatra. Ezt általában a felhasználó a végrehajtás során fogja csak megadni és ezt az értéket fogja az algoritmus felhasználni (hasonlóképpen, mint az általánosítást bemutató példában). A kapott érték mindig eltárolásra kerül az alakzatban megadott nevű mennyiségben. Máskor az algoritmus egy eredményt szolgáltat, közölni szeretne valamit a felhasználóval. A kimenet lehet például egy mennyiség értéke (mint a lenti példában), másrészt lehet egy egyszerű szöveg, mint például a „Szia!” üzenet. A szövegkonstansok mindig macskakörömben szerepelnek, így tudjuk őket megkülönböztetni a mennyiségnevektől. Ezekből a szimbólumokból csak egy nyíl mutathat kifelé.

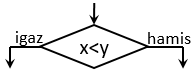
Feltétel szimbólum: A folyamatábrák legösszetettebb szerkezetű és működésű eleme. Egy csúcsára állított rombuszban egy állítás szerepelhet. Az állítás egy logikai kifejezés, amely vagy igaz, vagy hamis kell kegyen. Miután kiértékeltük ezt a feltételt, azaz meghatároztuk az igazságtartalmát két lehetőség közül választhatunk. Ha a feltétel igaz, akkor amentén a nyíl mentén kell folytatnunk a végrehajtást, amely felé az igaz (esetleg az igen) szó van írva. Ha az állításról kiderül, hogy hamis, akkor a hamis (esetleg a nem) címkével ellátott nyíl mentén kell tovább haladnunk. Tehát a rombuszból mindig két felcímkézett nyíl mutat kifelé az oldalán.

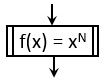
Beágyazás szimbólum: Előfordul, hogy egy folyamatábrában alkalmaznunk kell egy alapvetően több lépésből álló utasítássorozatot. Ha azt már korábban definiáltuk, leírtuk, de most nem szeretnénk ezt újra megtenni, akkor használhatjuk a dupla oldalú téglalap alakzatot a beágyazás szimbólumaként. Ezzel valósíthatjuk meg a korábban tárgyalt egyik algoritmus módosítási módszert. Az alábbi ábrán azt láthatjuk, hogy ki szeretnénk számolni az x mennyiség N. hatványát, ami alapvetően egy számos lépést tartalmazó tevékenység, de itt most csak hivatkozunk erre a korábban valószínűleg már leírt algoritmusra, mint egyfajta új elemi lépésre. A beágyazás szimbólumhoz kapcsolódó nyilakról ugyanazt mondhatjuk el, mint az elemi tevékenység esetén.

Bizonyos elemek esetén tehát előfordulhat, hogy több mint egy befelé mutató nyíl kapcsolódik hozzájuk. Ilyen esetben használhatjuk azt a jelölést, amikor az alakzat felé tartó nyilak egy pontban találkoznak és innen már csak egyetlen nyíl halad tovább az adott alakzat felé. (Később számos példát látunk majd rá.)

3.2. Az algoritmus alapszerkezetei folyamatábra esetén

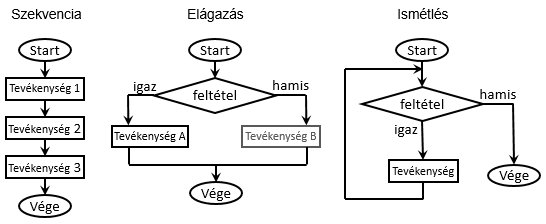
Természetesen az algoritmusok három alapszerkezete folyamatábra segítségével is leírható. A szekvencia itt nyilakkal összefűzött tevékenységeket jelent. A nyilak egyértelműen meghatározzák a végrehajtás sorrendjét, mert összefűzésükkel csak egyetlen útvonal jön létre. Egy alakzatból csak akkor mehetünk tovább a nyíl mentén, ha az adott tevékenységet maradéktalanul végrehajtottuk. A tevékenységeket nem szükségszerű fentről lefelé vagy balról jobbra elhelyezni, mivel úgyis a nyilak határozzák meg az egymáshoz való viszonyukat.

Az elágazás egy feltétel segítségével valósítható meg. A rombuszt elhagyó nyilak egy-egy tevékenységre vagy tevékenységcsoportra mutatnak. Viszont ezek felírása után a két ágnak egyesülnie kell, azaz két nyíl egy pontban találkozik és egybeolvadva halad tovább. Az értelmezés a következő. Amikor elérkezel egy feltételhez, ki kell értékelni a rombuszban lévő logikai kifejezést. Ha ez a feltétel teljesül, haladj tovább az igaz ágon és hajtsd végre az ott található utasításokat és miután elérted a nyilak találkozási pontját, folytasd az elágazás utáni következő tevékenységgel! Ellenben ha a feltétel nem teljesül folytasd a hamis ág mentén a végrehajtást, majd végül ebben az esetben is az elágazás utáni utasításra kerül a sor. Tehát a két ág közül pontosan az egyik hajtódik végre (a feltételtől függően). Bármelyik ágról is legyen szó, minden esetben a végrehajtás ugyanúgy folytatódik. Néha a kétirányú elágazás egy speciális esete válik szükségessé, amikor az egyik ág egyetlen tevékenységet sem tartalmaz. Ez tehát azt jelenti, hogy vagy végrehajtunk egy lépést vagy kihagyjuk azt. A későbbiekre való tekintettel célszerű, ha a kihagyható tevékenység az igaz ágban helyezkedik el és így a hamis ág üres lesz (egyetlen nyíl a találkozási ponthoz).

Az ismétlések is feltétel segítségével írhatóak le. A feltételt tartalmazó rombuszból kiinduló egyik tevékenységsorozat ebben az esetben olyan, hogy előbb-utóbb a sorrendet jelentő nyilak mentén visszajutunk a már korábban is érintett feltételhez. Tehát egy hurok alakul ki. A feltétel másik oldalán ilyet nem találunk. A végrehajtás szempontjából tehát először kiértékelődik a feltétel. Ettől függően vagy belépünk a ciklusba, végrehajtjuk az ott található utasításokat, majd újra kiértékeljük a feltételt vagy egyszerűen a másik irányban haladunk tovább. Egyelőre magyarázat nélkül fogadjuk el, hogy a ciklusmag, vagyis az ismétlendő utasítások mindig a feltétel igaz oldalán helyezkednek el. Röviden tehát azt mondhatjuk, hogy az ismétlés addig történik, amíg a feltétel igaz és amint hamisnak bizonyul tovább lépünk. Fontos megjegyezni, hogy az ismétlendő utasítások hatással kell, legyenek a feltételre, ha ugyanis ez nem teljesül, akkor a feltétel mindig igaz marad, azaz sohasem lépünk ki a ciklusból. Egy algoritmusnak azonban végesnek kell lennie.

A fenti ábrán a három alapstruktúra van szemléltetve folyamatábra segítségével. Az elágazás esetén a Tevékenység B azért van szürke színnel feltüntetve, mert a megbeszéltek szerint ez az ág lehet üres, azaz a tevékenység kihagyható. Mint látható az elágazás és az ismétlés is tartalmaz feltételt. Azonban könnyű őket elkülöníteni, ha figyelembe vesszük, hogy elágazás esetén a végrehajtás két ága később mindig összetalálkozik, míg ismétlés esetén ez nem történik meg, de az egyik ágon mindig visszajutunk az feltétel elé.

3.3. Egy hétköznapi példa

Adjuk meg azt a lépéssorozatot, amely egy nyilvános, érmés telefonkészülék használatát mutatja be. Tételezzük fel, hogy a fülkében vagyunk, ismerjük a felhívandó telefonszámot és vannak megfelelő érméink. Első körben azt gondolhatjuk, hogy a feladat egyszerű:

1. Vedd fel a kagylót!

2. Dobd be az érmét!

3. Tárcsázd a számot!

4. Beszélj!

5. Tedd le a kagylót!

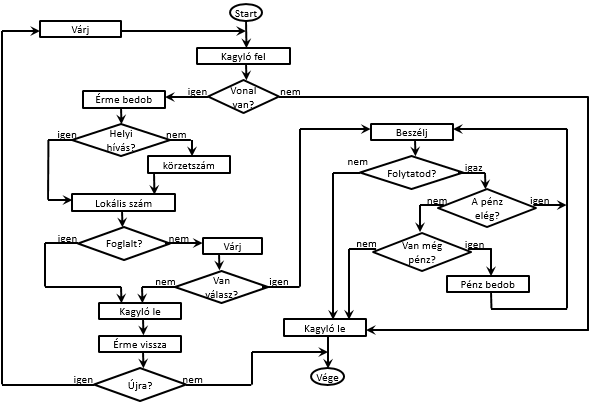
Azonban, ha alaposabban átgondoljuk a feladatot, rájövünk, hogy vannak kezeletlen eshetőségek. Módosításra van tehát szükségünk. Mi a teendő, ha a készülék nem működik? Mi a teendő, ha a vonal foglalt? Mi a helyzet, ha a hívott fél nem veszi fel? Mi történik akkor, ha lebeszélted az összes érméd? Az ilyen és hasonló szituációk kezeléséhez ki kell terjesztenünk az algoritmust. Hamar rájövünk, hogy újabb lépések kellenek és nem mindegyik szükséges minden esetben. A teljes algoritmus leírása mondatszerű formában egy elég hosszú és átláthatatlan utasítássorozathoz vezetne. A folyamatábra alkalmazásával ez a javított komplex algoritmus kissé átláthatóbb és könnyebben követhető formában adható meg. Íme, a megoldás:

Látható, hogy a kagyló felvétele után meg kell vizsgálnunk, hogy van-e vonal (működik-e a készülék). Ha nem, akkor csak letesszük a kagylót és a folyamat már véget is ért. Ha van vonal, bedobjuk az érmét, majd előhívószám alkalmazásával vagy a nélkül tárcsázzuk a számot. Amennyiben foglalt jelzést kapunk letesszük a kagylót és visszavesszük az érmét. Folytatásként egy döntést kell hoznunk: Mivel a partner telefonközelben van próbáljuk-e meg a hívást ismét egy kis idő után? Ha úgy döntünk, hogy nem éri meg a várakozás, akkor a folyamat ismét véget ér, távozhatunk. Azonban ha az újrahívás mellett döntünk, akkor rövid várakozás után elölről kell kezdenünk a teljes folyamatot. Kezelnünk kell továbbá azt a helyzetet, amikor a telefon kicseng (nem foglalt). Ha egy ideig nincs válasz, akkor ez lesz a harmadik eset, amikor le kell tennünk a kagylót és a második, hogy vissza kell vennünk az érmét. Ellenben, ha van válasz, akkor kezdjük el a beszélgetést. A folyamatábráról leolvashatjuk, hogy le kell tennünk a kagylót ha már nem akarunk beszélni, illetve akkor is, ha már lebeszéltük a bedobott összeget és már nincs több érménk. Minden más esetben folytathatjuk a beszélgetést.

3.4. Változók

Az előző példa egy egyszerű hétköznapi élethelyzetet ír le. Mivel az olvasó bizonyára előbb-utóbb jó programozó szeretne lenni, a továbbiakban olyan problémák kerülnek tárgyalásra, amelyek egyszerű számítógéppel is megoldhatóak. Ezek többnyire egzaktabb, a matematika segítségével kezelhető problémák lesznek. Ilyenkor gyakran kell bizonyos mennyiségek értékét tárolnunk, ezekkel az értékekkel műveleteket végeznünk, belőlük új értékeket meghatároznunk. Ennek a munkának a megkönnyítésére bevezetjük a változó fogalmát. A változó egy mennyiség értékének tárolására szolgáló névvel rendelkező objektum. Ezzel a névvel tudunk hivatkozni az eltárolt értékre. A név általában (bizonyos korlátokat figyelembe véve) szinte tetszőleges lehet. Gyakorlati szempontból az a praktikus, ha a név utal a tárolt mennyiség mivoltára. Ha például azt akarjuk nyilvántartani, hogy egy tárgy milyen nehéz, akkor bevezethetünk egy például tömeg nevű változót és azt mondhatjuk, hogy ennek az értéke legyen 16. Egy utóbbit egy értékadás nevű művelet segítségével adhatjuk meg tömeg=16 formában. Ez egy elemi művelet. Az egyelőség jel bal oldalán mindig egy változó neve kell, álljon, míg a jobb oldalon egy értéket kell meghatároznunk. Az 23=hossz tehát formailag helytelen értékadás. Tartsuk továbbá azt is szem előtt, ez nem egy egyenlőség vizsgálat, tehát nem azt jelenti, hogy a 23 vajon egyenlő-e a hossz változó értékével. (Míg az egyelőség vizsgálat két oldala felcserélhető, addig az értékadásé nem.)

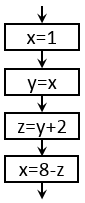
Az értékadás jobb oldalán nem csak egy konstans érték szerepelhet. Megadhatunk itt másik változót vagy akár egy matematikai kifejezést is amelyet először ki kell értékelni és az így kapott értéket kell eltárolni a bal oldalon megadott változóban. Nézzünk egy folyamatábra részletet ennek szemléltetésére:

Az először végrehajtandó lépésben az x nevű változóban eltároljuk a 1 értéket. A második azt jelenti, hogy y értéke legyen ugyanannyi, mint az x értéke, tehát 1. A harmadik elemi lépés szerint a z jelentse az y aktuális értékénél kettővel nagyobb szám, azaz z értéke 3 lesz. A negyedik utasítás jobb oldalán szereplő kifejezés értéke 5, mivel az előző lépés értelmében a z értéke 3 jelenleg. Ezt az 5-ös értéket kell eltárolnunk az x változóba, felülírva az eddig ott tárolt értéket. Mint neve is mutatja egy változó értéke megváltozhat. Ha ugyanaz a név többször is szerepel értékadás bal oldalán, akkor az algoritmus egy adott pontján a változó aktuális értékét mindig a legutóbbi értékadás határozza meg.

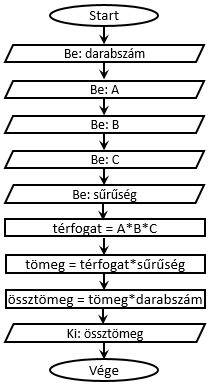
Nézzünk egy életszerűbb példát! Mennyi a tömege 8 darab olyan arany tömbnek, amelyek mindegyike téglatest alakú és ennek a téglatestnek az oldalhosszúságai rendre 5cm, 10cm és 20 cm? (Az arany sűrűsége 19,2g köbcentiméterenként.) Ez egy nagyon konkrét probléma. A megoldáshoz szükséges minden adat ismert az algoritmus létrehozásának pillanatában. Érdemes azonban megfontolni, hogy vajon később más adatokat tartalmazó, de hasonló problémák megoldására is szükség lesz-e. Általában igen, ezért érdemes máris egy általánosított algoritmust létrehozni tetszőleges méretű, anyagú és darabszámú tömbök kezelésére. Ez azt jelenti, hogy amikor a folyamatábrát létrehozzuk, még nem ismerjük az adatokat és a mennyiségek (változók) segítségével általánosan kell leírnunk a probléma megoldásának menetét. A konkrét értékek majd csak később, a végrehajtás során derülnek ki, az algoritmus felhasználója fogja csak megadni őket és ezeket változókba (darabszám, A, B, C, sűrűség) mentjük. Az első lépések tehát a konkrét értékek bekérése, input szimbólumok segítségével. Ezeket az értékeket megfelelő változókban tároljuk. Ezután meg kell határoznunk egy tömb térfogatát az oldalhosszúságok alapján és az eredményt egy külön változóba mentjük. A következő lépésben pedig kiszámítjuk és eltároljuk egy tömb tömegét, végül meghatározzuk az tömbök össztömegét. Ezt ugyan eltároljuk egy újabb változóba, de még meg is kell osztanunk ezt az információt a felhasználóval egy output utasítás révén. A problémát megoldó algoritmus folyamatábrája a fentiek alapján tehát a következő paralelogrammákat és téglalapokat is tartalmazó szekvenciával írható le:

3.5. Inkrementálás és dekrementálás

Az értékadás egy speciális esete az, amikor a változó új értéke függ a régitől. Például ha az x változó értékét meg szeretnénk növelni eggyel, akkor a következőt kell írnunk.

Első ránézésre furcsa lehet ez a leírás annak, aki a matematika oldaláról közelíti meg. Nincs olyan véges érték, amely kielégítené az egyenletet. Azonban ez nem matematika, hanem programozás illetve nem egyenlet, hanem értékadás. Az értelmezés és a végrehajtás az egyenlőségjel jobb oldalán kezdődik. Meghatározzuk az x+1 kifejezés értékét, majd ezt a számot eltároljuk az egyenlőségjel bal oldalán megadott változóba. Ha eddig az x értéke 5 volt, akkor ezután már 6 lesz. Ezt inkrementálás-nak nevezzük.

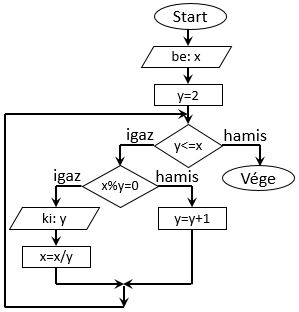
Nézzünk egy példát, ahol ezt felhasználjuk. Egy tipikus probléma, amit számítógéppel könnyű megoldani, egy pozitív egész szám faktoriálisának meghatározás. Mennyi 5! értéke? Hogy kell ezt kiszámolni? Matematikából azt tanultuk, hogy egy szám faktoriálisa nem más, mint 1-től az adott számig az összes egész szám szorzata. Írjuk le ezt egy folyamatábrával! Az algoritmus elején be kell kérnünk egy értéket a felhasználótól. Ez a bemeneti érték lesz az a pozitív egész szám, aminek a faktoriálisát meg szeretnénk határozni. Egy paralelogrammába elhelyezett bemeneti utasításban az megadott értéket a szám nevű változóba tároljuk el. Abban is biztosak lehetünk, hogy szükség lesz egy ciklusra, ugyanis többször meg kell ismételnünk legalább a definícióban szereplő szorzás műveletét. Ahhoz, hogy tudjuk hányadik ismétlésnél járunk, be kell vezetnünk egy segédváltozót, ami tehát azt tárolja, hányadik iterációnál tartunk. Természetesen értéke kezdetben 0. Mit kell a ciklus magjában tennünk? Mit kell ismételgetnünk? Egyrészt növelnünk kell a segéd változó értékét eggyel, azaz inkrementálnunk kell egy téglalapban. Ha így teszünk, rájöhetünk, hogy inkrementálás után a segéd értéke éppen a következő pozitív egész szám, ami a faktoriális kiszámolásához szorzótényezőként szükséges. Másrészt végre kell hajtanunk magát a szorzást. Össze kell szorozni az eddigi részeredményt a segéd változóban aktuálisan tárolt természetes számmal. A szorzat lesz az új részeredmény. Míg a hétköznapokban a számolás során a részeredményeket akár fejben is tarthatjuk, addig az algoritmusok esetén minden értéket el kell tárolni valahol. Bevezetünk tehát egy újabb változót a részeredmény (majd végül a végeredmény) tárolására. Ezt fakt-nak nevezem a példában. A fentiek értelmében tehát a ciklusmagban lennie kell egy fakt = fakt*segéd utasításnak is. Vegyük észre, hogy az ilyen jellegű utasításoknak (amikor egy változó az értékadás mindkét oldalán szerepel) van egy speciális tulajdonsága/igénye! Az utasítás előtt a fakt változónak már rendelkeznie kell értékkel, különben nem tudjuk megmondani milyen értéket kell megszorozni a segéd értékével. Kell tehát adnunk egy kezdő értéket a fakt-nak a ciklus előtt. Mivel a változó egy szorzó tényező, a természetes számok halmazának multiplikatív egységeleme, azaz az 1 tökéletes választás. Ráadásul az 1!=1 definíció is ezt a választást sugallja. A ciklusmag végrehajtása után vissza kell térnünk a ciklus feltételhez, amit egy csúcsára állított rombuszba írunk. Meddig kell folytatni az ismételgetést? Amíg a segéd, azaz a legutóbbi szorzótényező kisebb, mint a megadott szám. Amint a segéd értéke egyenlővé válik a szám értékével kiléphetünk a ciklusból és folytathatjuk a végrehajtást a feltétel hamis ágával. Egyetlen dolgunk maradt. A kapott eredményt, ami most a fakt változóban van, meg kell osztanunk a felhasználóval egy kimeneti utasítás révén. A végeredmény így néz ki.

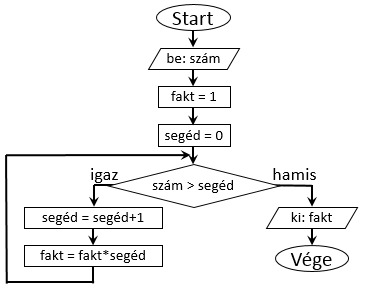
Úgy gondoljuk, készen vagyunk, de ahogy mondani szokás: puding próbája az evés. Ellenőrzésképpen alkalmazzuk a kapott folyamatábrát néhány konkrét esetben! Számoljuk ki mondjuk, hogy mennyi 5! és közben kövessük, hogyan változnak a változóink értékei! A Start szimbólumtól indulva először elmentjük a bemenetként megadott értéket (jelen esetben az 5-öt) a szám változóba. Ezután két változó kezdőértékadása következik. A fakt értéke most 1 lesz, majd a segéd változóé pedig 0. (Eddig nem volt ismert az értékük.) Elérkezünk a feltételhez. El kell döntenünk, hogy a rombuszban megadott állítás igaz-e. Mivel szám=5 és segéd=0, így a 5>0 feltétel igaznak bizonyul, ezért a baloldalon haladunk tovább. Inkrementáljuk a segéd értékét, majd megváltoztatjuk a fakt változó tartalmát. Mivel ekkor fakt=1 és segéd=1, a szorzatuk (1) felülírja a fakt korábbi értékét. Feleslegesnek tűnhet az 1-et felülírni 1-gyel, de az szerepel most az algoritmusban és nekünk ezt a lépéssorozatot kell követnünk. Ezek után a nyíl visszavezet bennünket a feltételhez, ismét ki kell azt értékelnünk. Az aktuális szám>segéd felírás a 5>1 állítást jelenti, ami ismét igaz feltételt jelent. Újra végre kell hajtanunk az igaz ág két téglalapjában lévő utasítást. A segéd értéke növekszik eggyel, azaz kettő lesz. A fakt pedig ennek megfelelően a duplájára nő. Újra meg kell néznünk a feltételt. Mivel az 5>2 állítás igaz, továbbra is ismételnünk kell. A segéd értéke tovább nő, a fakt pedig felveszi a 2*3 szorzat értékét. A feltétel továbbra is igaz, azaz megint belépünk a ciklusmagba, ahol segéd értéke 4, a fakt-é 24 lesz. Mivel a feltétel továbbra is igaz, az ismétlés folytatódik. Az inkrementálás hatására a 4+1 érték, vagyis az 5 tárolódik el a számlálásra használt változóba, a fakt új értéke pedig a 24*5 kifejezés miatt 120 lesz. Ezután a nyilak mentén újra a feltételhez jutunk. A szám>segéd formális kifejezésbe behelyettesítve a változók aktuális értékeit 5>5 feltételt kapunk. Ez nem egy igaz állítás, tehát a rombusz jobb oldalán lévő, hamis címkével ellátott nyilat kell követnünk. Egy kimeneti utasításhoz jutunk, melynek értelmében közölnünk kell a felhasználóval a fakt változó aktuális értékét. És valóban 5! nem más, mint 120. Az algoritmus véget ért és jól működött. A felhasznált mennyiségeink lépésről-lépésre történő változását egy táblázatban is követhetjük.

szám	segéd	fakt
?	?	?
5	?	?
5	?	1
5	0	1
5	1	1
5	1	1
5	2	1
5	2	2
5	3	2
5	3	6
5	4	6
5	4	24
5	5	24
5	5	120

Az imént a végrehajtás során észrevettük, hogy nem minden lépés feltétlenül szükséges. Ilyenkor javíthatunk az algoritmus hatékonyságán. Esetünkben, ha azt mondjuk, hogy a ciklusmag első lefutása, vagyis az 1-gyel való szorzás kihagyható, mivel nincs igazi hatása. Ezt elérhetjük azzal, hogy a segéd változónk kezdőértékét (a ciklus előtt) azonnal 1-re állítjuk. Minden változás esetén át kell gondolnunk, hogy a lépéssorozatunk továbbra is helyes-e. Ha már az első cikluslépésben 2-vel szorzunk, hogyan kapjuk meg az 1! értékét? Hajtsuk végre a módosított folyamatábra lépéseit ebben az esetben. A bement adott (1), a fakt is és a segéd is kezdetben 1. A feltétel, konkrétan az 1>1 állítás már egyből hamisnak bizonyul (anélkül, hogy egyszer is végrehajtottuk volna a ciklusmagot), így a kimenet a fakt kezdeti értéke, azaz 1 lesz. Megállapíthatjuk tehát, hogy az algoritmus továbbra is helyesen működik és ráadásul kevesebb lépés végrehajtásával ad eredményt, mint a fenti ábrán megadott eredeti verzió.

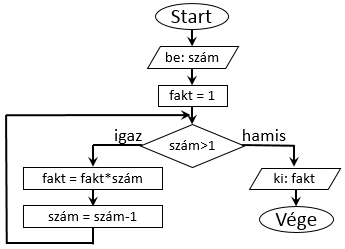
Gyakorlásképpen nézzük meg egy másik megoldását ugyanennek a problémának! Ez tehát egy alternatív algoritmust megvalósító folyamatábra, amely szintén leírja, hogyan kell egy pozitív egész szám faktoriálisát meghatározni.

Itt egy trükköt használtunk fel. Mivel a szorzás felcserélhető, kezdhetjük a részeredmények kiszámítását a legnagyobb egész számmal, azaz az eredeti bementi értékkel, majd egyre kisebb számokkal folytathatjuk. Mivel így a szám változó eredeti értékre már nem lesz szükség az továbbiakban, felhasználhatjuk azt a változót arra, hogy ebben tartjuk nyilván az aktuális szorzótényezőt. Tehát minden cikluslépésben eggyel csökkenthetjük az értékét azaz dekrementáljuk, majd felhasználhatjuk a további szorzásokban. A változó értékét mindaddig csökkenthetjük, amíg nagyobb, mint 1 (hatékonysági okok miatt). Így viszont a segéd nevű változóra nem is lesz szükségünk, elhagyhatjuk. (Később memóriahasználat szempontjából hatékonyabb program alapjául szolgálhat.) Ez a megoldás is mindig ugyanazt az eredményt adja, mint a korábbi. Ezt a következő táblázat segítségével is ellenőrizhetjük, melyben a változók értékeit követjük nyomon abban az esetben, amikor a bemenet 5.

szám	fakt
?	?
5	?
5	1
5	5
4	5
4	20
3	20
3	60
2	60
2	120
1	120

Az a műveletet, mely során egy változó értéke eggyel csökken az a dekrementáció. Például: y = y-1.

3.6. Operátorok

Az egyes értékekkel (például konstansokkal, változókkal) különböző műveleteket hajthatunk végre. Láttunk már példát összeadásra, kivonásra és szorzásra. Az alapvető aritmetikai műveleteken kívül számos más műveletet is eltudunk végezni. Egyes programnyelvek esetén akár félszáz különböző műveletről is beszélhetünk. Ezeket a műveleteket operátor-okkal jelöljük, az értékeket, amelyeken a műveletet végrehajtjuk pedig operandus-oknak nevezzük. Egyes operátoroknak egy, másoknak kettő (esetleg több) operandusa is lehet. Egyes esetekben az operandusszám ismerete is szükséges ahhoz, hogy tudjuk egy operátor milyen műveletet is takar. Szemléltessük ezt egy példával! Az x = -34 értékadás során a - operátor egy operandussal rendelkezik (ez a 34). Ebben az esetben az operátor az érték mínusz egyszeresének meghatározására szolgál (előjelváltás). Ezzel szemben az y = 9-5 értékadásban szereplő - operátornak két operandusa is van, a művelet során pedig ezek különbségét határozzuk meg (kivonás).

Az operátorok és operandusok valamint esetleges kerek zárójelek kombinációjával ún. kifejezéseket hozhatunk létre. A kifejezés-kiértékelés során egyértelműen meg kell tudnunk határozni minden kifejezés értékét. Egyszerűbb esetekben ez nem jelent gondot. Mindenki sejti, hogy a 3+4+5 kifejezés értéke 12. Mi a helyzet azonban a 3+4*5 kifejezéssel. Ez jelenthetne 35-öt vagy 23-at is. Matematikai tanulmányaink alapján tudjuk, hogy a szorzás (* operátor) erősebb, mint az összeadás (+ operátor), azaz hamarabb kell végrehajtani a kifejezés kiértékelése során. Ha a 35 értéket szeretnénk megkapni, akkor külön jeleznünk kell, hogy először az összeadás művelet kerüljön végrehajtásra. Ezt a zárójelekkel tehetjük meg, ilyen formában: (3+4)*5. A kifejezések megadásának az a módja, amit a hétköznapokban használunk, amikor is a kétoperandusú operátor az operandusai között helyezkedik el (ún. infix alak), nem teljesen egyértelmű. Vagy teljes zárójelezést kell használnunk mindig, vagy be kell vezetnünk minden egyes operátorhoz egy erősséget (precedencia) és ez alapján tudnunk kell sorba rendezni az operátorokat. Ez 40-50 operátor esetén már nem is olyan egyszerű dolog. A későbbiekben meg fogunk nézni olyan kifejezések megaadására szolgáló formákat is, ahol precedencia és zárójelek megadása nélkül is egyértelmű a kiértékelés (csak ez sajnos eltér a hétköznapi életben megszokott felírástól).

Már korábban is megfigyelhettük, hogy az értékadás jobb oldalán kifejezés is lehet. Nézzünk egy olyan problémát, ahol több különböző operátort tartalmazó összetettebb kifejezésekre is szükségünk van! Szeretnénk egy tízes számrendszerben megadott (decimális) nem negatív, egész számot kettes számrendszerbe (bináris formába) átváltani. Vagyis a bemenetünk egy olyan adat, amely 10 különböző számjegyet (0-9) tartalmazhat, míg a kimenetben kizárólag a 0 és az 1 számjegyek szerepelnek úgy, hogy a szám értéke ugyanaz maradjon. (Ezzel a kérdéskörrel a 8. fejezetben bővebben fogunk foglalkozni.) Először bemutatom a papíron-tollal történő hagyományos manuális módszert mondatszerű leírással:

1. Írd fel az átváltani kívánt decimális számot és húzz a jobb oldalánál lefelé egy hosszú vonalat!

2. Oszd el a vonal bal oldalán lévő számot kettővel és a hányados egész részét írd az előbbi szám alá a vonal bal oldalára!

3. Az osztás maradékát írd le a kapott egész hányados mellé a vonal jobb oldalára!

4. Amennyiben a legutóbbi osztás során kapott hányados egész része nem 0, akkor folytasd a 2. lépéssel!

5. Különben a vonal jobb oldalán elhelyezkedő számjegyeket (0 vagy 1) alulról felfelé írd egymás mellé! Ez a kívánt bináris szám.

Az eredmény így néz ki a 237 esetén (néhány segédszámítást is feltüntetve):

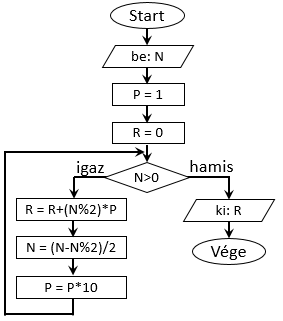
Készítsünk el egy más elven alapuló, alternatív algoritmust erre a problémára folyamatábra segítségével! Természetesen itt is alkalmazunk ismétlést. A ciklus magjában pedig mindig meghatározunk egy új részeredményt úgy, hogy az aktuálisan kapott (bináris) számjegyet egy eddigi részeredmény legnagyobb helyiértékű számjegye elé helyezzük. Emellett szintén a ciklusmagban tartjuk nyilván a bemenetből származó és a következő cikluslépésben felhasználandó decimális értéket is. Első lépés tehát egy bementként megadott szám elmentése (mondjuk az N változóba). Használni fogunk két segédváltozót is. Az R fogja tárolni az aktuális részeredményt. Emellett a P változó fog utalni arra a helyiértékre, ahol a következő bináris számjegyet el kell helyeznünk. Például a P=1000 érték azt jelenti, hogy a (jobbról) negyedik helyiértékre (az ezresekre) gondolunk. Kezdetben tehát P=1 kell, legyen. Ezután következik a ciklus, amit addig kell ismételnünk, amíg az N értéke nagyobb, mint nulla, tehát ez a feltétel kerül a csúcsára állított rombuszba. Ha a feltétel igaz, belépünk a ciklusmagba. Itt ez első elemei lépés egy téglalapban elhelyezett értékadás lesz, amivel a következő kettes számrendszerbeli számjegyet ez eddig már meghatározottak elé helyezzük. Ehhez egy összetett kifejezést használunk. Nézzük ennek részeit! A % operátor (műveleti jel) a maradékos osztás jelölésére szolgáló kétoperandusú operátor. Az A%B megadja azt az egész számot, amelyet hozzá kell adni az A/B hányados egész részének B-szereséhez, hogy visszakapjuk A értékét. Például a 45%13 értéke 6, mivel 45/13=3,461538..., aminek egész része 3. Mivel a 45 és a 3*13 különbsége 6, így ez az egész osztás maradéka (45=3*13+6). Ezáltal az R részeredmény új értékének meghatározása nem más, mint a korábbi érték növelése az új bináris számjegynek (maradékos osztás eredményének) és a P értéknek a szorzatával (R=R+(N%2)*P). A következő lépésben az N értékét csökkentjük azáltal, hogy elvégezzük a kettővel való egészosztást. Ha nem akarunk külön operátort bevezetni az osztásra és az egészosztásra, akkor egy kis trükköt tudunk alkalmazni. Az N érték kettővel történő egész osztásának eredménye felírható (N-N%2)/2 alakban. Hogyan is hajtandó végre az (N-N%2)/2 kifejezés kiértékelése? A zárójel azt jelenti, hogy az abban lévő részkifejezést kell kiértékelni először függetlenül a műveletek erősségétől. A zárójelben viszont még mindig két operátor is szerepel. Előbb egy kivonás, aztán egy maradékképzés. Mivel utóbbi erőssége nagyobb, ezért az N/2 maradékát kell kivonnunk N értékéből. Végül pedig ennek felét kell meghatároznunk, ami biztosan egész szám lesz (N=(N-N%2)/2). A ciklusmag utolsó lépéseként a új pozíciót kell meghatároznunk, ami egy helyiértékkel balra tolást (10-zel szorzást) jelent (P=P*10). A végrehajtás a ciklusfeltétel újbóli kiértékelésével folytatódik. Ha a feltétel hamis kilépünk a ciklusból és végül kiírjuk a végeredménnyé vált R értéket. A számos operátort alkalmazó teljes folyamatábra így néz ki:

3.7. Logikai kifejezések

Egyes kifejezések értéke nem egy szám, hanem egy ún. logikai érték. Két logikai értéket különítünk el, az egyik az igaz a másik a hamis. Mondjuk a 123<321 kifejezés értéke mindig igaz, mert az első operandusként megadott konstans kisebb értéket képvisel, mint a második operandust jelentő literál. A < (kisebb, mint) operátor egy összehasonlító műveletet takar, melynek eredménye az egyik logikai érték. Vannak további, logikai értéket meghatározó összehasonlító operátorok, melyeket az alábbi táblázat foglal össze.

Egy összehasonlító operátor akkor ad igaz értéket, ha az ellentét operátora hamis értéket ad. Ezeknek az ismerete később még hasznos lesz.

A matematikai logika lehetővé teszi, hogy olyan műveleteket is használjunk, amelyeknek nemcsak az értéke, hanem az operandusai is logikai értékűek. Ezekkel az ún. logikai operátorokkal összetettebb feltételeket is megfogalmazhatunk. Egy kétoperandusú logikai operátor esetén az operandusoknak négyféle lehetséges kombinációja van. Ezeket egy igazságtáblákban adhatjuk meg, amelyek a következőképpen néznek ki:

Tehát az ÉS operátor csak akkor ad igaz értéket, ha mindkét operandusa igaz. A VAGY művelet eredménye csak akkor igaz, ha legalább az egyik operandusa igaz. Az XOR vagyis KIZÁRÓ VAGY operátor értéke csak akkor igaz, ha kizárólag csak az egyik operandusa igaz. Van egy negyedik gyakran használt logikai művelet is, amelyet a NEM operátorral adhatunk meg. Ez az egyetlen (logikai értékű) operandusát tagadja, azaz az ellentétes logikai értéket eredményezi. Ezeknek a logikai operátoroknak az értelmezése tehát kissé eltérhet a hétköznapi értelemben vett jelentéstől. Szemléltessük ezt egy példával: Hány ember született Magyarországon 2000-ben ÉS 2001-ben? A matematikai logika szabályai szerint ez azt jelenti, hogy azokra vagyunk kíváncsiak, akik mindkét évben megszülettek. Mivel ez biológiailag egy üres halmaz, az eredmény: nulla. A hétköznapokban a fenti kérdést inkább úgy szokás érteni, hogy mennyi az összege az egyik évben valamint, külön a másik évben született emberek számának. Belátható hogy logikailag sokkal helyénvalóbb lett volna a kérdésben egy VAGY kötőszót használni.

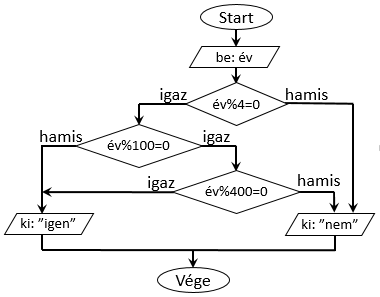
Gyakorlásként oldjuk meg a klasszikus szökőév problémát, először egymásba ágyazott elágazás alkalmazásával. El szeretnénk tehát dönteni egy évszámról, hogy az szökőévre utal-e vagy nem. Eközben legyünk pontosak és használjuk a Gergely naptárbeli definíciót a hétköznapi „minden negyedik év” helyett. A pontos szabály, amelyet alkalmazni szeretnénk így hangzik: Minden 400. év szökőév, továbbá minden olyan 4. év is, amely év nem osztható 100-zal. Értelmezzük az alábbi megoldást jelentő folyamatábrát!

Az adatbekésés után az első feltétel azt írja le, hogy a bemenetként megadott évszámot, ha osztjuk 4-gyel, akkor a maradék nulla-e? Más szavakkal: osztható-e az év 4-gyel? Ha nem, akkor biztosak lehetünk abban, hogy ez nem szökőév, különben viszont újabb feltétel szükséges, mivel nem minden negyedik év szökőév. Ha a 100-zal való osztás maradéka nem nulla, az azt jelenti, hogy nem kerek százasról van szó. Viszont ez a második feltétel az első igaz ágában van, így a 100-zal oszthatóságot csak 4-gyel osztható évekre vonatkozóan kell ellenőriznünk. Ezek után, ha 4-gyel és 100-zal is osztható a szám, akkor (és csak akkor) tudnunk kell, hogy 400-zal is osztható-e. Ha mondjuk a vizsgált évszám a 2019, akkor egy feltétel kiértékelés után biztosan tudjuk a választ, míg év=2000 esetén mind a három feltételt ki kell értékelni. Tehát olyan elágazásokat használtuk, amelyek maguk is elágazást tartalmaznak.

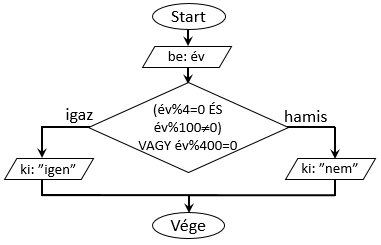
Az iménti bonyolult folyamatábrát leegyszerűsíthetjük, ha egymásba ágyazott elágazások helyett egyetlen (összetett) feltételt fogalmazunk meg. Az eddig használt három egyszerű feltételt kössük össze logikai operátorokkal! Kétféleképpen kaphatunk szökőévet. Az egyik esetben 400 többszöröseiről van szó, míg a másik esetben egyszerre kell teljesüljön a 4-gyel való oszthatóság valamit a 100-zal való oszthatatlanság. Az egyszerre szükséges teljesülést egy ÉS kapcsolattal írhatjuk le. Ezzel szemben, ha elég az egyik feltétel teljesülése is, akkor a VAGY operátort használjuk. Esetünkben ennek a VAGY operátornak ez egyik operandusa ráadásul egy ÉS művelet eredménye, ezért is van szükség zárójelezésre. A teljes folyamatábra így sokkal átláthatóbb (bár cserébe egy összetett feltétellel kell dolgoznunk).

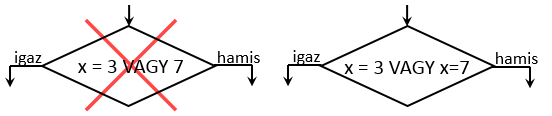
Tapasztalatok alapján érdemes felhívni a figyelmet egy a kezdők által időnként elkövetett alapvető hibára. Egy feltételes utasításban le szeretnénk írni azt logikai kifejezést, amely a hétköznapi szóhasználat szerint szavakba öntve így hangzik: ha az x változó értéke 3 vagy 7, akkor … Az alábbi két folyamatábra-részlet közül az egyik helyes, a másik helytelen.

A bal oldali ábrával az a gond, hogy a VAGY logikai operátor két oldalán logikai kifejezésnek, azaz igaz vagy hamis értéknek kell szerepelnie. Ebben az esetben viszont az operátor jobb oldalán egy szám jellegű érték szerepel, nem logikai. A jobb oldali helyes megfogalmazás szerint vagy az x=3 összehasonlításnak vagy az x=7 összehasonlításnak kellene igaz-nak lennie. Ez az alak azt is kihangsúlyozza, hogy itt két külön összehasonlítást kell elvégeznünk.

3.8. Szójegyzék

ciklusmag

Az ciklusban megismétlendő utasítások sorozata.

dekrementálás

Egy változó értékének eggyel való csökkentése.

értékadás

Egy elemi lépés, mely során (új) értéket rendelünk egy változóhoz. Megváltoztathatjuk vele egy változó értékét.

feltétel

Egy elágazás vagy egy ciklus esetén a végrehajtás menetét befolyásoló logikai kifejezés.

folyamatábra

Egy grafikus algoritmus megjelenítési technika, melyben a különböző jellegű tevékenységek eltérő alakzatokban vannak megjelenítve és ezeket nyilakkal kötjük össze a végrehajtás menetének meghatározása céljából.

inkrementálás

Egy olyan értékadás, mely során egy változó értéke a korábbi értékhez képest eggyel nő.

kifejezés

Operátorokból, operandusokból és zárójelekből álló formula, képlet.

konstans

Egy a program szövegébe „égetett” érték, mely csak a program átírásával változtatható meg. Egy változó értékét többek között egy konstans, azaz literál segítségével is megadhatjuk. Például: x=96, ebben az esetben a 96 egy konstans.

logikai kifejezés

Olyan kifejezés, melynek az értéke vagy igaz vagy hamis. Többnyire feltételekben szerepel ilyen kifejezés.

operandus

Egy érték, amelyen egy műveletet végrehajtunk.

operátor

Egy művelet megadására, megjelenítésére szolgál. Például az osztás műveletét a / (perjel) operátor jelzi.

változó

Egy névvel ellátott mennyiség, melynek értékére az adott névvel hivatkozhatunk és ez az érték az értékadás során is megváltoztatható.

3.9. Kérdések, feladatok

• Hogyan dönthető el egy rombuszban szereplő feltételről, hogy az egy elágazáshoz vagy egy ismétléshez tartozik-e? [S301]

• Hogyan változnak az alábbi folyamatábra változóinak értékei a végrehajtás során, ha a bemenetként 60-at adunk meg? Vagyis milyen értékeket vesz fel a két változó? [S302]

  

• Mi lesz a fenti algoritmus kimenete, ha bemenetként először 210-et, majd 32-t végül 143-at adunk meg? Mi az összefüggés a bemenet és a kimenet között? Mire szolgál ez az algoritmus?

• Add meg azt az algoritmust, amely egy pozitív egész számot kap bemenetként, és ha ez a szám páros, akkor a kimenet 1 legyen, egyébként pedig 0!

• Készíts egy olyan folyamatábrát, amely egy 0=ax+b alakú elsőfokú egyenlet megoldási algoritmusát írja le! Bemenetként az egyenletben szereplő a és b értékek szolgálnak és kimenetként szeretnénk megadni azt a x értéket, amely kielégíti az egyenletet.

• Add meg folyamatábra segítségével, a Fibonacci-sorozat 1000-nél kisebb elemeit előállító algoritmust! Ez egy olyan egész számokból álló számsorozat, amelynek első eleme a 0 és második eleme a 1. Minden további eleméről elmondható, hogy egy adott eleme értéke, mindig megegyezik a közvetlenül előtte lévő két elem összegével. Ezek közül kimentként meg kell adnunk a 1000-nél kisebb értékeket.

• Szeretnénk eldönteni egy dátumról, hogy az az adott év hányadik napját jelenti. Készíts folyamatábrát, amely három bemenetet használ fel: év, hónap és nap. Ezek alapján kimenete egyetlen pozitív egész szám. Vedd figyelembe a szökőéveket is! Például 2019.02.04. esetén a kimenet 35 kell legyen, míg 2020.03.01 esetén a helyes kimentet a 61.

• Ha van három adott hosszúságú szakaszunk, nem mindig tudunk belőlük egy háromszöget alkotni. Készíts algoritmust, amely három pozitív számról eldönti, hogy lehet-e ilyen hosszúságú szakaszokból háromszöget szerkeszteni! Ehhez fel kell használnod a háromszög-egyenlőtlenséget, vagyis egy háromszög bármely két oldalhosszának az összege nagyobb kell legyen a harmadik oldal hosszánál.

• A matematikában van egy nevezetes számsorozat, amelyről Collatz megfogalmazott egy sejtést, amit eddig még senki sem tudott bizonyítani. A számsorozat egy tetszőleges pozitív egész számmal kezdődik. Minden további eleme kizárólag az őt megelőző egyetlen elem értékétől függ, a következő módon. Ha egy elem páros, akkor a rákövetkezője ennek fele lesz. Minden páratlan elemet a háromszorosánál eggyel nagyobb érték követ. Folyamatábrával írd le azt az algoritmust, amely egy így definiált számsorozatot eredményez kimenetként! Bementet (amiről feltesszük, hogy egy pozitív egész szám) legyen a sorozat első elem! Az algoritmus végrehajtása akkor érjen véget, ha a sorozat aktuális eleme éppen 1 (mivel innentől kezdve a sorozat ciklikus lesz)! [S309]