2. Az algoritmusokról általában¶

2.1. Az algoritmus fogalma¶

Egy (rész)probléma megoldásának mikéntjét egy eljárási renddel, egy ún. algoritmussal adhatjuk meg. Ez lehet teljesen általános probléma, például hogyan juthatunk el a város A pontjából B pontjába vagy hogyan állítsunk össze egy lapraszerelt bútort, de akár egzakt matematikai esetre is gondolhatunk, amikor is meg kell találnunk azt a számot, amely egy elsőfokú egyenletet igazzá tesz. Mindegyik esetben egy megoldási útmutatóra van szükségünk. Ezt a számítástechnika térhódításával, algoritmus névvel illetjük.

Az algoritmus, tehát jól ismert, megengedett lépésekből, tevékenységekből álló véges utasítássorozat, amelyet követve mindig elérjük a kívánt célt. Megadásához természetesen ismernünk kell az alkalmazható elemei lépéseket, amelyek mindenki számára ugyanazt jelentik. Egy szekrény összeállításánál mondjuk a „Rakd össze!” lépés bizonyára a legtöbb emberszámára nem nyilvánvaló és nem végrehajtható elemi lépés. A „Csavard be a csavart!” utasítás sok ember számára már elég jó leírása az egyik megengedett lépésnek. Azonban még itt is felmerülhetnek kérdések. Átmenő vagy önmetsző csavarról van szó? Csillag csavarhúzót, imbuszkulcsot vagy torx kulcsot kell használni hozzá? Egy nem szakembereknek szánt összeszerelési útmutatóban ezeket az alapvető információkat is meg kell adni.

Minden algoritmusnak rendelkeznie kell bizonyos tulajdonságokkal. Mindegyiket meg kell fogalmazni, meg kell jeleníteni valahogy. Bizonyos esetekben képesnek kell lennünk bizonyos változtatásokat végrehajtani az algoritmuson. Ezekről lesz szó a fejezet hátralévő részében.

2.2. Reprezentációs technikák¶

Felmerülhet a kérdés: Hogyan adhatunk meg egy algoritmust? Ennek egyik legtermészetesebb módja az ún. mondatszerű leírás, ahol az egyes lépéseket egy természetes emberi nyelven (például magyarul) megfogalmazott mondatok sorozatával adjuk meg.

Vegyünk egy konkrét esetet! Meg szeretnénk fogalmazni, hogyan működik a matematikában alkalmazott előjel függvény. Mit jelent tehát az y=sign(x) jelölés? Mi az eredmény? Hogyan kell azt meghatározni? Ha a paraméterként megadott x értéke mondjuk -4,5, akkor mi lesz eredményképpen az y értéke? Ha nem is ismertük korábban ezt a jelölést, akkor az alábbi 3 lépést tartalmazó mondatszerű leírás révén valószínűleg mindenki megérti a jelentését:

Ha x egyenlő nullával, y értéke legyen 0!
Különben ha x nagyobb, mint nulla, y értéke legyen +1!
Minden más esetben a függvény adjon -1 értéket!

Természetesen megfogalmazhatjuk ezt másképpen is anélkül, hogy a jelentés megváltozna.

Ha a bemenet (x) nulla a kimenet (y) is ennyi legyen!
Negatív bemenet esetén a kimenet legyen -1!
Pozitív bemenet esetén a kimenet legyen +1!

Egy probléma megoldására tehát létrehozhatunk teljesen eltérő utasításokból álló, különböző belső szerkezettel bíró algoritmusokat, amelyek mégis azonos módon viselkednek (ugyanarra a bemenetre azonos kimenetet biztosítanak). Ezeket alternatív algoritmus-oknak hívjuk. Ezekre példa a fenti két leírás.

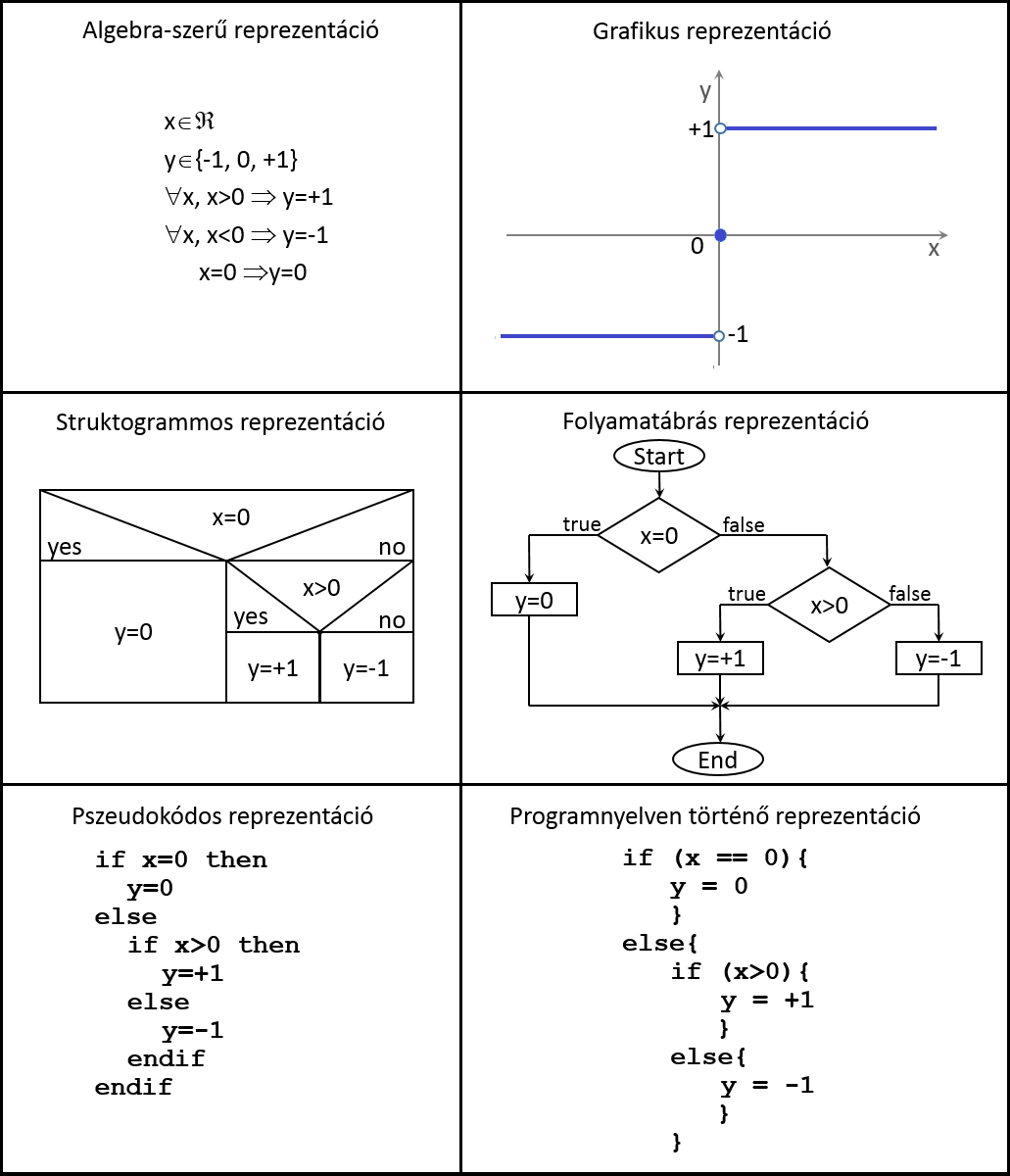
A mondatszerű leíráson kívül számos további megjelenítési módszer, reprezentációs technika terjedt el. A jegyzetnek nem célja ezek teljes körű leírása. A példa kedvéért azonban az alábbi képen megtekinthetünk néhány lehetőséget. Ezek megértése egyelőre nem követelmény, csak a sokféleséget demonstrálják. Mindegyik a fent természetes nyelven megadott algoritmust reprezentálják eltérő módon. A folyamatábra és a pszeudokód a későbbiekben részletes bemutatásra kerül. A valós programozási nyelven történő algoritmus leírással a „Programozási nyelvek 1-2” tárgyak fognak foglalkozni.

2.3. Alapszerkezetek¶

Az algoritmusok háromféle alapszerkezetből épülnek fel:

Szekvencia
Elágazás
Ismétlés

Szekvencia: Az egyes jól ismert elemi lépések egymás utáni sorrendjének megadását jelenti. Ezáltal egyértelművé válik, hogy melyik utasítással kell kezdenünk a végrehajtást, melyik lesz a második, harmadik, stb. lépés. Az i+1. lépés csak akkor kezdhető meg, amikor az i. befejeződött. Szekvencia példa: Tegyél egy tea filtert a csészébe! Majd önts rá forró vizet! Végül ízesítsd cukorral és citromlével!

Elágazás: Akkor használjuk, ha választanunk kell lehetőségek közül, azaz nem biztos, hogy mindig pontosan ugyanazokat a lépéseket hajtjuk végre. Néha például egy adott ponton egy feltételtől függően vagy egyik, vagy másik lépést hajtjuk végre. Előfordulhat persze, hogy bárhogy is döntsünk, egy bizonyos idő után mindenképpen ugyanúgy folytatódik a végrehajtás, a két végrehajtási ág újra összekapcsolódik. Az elágazás tehát az jelenti, hogy vagy az A vagy a B tevékenységet hajtjuk végre, de mind a két esetben ugyanaz a C lépés következik. Egy példa ilyen elágazásra: Ha van futó cipőd húzd fel azt, különben vegyél fel egy kényelmes lábbelit! Ezután menj el kocogni! Bizonyos esetekben vagy megteszünk egy lépést vagy kihagyjuk azt, ami egy speciális esete a kétirányú elágaztatásnak. Példa utóbbi esetre: Menj a bejárati ajtóhoz! Ha zárva van, akkor nyisd ki a zárat! Végül lépj be a házba!

Ismétlés: Egyes problémák megkövetelik azt, hogy egy lépést vagy lépéssorozatot egymás után többször is végrehajtsunk, azaz ciklikusan ismételjünk. Persze valamilyen formában rendelkeznünk kell arról, hogy hányszor történjen meg az ismétlés, mikor lépjünk ki a ciklusból. Természetesen egyértelműen meg kell határoznunk azt is, hogy melyek lesznek az ismétlendő lépések, azaz mi lesz a ciklus magja. Példa ismétlésre: Amíg sótlan a leves, szórd meg kevéske sóval és keverd meg! Egy másik példa: Csinálj 20 fekvőtámaszt!

Ezeknek az alapszerkezeteknek a kombinációi is használhatóak. Elképzelhető például hogy egy elágazás egyik ágában egy újabb lehetőségünk lesz eshetőségek közül választani. Az is gyakran előfordul, hogy egy ismétlésen alapuló lépéssort egy újabb ciklusban többször végrehajtunk, azaz beágyazott ciklust alkalmazunk. Emellett cikluson belül is lehet elágazás vagy elágazáson belül ismétlés, sőt minkét előbbi szerkezet megjelenhet egy algoritmusban egymás után szekvenciálisan. Ilyen összetett szerkezetekkel bármilyen bonyolult algoritmust leírhatunk.

2.4. Az algoritmus tulajdonságai¶

Egy algoritmusnak rendelkeznie kell bizonyos tulajdonságokkal, amelyek nélkül egy utasítássorozat nem is nevezhető algoritmusnak. Ezek a tulajdonságok a teljesség, a végesség, a félreérthetetlenség és a determinisztikusság. Tekintsük át, mit is takarnak ezek a fogalmak!

Teljesség: Egy probléma megoldása során minden eshetőségre rendelkeznünk kell akciótervvel, minden lehetőséget kezelnünk kell. Nem fordulhat elő olyan szituáció, amikor nem tudjuk, mit kell tenni. Tekintsük meg egy helytelen algoritmust a következő problémára!

Hogyan jussunk el a 2. emeletről az 5. emeletre lifttel?

Nyomd meg a lift hívógombját!
Ha megérkezett a lift, szállj be!
Nyomd meg az ‘5’ gombot!
Várj!
Ha az ajtó kinyílik megérkeztél. Szállj ki!

Miért sérti ez a leírás a teljességet? Meg van adva, hogy ha megérkezett a lift be kell szállnunk. Azonban mit tegyünk akkor, ha nem érkezik meg, mert mondjuk elromlott a felvonó? Egy másik nem ennyire szélsőséges szituációban beszállunk, megnyomjuk a gombot, várunk majd az ajtó kinyitása után kiszállunk. Biztos, hogy az 5. emeleten vagyunk? Nincs kezelve az az eset, amikor valaki például a 3. emeleten megállítja a liftet. Ezeket a szálakat el kell varrnunk!

Végesség: Már az algoritmus definíciójában is megjelenik, a „véges utasítássorozat” kifejezés. Lehet, hogy a megoldás néhány lépéssel elérhető, máskor lehet, hogy nagyon sok lépés után kapunk csak eredményt. Azonban a nagyon sok sohasem lehet végtelen sok. Előbb-utóbb az algoritmus véget kell érjen. Egy algoritmus nem tartalmazhat a végtelenségig ismétlődő ciklust. Álljon itt ismét egy rossz utasítássorozat!

Hogyan juthatunk el villamossal a klinikára?

Várj a villamosra!
Ha megjött, szállj fel!
Vegyél jegyet!
Ülj le!
Ha megérkeztél, szállj le!

A várakozás egyfajta ismétlésként fogható fel, de néha a befejezésének feltétele soha nem teljesül, az előfeltételek miatt. Ha nem egy villamos megállóban várunk, akkor a villamos sohasem fog felvenni bennünket. Másrészt nem minden villamos áll meg a klinikánál. Ha rossz villamosra szálltunk a megállóban, akkor a fenti leírás szerint örökre a járművön ragadunk. A lépéssorozat tehát sohasem fejeződik be, az eredményt sohasem érjük el.

Félreérthetetlenség: Egy algoritmus jól ismert elemi lépésekből kell álljon. Nem fordulhat az elő, hogy nem tudjuk, mit is jelent pontosan egy lépés, továbbá az sem megengedett, hogy egy utasítást többféleképpen is értelmezni lehessen. Ellenpélda:

Hogyan készítsünk sült csirkét?

Tedd be a csirkét a sütőbe!
Állítsd be a hőmérsékletet!
Várj, amíg kész lesz!
Szolgáld fel!

Keressünk problémákat! Mi a megfelelő hőmérséklet? 50°C vagy 200°C? Ez a lépés nem egyértelmű egy kezdő számára. (Habár egy profiknak szóló szakácskönyvben ez a lépés akár egy egyértelmű elemi utasítás is lehet.) Másrészt, meddig is kell várni? Mikor van kész a sült csirke? Van, aki jól átsütve szereti, míg más kisé nyersebben. Egyáltalán élő vagy mirelit csirkéről van szó? És ha mirelit, akkor a fólia, amiben van a csirke az csak egy eltávolítandó csomagolás vagy speciális sütőzacskó? A leírás nem egyértelmű, félreértésekhez vezethet.

Determinisztikusság: Egy algoritmusnak azonos feltételek mellett mindig ugyanazt az eredményt kell szolgáltatnia. Nem lehet véletlenszerű, azaz sztochasztikus. Nem lehet 2x2 néha 5. Egy ilyen utasítássorozat nem megbízható. Nézzünk szokás szerint egy hibás leírást!

Hogyan legyünk milliomosok?

Vegyél egy lottót!
Húzd le a kívánt számokat!
Várj a nyereményre (vagy szomorkodj)!

Ez a lépéssorozat, mint tudjuk, néha az elvárt eredményt adja, de más esetekben egyáltalán nem az elvárásoknak megfelelően működik, még akkor sem, ha pontosan követjük az utasításokat. Véletlenszerű (tőlünk független) folyamatoktól is függ az eredmény, ami korlátozza az alkalmazhatóságot.

A fenti négy tulajdonságot mindig szem előtt kell tartanunk egy algoritmus létrehozása során. Legtöbbször kiindulunk egy egyszerű alapötletből, de később rájövünk, hogy ez problémákat vethet fel. Ilyenkor módosítani kell az algoritmuson.

2.5. Egy algoritmus módosításának lehetőségei¶

Egy algoritmus elkészítése során szinte mindig előfordul, hogy változtatnunk kell az eredeti ötleten, mert valamilyen szempontból nem megfelelő működést észlelünk, változnak az igények vagy csak elegánsabb módon szeretnénk elérni a megoldást. Alapvetően négyféle módosítási lehetőséggel élhetünk: általánosítás, kiterjesztés, beágyazás és bolondbiztossá tétel.

Általánosítás: Egy speciális eset kezelése helyett egy szélesebb körű megoldás létrehozására való. Gyakran előfordul, hogy a beégetett konstansok helyett változtatható értékeket használunk így ugyanannak a problémának egy tágabb körét tudjuk kezelni. Vegyünk például egy egyszerű esetet, amikor egy termék nettó ára alapján szeretnénk meghatározni annak bruttó árát.

Deríts ki a nettó árat!
Vedd ennek a 127%-át (27%-os ÁFA kulcsot feltételezve)!
A kapott érték a bruttó ár.

Ez az algoritmus csak 27%-os ÁFA esetén használható, ami elég speciális. Általánosítsuk változtatható ÁFA kulcsot alkalmazva!

Deríts ki a termék nettó árát és ÁFA kulcsát!
Növeld az értéket az aktuális adókulcsnak megfelelően!
A kapott érték a bruttó ár.

Kiterjesztés: Néha rájövünk, hogy bizonyos feltételek eseten a problémák egy teljesen új körét is kezelnünk kell. Ki kell bővítenünk az eddigi algoritmust általában elágazások bevezetésével és az új szituációkat kezelő részalgoritmusok létrehozásával. Egy alkalmazott fizetésének meghatározásához egy cég például használhatja az alábbi algoritmust:

Add meg a ledolgozott órák számát és az órabért!
Szorozd össze az előbbi két értéket!
Vond le az adókat/illetékeket!
Ami marad az a fizetés.

Az a legtöbb egyszerű alkalmazott esetén jól használható módszer, de mi a helyzet a vezetőkkel? Általában ők teljesen más módszertan alapján várnak jövedelmet. Ha őket is szeretnénk kezelni, akkor ki kell terjesztenünk az előbbi algoritmust.

Ha a vezetőről van szó, akkor folytasd a 5. lépésnél, különben menj tovább!
Add meg a ledolgozott órák számát és az órabért!
Szorozd össze az előbbi két értéket!
Folytasd a 6. lépéssel!
A profit felét rendeld a főnökhöz!
Vond le az adókat/illetékeket!
Ami marad az a fizetés.

Ezzel az eredeti algoritmus ki lett terjesztve egy újabb részalgoritmussal.

Beágyazás: Előfordul sokszor, hogy egy nagyobb probléma kisebb részproblémákból áll, amelyeknek a megoldására viszont már korábban hoztunk létre egy jól működő algoritmust. Ilyenkor nem kell mindent elölről kezdenünk, be tudjuk építeni a már meglévő lépéssorozatot az új problémát megoldó algoritmusba. Ez a beágyazás. Máskor ugyanannak a részfeladatnak a megoldására több helyen is szükségünk van egy komplexebb megoldása során. Ilyenkor érdemes a részalgoritmust elszeparálni és szükség esetén csak hivatkozni rá újrafelhasználva azt. A matematikai előjel függvényt megadó alábbi algoritmus már ismerős lehet.

Ha az érték egyenlő nullával, akkor az eredmény legyen 0!
Különben ha az érték nagyobb, mint nulla, az eredmény legyen +1!
Minden más esetben -1 legyen az eredmény!

Ha már tudjuk, hogyan kell egy szám abszolút értékét meghatározni, akkor azt felhasználva (beágyazva) egyszerűsíthetjük a fenti algoritmust.

Ha az érték egyenlő nullával, akkor az eredmény legyen 0!
Különben az eredmény legyen az eredeti érték és a saját abszolút értékének hányadosa!

Persze ehhez szükség van az abszolút érték kiszámítási módjának előzetes ismeretére, itt csak felhasználtuk azt.

Bolondbiztossá tétel: Néha azért kell módosítani egy algoritmust (programot), hogy reagálni tudjon a felhasználó esetleges irreális aktivitására. Amikor egy bemeneti adatot várunk el a felhasználótól készen kell állnunk arra, hogy ez szélsőséges, nem várt választással él vagy olyan adatot ad meg, ami az adott kontextusban nem értelmezhető. Egy program nem állhat le rossz bemeneti érték esetén, hanem ezt fel kell ismernie, tudnia kell reagálni arra is. Ha nincs más megoldás, akkor például egy hibaüzenettel és a megfelelő adat újbóli kérésével. Nézzünk egy egyszerű geometriai példát! A felhasználó megadja bemeneti értékként egy négyzet területét és ez algoritmusnak meg kell mondania a négyzet kerületének hosszát.

Add meg a területet!
Vedd ennek a négyzetgyökét!
A kapott szám 4-szerese lesz a négyzet kerülte. Írd ki ezt!

Ez nem is volt nehéz, gondolhatnánk. Azonban fel kell készülnünk a matematikában nem túl jártas felhasználóra is. Mi történik, ha a felhasználó az 1. utasításban -10 értéket adja meg, mint paramétert. Egy negatív szám négyzetgyöke csak komplex szám lehet, amit viszont nehezen értelmezhetünk kerületként. Az ilyen szituációt kezelhetjük, mondjuk így:

Add meg a területet!
Ha a megadott érték nem negatív, akkor folytasd az 5. lépéssel, különben menj tovább!
Írd ki az alábbi üzenetet: „Hibás adat. Adj meg újat!”
Folytasd az 1. lépésnél!
Vedd ennek a négyzetgyökét!
A kapott szám 4-szerese lesz a négyzet kerülte. Írd ki ezt!

Gyakran fog az előfordulni egy életszerű helyzetben, hogy egy algoritmus bolondbiztossá tétele több erőfeszítést igényel, mint magának az alap algoritmusnak a létrehozása.

Ezek voltak a legfőbb általános gondolatok az algoritmusokkal kapcsolatban. A következő fejezetben a folyamatábra reprezentációs technikával készült algoritmusok révén számos konkrétummal is megismerkedünk.

2.6. Szójegyzék¶

algoritmus: Egy probléma megoldását szolgáltató jól ismert, elemi tevékenységek véges sorozata, amelyet végrehajtva mindig egyértelműen elérjük a kívánt célt.
alternatív algoritmus: Azonos módon viselkedő, de különböző felépítésű algoritmusok.
általánosítás: Valami szükségtelenül specifikus dolog (mint egy konstans érték) lecserélése valami megfelelően általánosra (mint egy változó vagy egy paraméter). Az általánosítás sokoldalúvá teszi a programot a valószínű újrahasznosításhoz, absztrakciót biztosít.
beágyazás: Elszeparált (rész)algoritmusok felhasználása egy komplexebb problémát megoldó algoritmusban.
bolondbiztossá tétel: Az algoritmus felkészítése speciális esetekre, amelyek főként a helytelen felhasználói interakciókból származnak.
determinisztikusság: Egy algoritmusokra jellemző tulajdonság, mely biztosítja a nem sztochasztikus viselkedést, azaz a véletlenszerűségtől mentességet.
elágazás: Egy feltételtől függően kiválasztott utasításcsoport végrehajtás, miközben más utasítások végrehajtását esetleg kihagyjuk.
félreérthetetlenség: Az algoritmusok egyik tulajdonsága, miszerint minden lépésnek egyértelműnek kell lennie a félreértések elkerülése végett.
ismétlés: Tevékenységek többszöri végrehajtása bizonyos körülmények esetén.
kiterjesztés: Az algoritmus kibővítése, mellyel problémák egy újabb körét is meg lehet oldani.
szekvencia: Utasítások egymás után (lépésről-lépésre történő) végrehajtása.
teljesség: Az algoritmusok azon tulajdonsága, mely révén biztosak lehetünk abban, hogy a végrehajtás során előfordulható lehetőségeket kezeltünk.
végesség: Az algoritmusok azon jellemzője, miszerint a lépéssorozat biztosan befejeződik véges időn belül.

2.7. Kérdések, feladatok¶

Értelmezd az alábbi algoritmust! Mit csinál? Mire használható?
1. Adj meg egy egész számot! Nevezzük ezt Y-nak!
2. A D mennyiség értéke legyen 28!
3. Ha az Y szám nem osztható 4-gyel, akkor ugorj a 5. lépésre!
4. Növeld meg a D értékét eggyel!
5. Írd ki a D értékét, mint eredményt!
Szeretnénk meghatározni az A és B egész számok számtani közepét. Melyik algoritmus tulajdonság(ok) nem teljesül(nek) az alábbi lépéssorozatra? [S202]
1. Add meg A és B egész számok értékét!
2. Ha A értéke közelítőleg megegyezik B értékével akkor ugorj a 6. lépésre!
3. Növeld A értékét eggyel!
4. Csökkentsd B értékét eggyel!
5. Folytasd a 2. lépéssel!
6. Az eredmény az A mennyiség értéke. Írd ki!
Adott az alábbi nem tökéletes algoritmus. Meg szeretnéd határozni egy tetszőleges téglalap kerületét. Milyen algoritmus módosításokra van szükség?
1. Add meg az egyik oldal hosszát!
2. Szorozd meg ezt 4-gyel!
3. Írd ki az eredményt!