6. Alprogramok

Rendszeresen előfordul egy programozó munkája során, hogy egy kódrészletet többször is alkalmaznia kell egy programon belül. Jelenlegi tudásunk szerint ilyenkor a kérdéses utasításokat annyiszor le kell írnunk, ahányszor szükségünk van rájuk. Ez nagymértékben csökkenti a fejlesztés hatékonyságát, hosszú kódokat eredményez és fárasztó. Lehetőségünk van arra, hogy egy feladatkört ellátó utasításokat egy egységként kezeljük, megtanítsuk a rendszernek és később csak egy egyszerű elemi lépésként hivatkozzunk rájuk. Technikailag egyszer kell megírnunk a kódot, adnunk kell neki egy nevet és erre a névre bármikor hivatkozhatunk, amikor szükségünk van rá anélkül, hogy újra le kellene írni a lépéssorozatot. Ezek az új, önálló programegységek az ún. alprogram-ok, amelyek a kód újrafelhasználásának eszközei.

Az alprogramoknak van egy nagyon előnyös tulajdonságuk. Tételezzük fel, hogy rendszeresen szükségünk van arra, hogy a kimeneten megjelenítsünk egy Pascal háromszöget. Ha különböző számú szinttel rendelkező háromszögekre van szükségünk, akkor nem szükséges különböző alprogramokat definiálnunk, hanem elég csak egyet, de az személyre szabható kell legyen. Az alprogramok tehát nem csak egy konkrét feladat ellátására szolgának, paraméterek segítségével hasonló feladatok egy szélesebb körét képesek ellátni, tehát nemcsak az algoritmus beágyazást, hanem az általánosítást is megvalósítják.

A programban betöltött szerepük szerint az alprogramoknak két csoportját különítjük el az eljárást és a függvényt. Ezekről lesz szó a következő alfejezetekben.

6.1. Eljárások

Egy bizonyos lépéssorozat végrehajtására szolgál, amely például egy bizonyos kimenetet állít elő. Ezeket a lépések először meg kell „tanítanunk” a rendszer számára, azaz először definiálnunk kell egy adott nevű eljárást, és csak utána tudjuk felhasználni azt. Tegyük fel, hogy rendszeresen szükségünk van arra, hogy a következő sormintát hozzuk létre a kimeneten:

+---+---+---+---+---+

Ebben az esetben definiálhatunk egy minta nevű eljárást a következő pszeudokód részlettel.

   procedure minta()
     i = 1
     while i<=5 do
       output "+"
       j = 1
       while j<=3 do
         output "-"
         j = j+1
       enddo
       i = i+1
     enddo
     output "+"
   end procedure

Mint látható, egy eljárás definíciója mindig a procedure szóval kezdődik és az eljárásnak adandó névvel folytatódik. A névnek egyedinek kell lennie. A nevet egy kerek zárójelpár követi, amelyben az eljárás leendő paramétereit soroljuk fel majd, de jelen esetben mivel nem akarunk paraméterezni ez csak egy üres lista (az zárójel viszont ilyenkor is kötelező). Ezt követi azoknak az utasításoknak a megadása, amelyeket össze akarunk fogni egyetlen egységbe. A definíciót az end procedure szavakkal zárjuk. Megfigyelhető, hogy definíciós utasítások között megadott, az eljárás törzsét alkotó utasítások indentálva vannak. Ezeket a sorokat valahol a pszeudokód elején érdemes elhelyezni és csak a későbbi sorokban hivatkozhatunk rájuk. A pszeudokód további része tehát valahogy így nézhet ki:

   output "Hány méter magas vagy?"
   input magassag
   call minta()
   output "Hány kg súlyú vagy?"
   input suly
   call minta()
   output "A testtömegindexed: ", suly/magassag/magassag
   call minta()

Az eljárás definícióját követően (azzal azonos indentálási szinten) találhatjuk a program további utasításait a 14. sortól kezdve. Nagyon fontos, hogy az alprogramokat tartalmazó pszeudokód végrehajtását nem az első sorral kell kezdeni. A program elején csak egy definíció van, de nem hajtjuk végre azonnal. Az először végrehajtandó utasítás mindig a definíciókon kívüli első sorban található, ami jelenleg a 14. sor. Az egyszerű output és input utasítások után találjuk az ún. eljáráshívó utasítást. Ez a call kulcsszóval kezdődik, amit a hívandó eljárás neve követ, majd ezután találjuk az aktuális paraméterlistát (jelenleg az üres zárójeleket). Ennek a sornak a jelentése az, hogy mielőtt továbbmennél a következő sorra, hajtsd végre a megadott eljárás definíciójában szereplő utasításokat. Azaz csak most rajzolódik ki először a sorminta. Újabb input/output utasítások után megtalálhatjuk az eljárásnak egy újabb hívását, azaz másodjára is lefut az eljárás törzse. Ezt követi a 20. sor, majd az eljárás utasításai harmadjára is végrehajtódnak. Jól látszik az eljárás előnye: nem kell háromszor is leírni a mintát kirajzoló dupla ciklust elegendő csak egy egyszerű, egysoros hívó utasítás. A teljes kimenet így néz ki:

Hány méter magas vagy?
1,8
+---+---+---+---+---+
Hány kg súlyú vagy?
81
+---+---+---+---+---+
A testtömegindexed: 25
+---+---+---+---+---+

Egy másik példán keresztül nézzük meg, mit jelent az alprogramok paraméterezhetősége. A példában az összeadás műveletét csillag karakterek segítségével szeretnénk szemléltetni. Ehhez írnunk kell egy eljárást, amely annyi * karaktert ír ki a kimenetre, amennyire éppen szükségünk van az adott esetben. A paraméterezhető eljárást tartalmazó pszeudokód az alábbi formában adható meg.

   procedure csillagok(db)
     i=1;
     while i<=db do
       output "*"
       i = i+1
     enddo
   end procedure
   output "Adj meg két pozitiv egész számot!"
   input M, N
   call csillagok(M)
   output " + "
   call csillagok(N)
   output " = "
   call csillagok(M+N)

A kód első 7 sora egy csillagok nevű eljárás definíciója, amely paraméterként egy értéket vár el. Ez a formális paraméter, a db változóban lesz eltárolva, értékét egyelőre még nem tudjuk (absztrakció szükséges a megértéséhez). Az eljárás törzsében egy i nevű változó értéke 1-től kezdve fokozatosan növekszik, amíg el nem éri db értékét. Közben persze minden cikluslépésben egy * karakter is megjelenik majd a kimeneten. Ez a definíció. Erre emlékeznünk kell, de végrehajtásra még semmi nem került. Az első igazi tennivaló 8. sor kimeneti utasítása, majd a két szám bekérése az M és N változókba. Ez egyszerűség kedvéért képzeljük el, hogy végrehajtás során a felhasználó a 3 és 2 értékeket fogja bemenetként megadni. A pszeudokód 10. sorában egy eljáráshívás található, ahol az alprogram neve utáni zárójelben az M változó értéke tölti be az aktuális paraméter szerepét. Mielőtt végrehajtanánk az eljárás törzsét megtörténik az ún. paraméterátadás, azaz az M aktuális paraméter jelenlegi értéke (tehát a 3) átmásolódik a formális paramétert jelentő változóba. Végrehajtódik tehát egy rejtett db=3 értékadás. Ezt felhasználva kell végrehajtanunk a törzs lépéseit, megjelenítve tehát 3 darab * karaktert a kimeneten. Az eljárás befejezése után a hívást követő utasítást kell végrehajtani. A pluszjel kiírása után megint egy eljáráshívás történik, csak most az aktuális paraméter (N) érétke, azaz a 2 kerül a db változóba. A program tehát 2 csillag kirajzolása után az egyenlőségjel kiíratásával folytatódik. Az algoritmus egy utolsó eljáráshívással zárul. Az aktuális paraméter most az M és az N változók értékeinek az összege, tehát paraméterátadás során a db változó értéke 5 lesz. Az öt csillag kirajzolásával az eljárás befejeződik és mivel az utóbbi hívás után nincs több utasítás a végrehajtás véget ér. A kimeneten tehát ekkor az alábbi karakterek láthatóak:

*** + ** = *****

6.2. Függvények

Míg az eljárások egy tevékenységet végeznek, addig az alprogramok másik csoportjának, a függvényeknek egy érték előállítása a célja. A paraméterek felhasználásával, egy számítási műveletsor végén kapott eredményt visszajuttat a hívónak. Ez az ún. visszatérési érték, amely nem egyszerűen kiíratódik a kimenetre, hanem visszakerül a függvényhívás helyére, ahol általában egy kifejezésben felhasználásra kerül. Nagyon hasonló ez a matematikai függvény fogalomhoz: A = sin(30) + 1. A szinusz függvény 30 fok esetén a 0,5 értéket képviseli, emiatt az A mennyiség értéke 0,5+1 azaz 1,5 lesz.

A következő példában egy henger térfogatát kiszámoló függvényt is tartalmazó algoritmust láthatunk.

   function henger(sugar, magassag)
     kor_terulet = sugar * 3.14
     terfogat = kor_terulet * magassag
     return terfogat
   end function
   output "Add meg a sugarat!"
   input  R
   output "Add meg a magasságot!"
   input  H
   V = henger(R, H)
   output "A henger ", V, " egység térfogatú."

Egy függvényt hasonlóképpen kell definiálni, mint egy eljárást, csak most a function kulcsszót kell használni. A függvényeknek is van egyedi nevük és formális paraméterlistájuk kerek zárójelek között. A paraméterlista itt is lehet üres, egy vagy több értéket tartalmazó, mint eljárások esetén. Jelenleg két paramétert fogunk használni. A függvény törzse írja le azt absztrakt módon, hogy hogyan kell egy tetszőleges méretű henger térfogatát kiszámolni. Nem elég csak eltárolni az eredményt egy változóba, a függvényben egy speciális utasítással vissza is kell azt juttatni a hívóhoz. Erre szolgál a return kulcsszó és a mögötte megadott egyetlen érték.

A végrehajtás most is a definíciókon kívüli első utasítással kezdődik. Az adatok bekérése és eltárolás után a 10. sorban egy értékadó utasítást találunk a V változó értékét az egyenlőségjel jobb oldalán lévő kifejezés értéke dönti el. A kifejezés most csak egy függvényhívást takar, ahol az aktuális paraméterek értékeit (R és H), mint egyfajta kezdőértéket, megkapják a formális paraméterek (sugar és magassag). Ezek alapján meghatározódik a terfogat értéke, amit a függvény visszaad a hívónak. Logikailag ez olyan, mintha a henger(R, H) hívás az értékadásban kicserélődne a terfogat értékére, amit V eltárol. Ezt már csak egy összetett kiíratás következik és az algoritmus be is fejeződik.

Az előző példában összesen 7 változót használtunk, 4-et (sugar, magassag, kor_terulet, terfogat) az alprogramban és 3-at (R, H, V) a főprogramban, azaz a kód azon részén, ami kívül esik az alprogram definíciókon. Ez a két csoport nem teljesen ugyanúgy viselkedik. Akár függvényről, akár eljárásról van szó az ezekben használt változók az adott alprogram sajátjai. Az adott programegységen kívülről (pl. más alprogramból vagy a főprogramból) nem elérhetőek, nem lehet rájuk hivatkozni. Ennek az oka a hatáskör. Minden változó neve csak egy programegységen belül jelenti ugyanazt a mennyiséget. Ez egyben azt is jelenti, hogy két vagy több külön változónak lehet ugyanaz a neve, csak más programegységben kell lenniük. Ez fokozott figyelmet követel a programozótól, mert amikor például egy A = 23 utasítást ír le, akkor tudnia kell, hogy melyik A változónak ad értéket. Szemléltessük ezt a pszeudokóddal!

   function dupla(N)
     i = 2*N
     return i
   end function
   procedure tobbX(N)
     i = 1
     while i<=N do
       output "X"
       i = i+1
     enddo
   end procedure
   N = 8
   i = 3
   call tobbX(i)
   i = dupla(N)
   output i

Ez a pszeudokód egy 4 soros függvény definícióval kezdődik, ezután láthatunk egy 7 soros eljárás definíciót, amit egy 5 soros főprogram követ. A teljes kódban 6 változót használunk, mivel mindkét alprogramnak és a főprogramnak is van egy N nevű és egy i nevű változója is. Az i mást jelent a 2. sorban, a 6. sorban és a 13. sorban. Ezzel szemben mindegyik i jelölés ugyanazt a változót jelenti mondjuk a 6., 7. és 9. sorokban, mivel ennek hatásköre az eljárás kódja. Természetesen használhattunk volna 6 különböző nevet is a program változóinak, azonban később a valós fejlesztések során nyilvánvalóvá válik, hogy ez nem is olyan egyszerű minden esetben.

Gondoljuk végig, hogyan is történik ennek a kódnak a végrehajtása! Az első két lépésben a főprogram N változója 8 lesz, az i pedig 3. Ezután egy eljáráshívást találunk, ahol az aktuális paraméter értéke (a főprogram i változójának értéke, azaz a 3) átadásra kerül az eljárás formális paraméterébe az N változóban, ám a főprogramban az N továbbra is 8-at jelent. Ez eljárás szintén i nevű változója felveszi az 1, 2 és 3 értékeket, ahogy haladunk az ismétléssel, közben azonban a főprogram i nevű változója változatlanul 3 marad. Az eljárás befejezése után a 15. sorban meg szeretnénk változtatni a főprogram i változójának az értékét. Ehhez szükségünk van a függvény által visszaadott értékre abban az esetben, amikor a paraméter értéke 8. Ez az érték átmásolódik a függvény saját N változójába, majd ennek az értéknek a kétszerese bekerül a függvény i változójába. (Közben természetesen a főprogram változói változatlanok maradnak.) A függvény által kiszámolt és a saját i változóban tárolt 16-os érték ezután visszaadásra kerül a főprogramba, ahol megváltoztatja annak i változóját.

6.3. Eljárás kontra függvény

Amennyiben eddig nem lettek volna elég nyilvánvalóak az eljárások és a függvények közötti különbségek és hasonlóságok, akkor most két egyszerű példa segítségével összegezhetjük őket.

Az első, függvényt használó program pszeudokódja ez:

   function osszeg(szam)
     total = 0
     i = 1
     while i<=szam do
       total = total+i
       i = i+1
     enddo
     return total
   end function
   output "Adj meg egy egész számot!"
   input N
   sum = osszeg(N)
   output "A egész számok összege az adott számig: ", sum

A második program, amely eljárást használ így néz ki:

   procedure osszeg(szam)
     total = 0
     i = 1
     while i<=szam do
       total = total+i
       i = i+1
     enddo
     output "A egész számok összege az adott számig: ", total
   end procedure
   output "Adj meg egy egész számot!"
   input N
   call osszeg(N)

Mindkét esetben, ha bementként 10-et adunk meg a kimenet ez lesz:

A egész számok összege az adott számig: 55

Mi a különbség a két verzió között? Vegyük először az apróbb formai eltéréseket! Az eljárás hívása külön önálló utasítás, míg ezzel szemben a függvényhívás csak egy része egy másik utasításnak (jelen esetben egy értékadásnak). Ráadásul az eljárás hívása során egy speciális kulcsszót (call) is használnunk kell. A függvény törzsében mindig szerepelnie kell egy return kulcsszónak. Ezeknél sokkal jelentősebb különbség, hogy az első kódban az eredmény kiíratását a főprogram végzi el, mivel ő megkapja az eredményt a függvénytől. A második esetben az összeget maga az eljárás írja ki, a főprogram nem is tudja mi lett a végösszeg. Egy eljárás, mint említettük egy tevékenység sorozat elvégzésére szolgál, ami persze lehet számolás is, azonban sok esetben a megfelelő kimenet előállítása a cél. Ezzel ellentétben a függvény célja maga a számolás, az eredmény meghatározása és visszaadása és általában kerülendő az output utasítás használata egy függvény törzsében. Előfordulhat, hogy a számolás eredménye (pl. jelenleg a számok összege) soha nem is jelenik meg kimenetként, csak felhasználjuk ezt az értéket további számításokhoz vagy egyszerűen egy feltételben, egy logikai kifejezés részeként. Ezekben az esetekben függvényt kell használnunk, mert a főprogramnak ismernie kell az eredményt, nem elég, ha az csak a kimeneten van megjelenítve.

Gyűjtsük össze még az egyes alprogram típusok közötti hasonlóságokat is! Mind a függvény, mind az eljárás rendelkezik névvel. Mindkettőjüknek van paraméterlistája, amely lehet akár üres lista, de tartalmazhat egy vagy több paramétert is. Mindegyik alprogram definícióját a pszeudokód elején kell elhelyezni, a főprogram előtt. Egyik alprogram definíciója sem tartalmazhat másik alprogram definíciót. Mindegyik alprogramban használt változónak a hatásköre kizárólag az adott eljárás vagy függvény. Ennek értelmében az alprogramoknak saját változóik vannak, még akkor is, ha két változó neve azonos.

6.4. Rekurzió

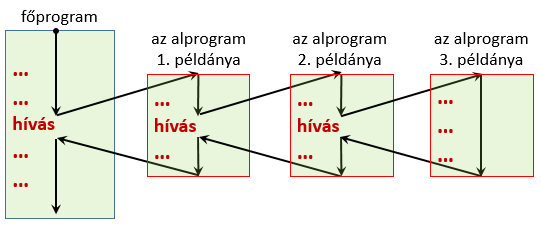
Egy alprogramot nem csak a főprogramból hívhatunk meg, hanem egy másik eljárásból vagy függvényből is, ahogy ez az alábbi pszeudokódban is látható.

   procedure sor(N)
     i = 1
     while i<=N do
       output "X"
       i = i+1
     enddo
   end procedure
   procedure teglalap(A, B)
     j = 1
     while j<=B do
       call sor(A)
       output NEWLINE
       j = j+1
     enddo
   end procedure
   output "Itt egy 3x5 méretű téglalap 'X' karakterekből."
   output NEWLINE
   call teglalap(3,5)
   output "Tetszik?"

A főprogramban az output utasításokon kívül egy teglalap nevű eljárást hívunk meg két paraméterrel. Ebben az eljárásban van egy ciklus, aminek a magja annyiszor fut le, amennyi a második (B) paraméter értéke. A ciklus törzse viszont egy újabb eljárás, a sor meghívását írja elő. A sor törzse tehát többször is lefut úgy, hogy paraméterként megkapja a teglalap eljárás A változójának értékét. Ennek hatására a sor a paraméternek megfelelő számú «X» karaktert jelenít meg a kimeneten. Tehát a téglalap kirajzolásához most a főprogramban hívtunk meg egy alprogramot, ami ciklikus meghívott egy másik alprogramot. Az ilyen egymás utáni alprogram hívások sorozatát hívási láncnak nevezzük.

Azért, hogy teljes legyen a kép, tisztáznunk kell mit jelent az output NEWLINE utasítás. Eddig azt feltételeztük, hogy minden output utasítás a kimeneten közvetlenül egymás után jelenít meg dolgokat. A NEWLINE értékkel kérhetünk egy új sort, azaz egy soremelést, így a következő output utasítás már a következő sorba ír.

Az is előfordulhat, hogy egy alprogram saját magát hívja meg. Az ilyen szituációt rekurzió-nak hívjuk. Ez érdekes helyzeteket eredményezhet és sokszor nagyon hasznos lehet, ezért érdemes vele részletesen is foglalkozni. A hívási láncok mindig a főprogrammal kezdődnek. A rekurzió során ezt egy adott alprogram több példánya követi, tehát még mielőtt befejeznénk, az egyik hívást már belekezdünk ugyanannak az alprogramnak egy újabb hívásába. Természetesen gondoskodnunk kell arról, hogy az egyik alprogrampéldány már ne kezdjen új hívásba, mert különben a hívási lánc végtelen lenne és ugye egy algoritmusnak végesnek kell lennie. Amikor az alprogram egyik példánya befejeződik, visszatérünk az őt közvetlenül meghívó példányba. Tehát az alprogram példányainak befejezése pontosan fordított sorrendben történik, mint azok hívása.

A hívási láncnak az a tulajdonsága, hogy fordított sorrendben bomlik le, mint ahogy felépült nagyon hasznos lehet. Egyes utasítások végrehajtásának a sorrendjét egyszerűen meg tudjuk vele fordítani. Írassuk ki például az egész számokat 1-től 5-ig növekvő sorrendben! Iteratív módon, azaz ciklus segítségével ez egy egyszerű feladat. Az alábbi algoritmus viszont ciklus használata helyett a rekurziót használja fel a működése során.

   procedure szamlalo(N)
     if N>1 then
       call szamlalo(N-1)
     endif
     output N
   end procedure
   output "Számlálás indul:"
   call szamlalo(5)
   output "Számlálás vége."

A végrehajtás a 7. sorban kezdődik egy kimeneti szöveggel, ezután meghívjuk az eljárást az 5 értékkel, mint aktuális paraméterrel. Ennek hatására létrejön a szamlalo eljárás első példánya és abban az N formális paraméter értéke 5 lesz. Az eljárás törzse egy else nélküli if utasítással kezdődik. Mivel a feltétel igaz egy eljáráshívást kell végrehajtanunk. A szamlalo második példánya is elindul saját N változóval. Ennek az értéke 4 lesz, mivel a hívás aktuális paraméter 5-1 volt. Mivel ez az érték is nagyobb, mint 1, aktiválódik az eljárás 3. példánya is (bár még az első kettő sem fejeződött be, csak felfüggesztődött ideiglenesen a végrehajtásuk). Mivel ennek a hívásnak a során az aktuális paraméter 3 volt a harmadik N példány értéke is ennyi lesz. Ennek megfelelően történik az algoritmus további végrehajtása. Tehát mindig újra meghívjuk ugyanazt az eljárást, de mindig egyre kisebb paraméterértékkel. Előbb vagy utóbb a hívás során átadásra kerülő aktuális paraméter értéke 1 lesz. Ennek jelentős a következménye. Az eljárásnak ebben a példányában az elágazás feltétele hamis lesz, azaz nem történik újabb eljáráshívás (nem nő tovább a hívási lánc). A végrehajtás az endif utáni utasítással folytatódik, azaz kiíratódik az N értéke, vagyis az 1. Vegyük észre, hogy ez az első kimenet, amit az alprogramok bármelyike létrehoz. Ezzel a szamlalo alprogram legutóbbi példánya be is fejeződik. Vissza kell térnünk arra a helyre, hol meghívtuk ezt a példányt. A teljes pszeudokódban két helyen történhet meg az eljárás hívása, az a 3. és a 8. sorban. Ha még emlékszünk, akkor a rekurzió során az eljárás saját magát hívta meg, tehát a 3. sorban lévő hívás utáni következő utasítást kell végrehajtanunk. Ez egy output utasítás, ami kiírja N értékét. A változó értéke ebben az eljáráspéldányban 2 volt, tehát ez íratódik ki másodjára. Ezt követően ismét véget ér a szamlalo eljárás aktuális példánya, azaz visszatérünk a hívás (3. sor) utáni következő utasításra és ismét rövidül egy elemmel a hívási lánc. Folytatva az végrehajtást további néhány lépés után már csak egy szamlalo példány marad a hívási láncban (amit legelőször hívtunk meg). Ez kiírja a saját N változója értékét, vagyis az 5 értéket és befejeződik. Vissza kell térnünk az első hívás utáni utasításra. A szamlalo eljárást először a 8. sorban hívtuk meg, tehát már csak a 9. sort kell végrehajtanunk a főprogramban és a teljes program véget ér. A kimeneten láthatjuk 1-től 5-ig az egész számok sorozatát.

Annak, aki most lát először rekurziót, annak valószínűleg sok nehézséget okoz a megértés. Ennek elsődleges oka az, hogy egy alprogramnak több példánya is létezik egyszerre és így számos azonos nevű változót kell fejben nyilván tartani. Elmondhatjuk, hogy a fenti példa iteratív megoldása sokkal egyszerűbb a rekurzív verziónál. Vannak azonban olyan problémák, ahol már maga a feladat megfogalmazása is rekurzív. Gondoljunk csak egy természetes szám faktoriálisának kiszámítására. Ezt a mennyiséget a matematikában gyakran két egyszerű lépésben definiáljuk.

1. Az 1! nem más, mint 1.

2. Minden más N pozitív egész szám faktoriálisa N(N-1)!

Az ennek megfelelő pszeudokód így néz ki.

   function fakt(N)
     if N==1 then
       return 1
     else
       return N*fakt(N-1)
     endif
   end function
   output "Az 5 faktoriálisa ", fakt(5)

A 8. sorban a függvény aktuális paramétere 5, ez kerül be az első hívás N változójába. Mivel az N==1 feltétel hamis az else ág hajtódik végre. Azaz 5!= 5*4!, de ahhoz, hogy vissza tudjuk adni a végeredményt a főprogramnak, tudnunk kell mennyi 4!. Azaz a kifejezés (szorzat) kiértékelését fel kell függesztenünk addig, amíg ki nem találjuk fakt(5-1) értékét. Ekkor tehát létrejön a függvény egy újabb példánya ahol a formális paraméter 4 lesz. Ebben az esetben, a hamis ágban ki kellene számolnunk 4*fakt(4-1) értékét. Ezt azonban csak akkor tudjuk megtenni, ha előbb meghívjuk a függvényt a 3 értékkel, addig tehát ezt a szorzást is felfüggesztjük. A rekurzív hívások hamarosan oda vezetnek, hogy az egyik N példány 1 lesz. Azaz ebből a hívásból 1-gyel térünk vissza. Ekkor visszatérünk a korábban felfüggesztett 2*fakt(1) szorzat kiértékeléséhez, vagyis visszaadjuk az előző függvénypéldánynak a 2 érétket, mivel a fakt(1) hívás ugye 1-et adott vissza. Ez be lesz helyettesítve a 3*fakt(2) szorzat második operandusába, azaz visszaadásra kerül a 6 érték. Előbb-utóbb ismerté válik 4! értéke és a 24 visszakerül a 5*fakt(4) kifejezésbe, aminek eredménye, a 120, végül visszakerül a főprogram output utasításába. Kész is vagyunk.

Bizonyos esetekben a rekurzív megoldás sokkal egyszerűbben leírható, mint az iteratív módszer. Egy viszonylag egyszerű példaként nézzük a számrendszerváltás problémáját. Egy tízes számrendszerben megadott természetes számot kell kettes számrendszerbe átváltani, azaz bináris formában kiíratni. Mondatszerű reprezentációval az alábbi módon is megadhatjuk a szükséges algoritmust.

1. Oszd el a számot 2-vel maradékosan és a maradékot jegyezd meg!

2. Az átváltandó szám a továbbiakban legyen az eredeti szám felének egészrésze!

3. Ha az átváltandó szám nem nulla, akkor folytasd az első lépéssel, különben menj tovább!

4. Írd ki memorizált maradékokat fordított sorrendben!

Az algoritmusban szükségünk lesz egy tört szám egész részének előállítására, vagyis a lefelé kerekítés műveletére. Jelöljük ezt pszeudokódban például a kapcsos zárójelekkel, azaz a {13,982} kifejezés jelentse a 13 értéket. Ha a fenti algoritmust pszeudokóddal akarjuk leírni, akkor egy apró nehézségbe ütközünk. Mit jelent az, hogy „jegyezd meg” illetve az, hogy „írasd ki fordított sorrendben”? A memorizálás itt természetesen változóban való eltárolást jelent. Azonban több változóra is szükségünk lesz, amelyeknek a számát viszont nem tudjuk. Pszeudokódban ilyenkor egyszerű (skalár) változók helyett egy tömb változót kell használnunk. Tömb esetén az egyes értékek fordított sorrendű kiíratása már nem olyan nehéz. Íme tehát a probléma iteratív megoldása, ha a konvertálandó szám a 13 :

   N = 13
   i = 0
   while N!=0 do
     D[i] = N%2
     N = {N/2}
     i = i+1
   enddo
   i = i-1
   while i>=0 do
     output D[i]
     i = i-1
   enddo

Egy jó programozó azonban valószínűleg rekurziót használna tömb és két ciklus alkalmazása helyett. A feladatot megoldó alábbi rekurzív pszeudokód jóval rövidebb.

   procedure konvertal (N)
     if N!=0 then
       call konvertal ({N/2})
       output N%2
     endif
   end procedure
   call konvertal (13)

Ebben az algoritmusban is meghatározzuk a szám felének egészrészét és a kettővel való osztás maradékát is. Utóbbit ki is íratjuk. De hol van az leírva, hogy a maradékokat fordított sorrendben kell kiíratni? Ha alaposan megfigyeljük az eljárás definícióját, láthatjuk, hogy ha szükség van újabb eljáráshívásra, akkor az mindig megelőzi az output utasítást. Mi ennek a következménye? Az adott kiírás csak akkor következik be, ha az előtte meghívott eljárás és minden abból hívott további eljárás befejeződött. Ebben az esetben tehát a később meghívott eljárások kimenetei hamarabb kész lesznek, mint az aktuálisé. Emiatt lesznek a bináris számjegyek fordítva kiíratva a rekurzió révén. Ahhoz, hogy jobban megszokd ezt a gondolkodásmódot, javaslom, hogy papíron hajtsd végre az utóbbi algoritmust több különböző érték esetén is.

6.5. Szójegyzék

aktuális paraméter

Az alprogram hívásakor kerek zárójelben megadott értéklista eleme. A paraméterátadás során ezek az értékek kerülnek át a formális paraméterekbe.

alprogram

Egy programegység, amely az újrafelhasználhatóság és a procedurális absztrakció eszköze a programozásban. Két típusa van: az eljárás és a függvény.

eljárás

Az alprogramok egyik csoportja, melynek célja egy paraméterezhető tevékenységsorozat elvégzése (például egy adott formátumú és tartalmú kimenet előállítása). Hívása külön utasításként történik.

eljáráshívás

Egy call kulcsszóval kezdődő utasítás, amelynek során a paraméterátadás után aktiválódik a megfelelő eljárás kódja.

formális paraméter

Az alprogram definíciójában kerek zárójelben szereplő paraméterlista eleme. Ezek a változók a paraméterátadás során kapnak értéket.

főprogram

A program azon része (programegysége), amely a pszeudokód alprogram definícióin kívül található.

függvény

Az alprogramok egyik típusa, melyeknek célja egy érték előállítása és visszaadása a hívónak, lehetőleg mellékhatás (pl. kimenet előállítása) nélkül.

függvényhívás

Az a folyamat, amelynek révén egy függvény definíciójában szereplő utasításokra kerül a végrehajtás, figyelembe véve az aktuális paramétereket. A folyamat végén a hívás formailag a visszakérési értéket képviseli.

hívási lánc

Függvények és/vagy eljárások hívásának olyan láncolata, amelyben a főprogramban meghívunk egy alprogramot, abban esetleg egy másikat, és így tovább. A meghívott alprogramokból való visszatérés mindig fordított sorrendben történik, mint maguk a hívások.

paraméter átadás

Az a folyamat, amely során az alprogramhívás aktuális paramétereinek értékei megfelelő sorrendben eltárolódnak a formális paramétereket jelentő változókba. Ez egyfajta egyirányú adatcsere a hívótól a hívott alprogram felé.

rekurzió

Egy alprogram hívása egy olyan alprogramból (akár önmagából is), amelyet meghívtak, de még nem ért véget.

visszatérési érték

Az az érték, aminek a meghatározása az adott függvény célja. Formailag ez az érték lecseréli a függvényhívást az adott kifejezésben. Tehát egyfajta adatmozgatás a hívott alprogramtól a hívott felé.

6.6. Kérdések, feladatok

• Mit csinál az alábbi eljárás? Mi a kimenete, ha így hívjuk meg: call foo(42, 35)

     procedure foo(A, B)
       while A!=B do
         if A>B then
           A = A-B
         else
           B = B-A
         endif
       enddo
       output B
     end procedure
  

• Mit csinál az alábbi algoritmus, ha a bemenete 6? Hányszor hívódik meg a függvény? Mi a szerepe a függvénynek? [S602]

     function CHANGE( a )
       return 1-a
     end function
     input Max
     i = 0
     j = 0
     while j<Max do
       i = CHANGE(i)
       j = j+i
       output j
     enddo
     output j
  

• Írj le egy algoritmust pszeudokód segítségével, amely egy 8x8-as méretű négyzetes területre sakktáblaszerűen 0 vagy 1 értékeket írat ki egy eljárás segítségével!

• Módosítsd az előbbi algoritmust, hogy az eljárás tetszőleges NxN-es sakktáblát állítson elő! [S604]

• Írj egy alprogramot tartalmazó pszeudokódot, amely megvalósítja a matematikai abszolút érték függvényt! Hívd is meg ezt a főprogramban egy a felhasználó által megadott értékkel!

• Írj egy algoritmust, amely egy időpont (óra, perc, másodperc) alapján megmondja, hogy az adott időpontig az aktuális napon hány másodperc telt el! Ezt egy függvény segítségével add meg és hívd is meg a függvényt a felhasználó által megadott adatokkal!

• Írj egy eljárást, amely paraméterként megkapja az adott napon eltelt másodpercek számát és megmondja az ennek megfelelő időpontot óra:perc:másodperc formátumban!

• Írj egy pszeudokódot, amely bekér a felhasználótól két számot (B és E) és egy függvény segítségével meghatározz mennyi B-nek az E-edik hatványa! Add meg a függvény kódját, hogy B valós szám, illetve E negatív egész is lehessen! [S608]

• Írj egy háromparaméteres eljárást tartalmazó algoritmust, amely az első paraméterében megadott értéktől kezdve a második paraméterben megadott értékig kiíratja a számokat a harmadik paraméterben megadott lépésközzel!

• Írj egy eljárást, amely kiíratja a 10x10-es szorzótáblát a kimenetre! Módosítsd a pszeudokódot úgy, hogy paraméterezhető legyen az eljárás és tetszőleges NxN-es szerkezetet is ki tudjon írni!

• Írd meg egy függvény definícióját, amelynek első paramétere egy tömb (a tömb neve), második paramétere a tömb elemeinek a száma, a harmadik paramétere egy tetszőleges szám! A függvény az adott tömbben keresse meg a harmadik paraméterként megadott értéket! Ha az érték előfordul a tömbben, akkor térjen vissza az első előfordulás indexével, ellenkező esetben a -1 értékkel! [S611]

• Írj egy algoritmust, amely egy (háromparaméteres) függvény segítségével eldönti, hogy három szám közül melyik a legnagyobb!

• Írj egy eljárást pszeudokóddal, amely egy számokat tartalmazó több elemeit növekvő sorban kiírja a kimenetre! Az eljárásnak első paramétere legyen a tömb (csak a tömb nevét kell leírni), a második paramétere pedig a tömb elemeinek a száma!

• Mit csinál az alábbi algoritmus, ha a bemenete 900? Hányszor hívódik meg a függvény? [S614]

     procedure foo(x,y)
       if x>=y then
         if x%y==0 then
           foo(x/y,y)
           output y
         else
           foo(x,y+1)
         endif
       endif
     end procedure
     input N
     call foo(N, 2)
     output "Ready"