 szimbólummal jelöljük, ahol
szimbólummal jelöljük, ahol
|
Ahhoz, hogy teljesen jellemezzünk egy sorbanállási rendszert, azonosítanunk
kell azt a sztochasztikus folyamatot, amely a beérkező igényeket írja le, és
meg kell adnunk a kiszolgálás szabályait és struktúráját. A beérkező
folyamatot általában az egymás után beérkező igények közötti
időintervallumok valószínűségeloszlása segítségével jellemezhetjük. Ezt az  szimbólummal jelöljük, ahol
szimbólummal jelöljük, ahol
 .
.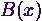 -szel
jelöljük, azaz
-szel
jelöljük, azaz
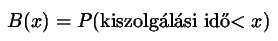 .
.A kiszolgálás szabályára és struktúrájára vonatkozóan további mennyiségeket kell meghatározni. Ilyen jellemző a rendelkezésre álló kiszolgálóegységek (csatornák) száma, valamint a befogadóképesség, ami nem más, mint a kiszolgálóegységben és a várakozási sorban tartózkodó igények maximális száma, amit gyakran végtelennek tekintünk. A kiszolgálási sorrend írja le azt a szabályt, amely szerint a várakozók közül sorra kerülnek az egyes igények kiszolgálás céljából. A leggyakrabban használt kiszolgálási elvek : FIFO (First In - First Out) - érkezési sorrendben; LIFO (Last In - First Out) - fordított sorrendben történő kiszolgálások. Ha a beérkező igényeket bizonyos csoportokba tartozás szerint meg lehet különböztetni, akkor a csoportok között prioritást lehet megállapítani, és ezen a prioritáson alapul a kiszolgálás sorrendje. Ez az egyik legalkalmasabb ütemezési elv, mivel így az igények közötti fontossági sorrendet felállítva történik a kiszolgálás.
A prioritásos sorbanállási elvnek két fő típusa van: abszolút és relatív. Az előbbi azt jelenti, hogy ha egy igény kiszolgálása folyamatban van, és érkezik egy magasabb prioritású igény, akkor a kiszolgálás megszakad, és újra beáll a várakozási sorba. Ha legközelebb rákerül a kiszolgálás, akkor az kezdődhet az elejétől vagy a megszakítás helyétől. A relatív prioritásos esetben a fontosabb igény beérkezésekor a kiszolgálás nem szakad meg, hanem folytatódik, majd a befejezéskor a legfontosabb várakozó igény kiszolgálása kezdődik.
A sorbanállási rendszerek hatékonyságának és teljesítményének vizsgálatához a következő mérőszámokat fogjuk meghatározni: az igények várakozási ideje; a rendszerben levő igények száma; a foglaltsági intervallum hossza (vagyis az a folytonos időintervallum, amelyben a kiszolgáló egység állandóan foglalt); az üresjárati időszakasz hossza; a pillanatnyi munkahátralék eloszlása. Mindegyik mennyiség valószínűségi változó, és így teljes valószínűségszámítási jellemzésüket (vagyis eloszlásfüggvényüket) keressük, amit általában nehéz megadni, így sokszor megelégszünk az átlagos mennyiségekkel.
Az elemi sorbanállási elmélet egyrészt történeti okokból, másrészt pedig azért fontos, mert alkalmas arra, hogy szemléltesse a bonyolultabb sorbanállási rendszerek jellemzőit is.
Egyszerűség kedvéért tekintsünk először egy egykiszolgálós rendszert.
A sorbanállási rendszerek teljesítményének mérésére legalkalmasabb eszköz a
torlódás vizsgálata. Legyen  egy dimenzió nélküli mennyiség, amelyet a
következőképpen lehet definiálni:
egy dimenzió nélküli mennyiség, amelyet a
következőképpen lehet definiálni:
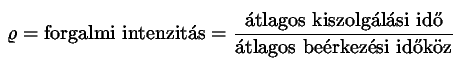 .
. -val, ami nem más, mint az
átlagos beérkezési időköz reciproka, valamint az átlagos kiszolgálási időt
-val, ami nem más, mint az
átlagos beérkezési időköz reciproka, valamint az átlagos kiszolgálási időt 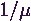 -vel.
Ekkor a következőt kapjuk:
-vel.
Ekkor a következőt kapjuk:
 .
.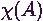 az
az 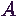 esemény karakterisztikus függvényét, azaz
esemény karakterisztikus függvényét, azaz
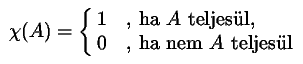 ,
,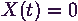 azt az eseményt, hogy a kiszolgáló tétlen
a
azt az eseményt, hogy a kiszolgáló tétlen
a 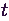 időpillanatban.
Ekkor a szerver időegységre eső kihasználtsága
Ekkor a következőt kapjuk:
időpillanatban.
Ekkor a szerver időegységre eső kihasználtsága
Ekkor a következőt kapjuk:
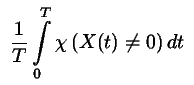 ,
,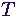 egy elegendően hosszú időintervallum.
Ha
egy elegendően hosszú időintervallum.
Ha  esetén a fenti
mennyiségeknek létezik határértéke, akkor a szerver kihasználtságán ezt az
esetén a fenti
mennyiségeknek létezik határértéke, akkor a szerver kihasználtságán ezt az
 -sel jelölt mennyiséget értjük.
Továbbá 1 valószínűséggel fennáll
-sel jelölt mennyiséget értjük.
Továbbá 1 valószínűséggel fennáll
 ,
, annak stacionárius valószínűsége, hogy a szerver tétlen,
annak stacionárius valószínűsége, hogy a szerver tétlen,
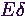 a kiszolgáló egység átlagos foglaltsági periódushosszát,
a kiszolgáló egység átlagos foglaltsági periódushosszát,
 pedig az átlagos tétlenségi periódushosszát jelöli.
pedig az átlagos tétlenségi periódushosszát jelöli.
Ez az összefüggés Markov-folyamatoknál speciális esete a következő, gyakran felhasználható
relációnak. Legyen  egy ergodikus Markov-folyamat,
egy ergodikus Markov-folyamat,
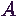 pedig állapotterének
egy részhalmaza. Látható, hogy
pedig állapotterének
egy részhalmaza. Látható, hogy
 az idő folyamán felváltva tartózkodik
az idő folyamán felváltva tartózkodik
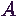 -ban
és
-ban
és 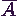 -ban.
Ekkor 1 valószínűséggel
-ban.
Ekkor 1 valószínűséggel
 ,
,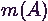 és
és
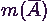 az
az
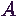 ill. az
ill. az 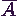 részhalmazban való
átlagos tartózkodási időt jelöli egy ciklus alkalmával,
részhalmazban való
átlagos tartózkodási időt jelöli egy ciklus alkalmával,
 pedig
az
pedig
az  folyamat ergodikus eloszlása.
folyamat ergodikus eloszlása.
Egy  párhuzamos szerverből álló rendszerben
párhuzamos szerverből álló rendszerben 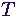 idő alatt átlagosan
idő alatt átlagosan
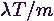 igény érkezik
szerverenként, feltéve, hogy a forgalom egyenletes eloszlású az
igény érkezik
szerverenként, feltéve, hogy a forgalom egyenletes eloszlású az  kiszolgáló
egység között.
Ha minden beérkezett kérés kiszolgálása átlagosan
kiszolgáló
egység között.
Ha minden beérkezett kérés kiszolgálása átlagosan 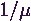 ideig tart, akkor a szerver
teljes foglaltsági idejének várható értéke
ideig tart, akkor a szerver
teljes foglaltsági idejének várható értéke 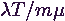 . Osszuk el
ezt a mennyiséget
. Osszuk el
ezt a mennyiséget 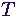 -vel, így
-vel, így
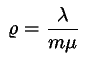 .
. szerveres rendszer
kihasználtsági tényezőre vonatkozó korrekt kifejezés:
szerveres rendszer
kihasználtsági tényezőre vonatkozó korrekt kifejezés:
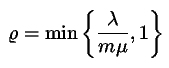 .
.
Másik gyakran használt teljesítménymérő eszköz
a rendszer átbocsátóképességének vizsgálata. Ezt a
mennyiséget úgy definiálhatjuk, mint az időegységenként
kiszolgált igények átlagos számát.  szerveres rendszerben minden időegység alatt
szerveres rendszerben minden időegység alatt  igény kiszolgálása fejeződik be, így az
igény kiszolgálása fejeződik be, így az
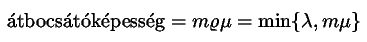 .
. érkezési
intenzitással, amennyiben a
érkezési
intenzitással, amennyiben a  kisebb, mint a maximális kiszolgálási
sebesség (
kisebb, mint a maximális kiszolgálási
sebesség ( ),
azon túl az átbocsátóképesség beáll
),
azon túl az átbocsátóképesség beáll  -re.
-re.
Az igények szempontjából a legjelentősebb teljesítménymérő eszköz az az idő,
amit a várakozási sorban vagy a rendszerben töltenek. Definiáljuk a  várakozási időt, mint a
várakozási időt, mint a 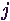 -dik igény várakozási sorban eltöltött idejét,
és a
-dik igény várakozási sorban eltöltött idejét,
és a  válaszidőt, mint az igény által e rendszerben eltöltött
teljes időt. Ezen jelöléseket használva a következő egyenlőséget kapjuk:
válaszidőt, mint az igény által e rendszerben eltöltött
teljes időt. Ezen jelöléseket használva a következő egyenlőséget kapjuk:
 ,
,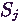 a kiszolgálási időt jelöli.
a kiszolgálási időt jelöli.
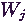 és
és  is valószínűségi változó, várható értékük
is valószínűségi változó, várható értékük  és
és 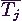 alkalmas a rendszer teljesítményének mérésére.
alkalmas a rendszer teljesítményének mérésére.
A rendszer teljesítményének vizsgálata történhet a várakozási sor hosszának
mérésével is. A 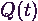 valószínűségi változó jelentse
a
valószínűségi változó jelentse
a 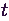 időpillanatban a sorban található igények számát, és
időpillanatban a sorban található igények számát, és  a
a 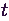 időpillanatban a
rendszerben található igények számát. Egy rendszerben levő igény
vagy a várakozási sorban van, vagy éppen kiszolgálás alatt áll, tehát
időpillanatban a
rendszerben található igények számát. Egy rendszerben levő igény
vagy a várakozási sorban van, vagy éppen kiszolgálás alatt áll, tehát
 szerveres rendszer esetén:
szerveres rendszer esetén:
 .
.Mielőtt rátérnénk az elemi sorbanállási rendszerek vizsgálatára, néhány, Kendalltól származó jelölést vezetünk be, melyek segítségével osztályozhatjuk őket:
A/B/m/K/NHa az említett eloszlások exponenciálisak, akkor az M jelölést használjuk. Továbbá, ha a befogadóképesség vagy az igényforrás számossága végtelen, akkor ezeket a jelöléseket elhagyjuk.
aholA: a beérkezési időközök eloszlásfüggvénye,
B: a kiszolgálási idő eloszlásfüggvénye,
m: a kiszolgálók száma,
K: a rendszer befogadóképessége, azaz a kiszolgálóegységben és a várakozási sorban tartózkodó igények maximális száma,
N: az igényforrás számossága.
Így pl. az M/M/1 rendszer, egy egy kiszolgálós Poisson beérkezéssel és
exponenciális kiszolgálási idővel jellemzett rendszert jelöl.
Az M/G/m rendszernél a beérkezések Poisson-folyamat szerint történnek, a
kiszolgálási idők általános eloszlásúak, és  szerver áll rendelkezésünkre.
Az M/M/r/N/N rendszer esetén az igények egy
szerver áll rendelkezésünkre.
Az M/M/r/N/N rendszer esetén az igények egy  elemű forrásból származnak ahol
exponenciális eloszlású ideig tartózkodnak, a kiszolgálást
elemű forrásból származnak ahol
exponenciális eloszlású ideig tartózkodnak, a kiszolgálást 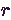 egység végzi
exponenciális eloszlású ideig.
egység végzi
exponenciális eloszlású ideig.
|