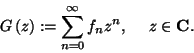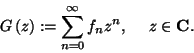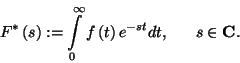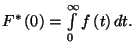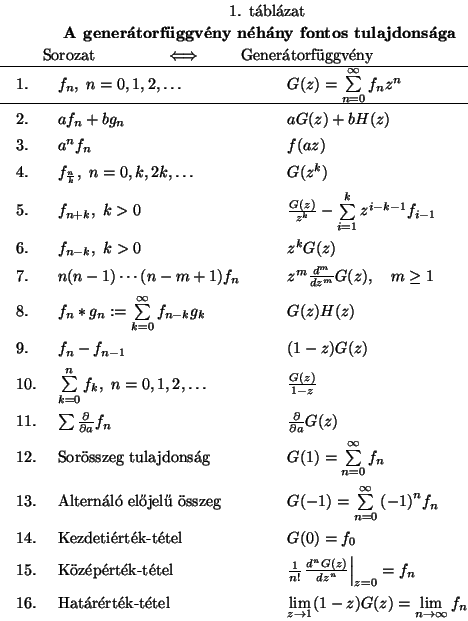Függelék
A függelékben a generátorfüggvény (melyet néha
z-transzformáltnak is nevezünk) és a Laplace-transzformált
néhány olyan tulajdonságát és rájuk vonatkozó
azonosságokat tekintünk át, melyeket a jegyzetbeli levezetések
folyamán -- és általában a sorbanállási elméletben
-- használni lehet. Ezen két transzformált alakja és tulajdonságai
igen hasonlóak. Mindössze alapvető definíciókra és
formulákra szorítkozunk, és talán hasznos is lesz, hogy
a felhasznált nem teljesen alapszintű apparátusról külön
is ejtünk néhány szót. Ajánlott irodalom pl. Karlin-Taylor
(1985), Medhi (1982), Osaki (1992), Rényi (1954, 1966).
A generátorfüggvény
Elsőként foglalkozzunk a generátorfüggvénnyel. Tekintsünk
egy 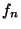 diszkrét idejű függvényt, amely csak a nemnegatív
egész számokra vesz fel nem nulla értéket. Ezt a végtelen
sorozatot szeretnénk jellemezni egyetlen olyan függvénnyel, hogy
abból vissza tudjuk kapni az eredeti sorozatot, ha szükségünk
van rá.
1. Definíció: Legyen
diszkrét idejű függvényt, amely csak a nemnegatív
egész számokra vesz fel nem nulla értéket. Ezt a végtelen
sorozatot szeretnénk jellemezni egyetlen olyan függvénnyel, hogy
abból vissza tudjuk kapni az eredeti sorozatot, ha szükségünk
van rá.
1. Definíció: Legyen 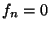 , ha
, ha 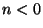 ,
, 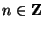 . Az
. Az 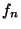 sorozat z-transzformáltja vagy generátorfüggvénye
sorozat z-transzformáltja vagy generátorfüggvénye
Egy sorozatnak létezik generátorfüggvénye, ha a sorozat tagjai
nem nőnek exponenciálisnál gyorsabban, azaz ha létezik 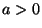 , hogy
, hogy 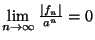 . Egy adott
. Egy adott 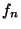 sorozat
sorozat 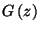 generátorfüggvénye egyértelmű. Jelölés:
generátorfüggvénye egyértelmű. Jelölés:
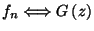 Valószínűségszámítási
problémáknál gyakran kell használnunk a
Valószínűségszámítási
problémáknál gyakran kell használnunk a 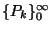 eloszlás
eloszlás 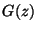 generátorfüggvényét, vagyis ebben az esetben
generátorfüggvényét, vagyis ebben az esetben
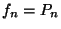 . Ekkor nyilvánvalóan
. Ekkor nyilvánvalóan 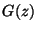 analitikus a
analitikus a 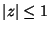 értékekre.
értékekre.
A Laplace-transzformált
A hasonló tulajdonságok miatt ezen szakasz gondolatmenete hasonlít
az előzőéhez. Most azonban folytonos idejű 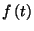 függvényeket tekintünk, melyek a folytonos
függvényeket tekintünk, melyek a folytonos
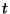 paraméter nemnegatív értékére vesznek csak
fel nullától különböző értékeket. (
paraméter nemnegatív értékére vesznek csak
fel nullától különböző értékeket. ( 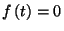 ha
ha 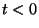 .) Szeretnénk ezt a függvényt úgy transzformálni,
hogy a transzformált egy új komplex változó, mondjuk
.) Szeretnénk ezt a függvényt úgy transzformálni,
hogy a transzformált egy új komplex változó, mondjuk 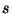 függvénye legyen, ne pedig
függvénye legyen, ne pedig 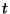 függvénye. Most az
függvénye. Most az 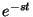 -vel szorozzuk meg a függvényt.
2. Definíció: Legyen
-vel szorozzuk meg a függvényt.
2. Definíció: Legyen 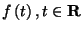 függvény. Ekkor az
függvény. Ekkor az 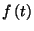 függvény Laplace-transzformáltja
függvény Laplace-transzformáltja
Adott 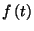 függvény
függvény 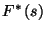 Laplace-transzformáltja egyértelmű. Jelölés:
Laplace-transzformáltja egyértelmű. Jelölés:
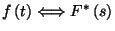 . Ha
. Ha 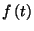 integrálja véges, akkor
integrálja véges, akkor 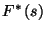 a
a 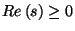 félsíkon analitikus, így
félsíkon analitikus, így 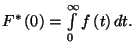
A Laplace-Stieltjes transzformált
3. Definíció Az 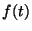 ,
, 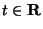 függvény Laplace-Stieltjes transzformáltján
az
függvény Laplace-Stieltjes transzformáltján
az
függvényt értjük. Mivel a Laplace- és Laplace-Stieltjes
transzformáltak nagyon sok hasonló tulajdonsággal rendelkeznek,
mi csak a Laplace-transzformáltra vonatkozó összefüggéseket
soroljuk fel. Fontos speciális eset valamely sűrűségfüggvény
Laplace-transzformáltja. Ez nyilvánvalóan egyben a hozzá tartozó
eloszlásfüggvény Laplace-Stieltjes transzformáltja is. Az
1. ill. 2. táblázatban a generátorfüggvény ill. a Laplace-transzformált
legfontosabb tulajdonságait soroljuk fel. 0pt