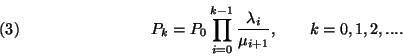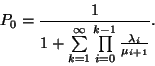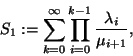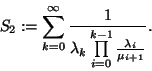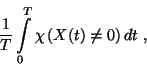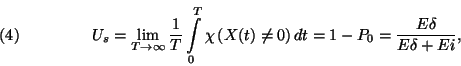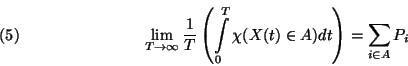II. Elemi sorbanállási elmélet
A sorbanállási elméletre vonatkozó "elemi" jelző azt fejezi
ki, hogy olyan rendszereket vizsgálunk, amelyek tiszta Markov-folyamatok,
és ennek következtében az állapotátmenetek leírására
egyszerű, könnyen kezelhető összefüggéseket kapunk. Az előző
fejezetben azokkal az egyenletekkel foglalkoztunk, amelyek a születési-halálozási
folyamatok abszolút valószínűségeit az időtől függetlenül
írták le. A (3) összefüggés a fejezet lényeges
eredménye; a továbbiakban ennek egyszerű alkalmazásaival foglalkozunk.
A későbbiek során a következőképpen járunk el. Bevezetünk
egy 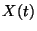 sztochasztikus folyamatot, ami a
sztochasztikus folyamatot, ami a 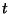 -edik időpillanatban a kiszolgáló egységnél tartózkodó
igényeket jelöli majd. A beérkezési és kiszolgálási
folyamatok eloszlásainak felhasználásával megadjuk a
-edik időpillanatban a kiszolgáló egységnél tartózkodó
igényeket jelöli majd. A beérkezési és kiszolgálási
folyamatok eloszlásainak felhasználásával megadjuk a 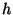 időintervallum alatti átmeneti valószínűségeket.
Ha -- feltevésünk szerint -- a fellépő eloszlások exponenciálisak,
az
időintervallum alatti átmeneti valószínűségeket.
Ha -- feltevésünk szerint -- a fellépő eloszlások exponenciálisak,
az 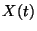 folyamat Markov-típusú lesz, sőt születési-halálozási
folyamat. Konkrét rendszereknél mindig meghatározzuk a születési,
halálozási intenzitásokat, és ezek felhasználásával
megkeressük az egyenletrendszer megoldását. Ezt követően
kiszámítjuk a rendszer működésére vonatkozó jellemzőket
(pl. átlagos sorhossz, kihasználtságok, átlagos várakozási
idő stb.) Az előbbi fejezetben a sztochasztikus folyamatok különböző
osztályait tanulmányoztuk. Kiemeltük, hogy a sorbanállási
rendszerek vizsgálatában alapvető szerepük van a Markov-folyamatoknak.
Ezen belül is egy speciális Markov-folyamatot vizsgáltunk meg
- a születési-halálozási folyamatot. Megmutattuk, hogy a
születési-halálozási folyamatoknak -- a számításokban
-- az az igen ,,jó'' tulajdonságuk van, hogy mind a születések,
mind a halálozások közötti idő exponenciális eloszlású
(ami közvetlen következménye annak, hogy ezek Markov-folyamatok
- feltéve, hogy a rendszer nem üres). Ezután megadtuk a folyamat
állapotegyenleteit. Jelen fejezetben ezeknek az egyenleteknek határátmenet
útján adódó alakjait vizsgáljuk, így a születési-halálozási
sorbanállási rendszerek stacionárius viselkedését
kapjuk meg. Az elemi sorbanállási elmélet egyrészt történeti
okokból, másrészt pedig azért fontos, mert alkalmas arra,
hogy szemléltesse a bonyolultabb sorbanállási rendszerek jellemzőit.
A kapott eredmények betekintést nyújtanak sok egyéb sorbanállási
rendszer viselkedésébe. Nem szabad elfelejtenünk, hogy a születési-halálozási
folyamat miképpen felel meg a sorbanállási rendszereknek. Pl.
tekintsünk egy orvosi várószobát (amelyben esetleg várakozni
kell), és tekintsünk egy orvosi rendelőt, mint egy kiszolgálóegységet.
Minden egyes időpontot, amikor egy páciens belép az utcáról
a várószobába, úgy tekintünk, mint egy igény beérkezését
a sorbanállási rendszerbe; másrészt ezt a beérkezést
úgy is fel lehet fogni, mint egy populáció új tagjának
születését - a populációt a jelenlevő páciensek
alkotják. Hasonlóképpen, amikor (kezelés után) egy
páciens elhagyja a rendelőt, ezt mint a sorbanállási rendszerből
való távozást tekintjük, a születési-halálozási
folyamat terminológiájában ez a populáció egy tagjának
halálát jelenti. A
folyamat Markov-típusú lesz, sőt születési-halálozási
folyamat. Konkrét rendszereknél mindig meghatározzuk a születési,
halálozási intenzitásokat, és ezek felhasználásával
megkeressük az egyenletrendszer megoldását. Ezt követően
kiszámítjuk a rendszer működésére vonatkozó jellemzőket
(pl. átlagos sorhossz, kihasználtságok, átlagos várakozási
idő stb.) Az előbbi fejezetben a sztochasztikus folyamatok különböző
osztályait tanulmányoztuk. Kiemeltük, hogy a sorbanállási
rendszerek vizsgálatában alapvető szerepük van a Markov-folyamatoknak.
Ezen belül is egy speciális Markov-folyamatot vizsgáltunk meg
- a születési-halálozási folyamatot. Megmutattuk, hogy a
születési-halálozási folyamatoknak -- a számításokban
-- az az igen ,,jó'' tulajdonságuk van, hogy mind a születések,
mind a halálozások közötti idő exponenciális eloszlású
(ami közvetlen következménye annak, hogy ezek Markov-folyamatok
- feltéve, hogy a rendszer nem üres). Ezután megadtuk a folyamat
állapotegyenleteit. Jelen fejezetben ezeknek az egyenleteknek határátmenet
útján adódó alakjait vizsgáljuk, így a születési-halálozási
sorbanállási rendszerek stacionárius viselkedését
kapjuk meg. Az elemi sorbanállási elmélet egyrészt történeti
okokból, másrészt pedig azért fontos, mert alkalmas arra,
hogy szemléltesse a bonyolultabb sorbanállási rendszerek jellemzőit.
A kapott eredmények betekintést nyújtanak sok egyéb sorbanállási
rendszer viselkedésébe. Nem szabad elfelejtenünk, hogy a születési-halálozási
folyamat miképpen felel meg a sorbanállási rendszereknek. Pl.
tekintsünk egy orvosi várószobát (amelyben esetleg várakozni
kell), és tekintsünk egy orvosi rendelőt, mint egy kiszolgálóegységet.
Minden egyes időpontot, amikor egy páciens belép az utcáról
a várószobába, úgy tekintünk, mint egy igény beérkezését
a sorbanállási rendszerbe; másrészt ezt a beérkezést
úgy is fel lehet fogni, mint egy populáció új tagjának
születését - a populációt a jelenlevő páciensek
alkotják. Hasonlóképpen, amikor (kezelés után) egy
páciens elhagyja a rendelőt, ezt mint a sorbanállási rendszerből
való távozást tekintjük, a születési-halálozási
folyamat terminológiájában ez a populáció egy tagjának
halálát jelenti. A 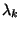 születési és a
születési és a 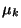 halálozási együtthatók szabad választásával
különféle sorbanállási rendszerek konstruálására
van lehetőségünk, mint ezt rövidesen látni fogjuk. Először
azonban határozzuk meg a stacionárius megoldásokat az általános
esetre.
halálozási együtthatók szabad választásával
különféle sorbanállási rendszerek konstruálására
van lehetőségünk, mint ezt rövidesen látni fogjuk. Először
azonban határozzuk meg a stacionárius megoldásokat az általános
esetre.
 Az előző fejezetben láttuk, hogy a születési-halálozási
folyamatok időtől függő megoldása gyakorlatilag kezelhetetlenné
válik, amint bonyolultabb születési-halálozási
Az előző fejezetben láttuk, hogy a születési-halálozási
folyamatok időtől függő megoldása gyakorlatilag kezelhetetlenné
válik, amint bonyolultabb születési-halálozási 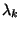 ,
, 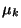 intenzitásokat veszünk. Továbbá, még
ha a
intenzitásokat veszünk. Továbbá, még
ha a 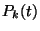 függvényeket meg is tudnánk határozni, nem
világos, mennyire segít minket ez a függvényhalmaz abban,
hogy jobban át tudjuk tekinteni a sorbanállási rendszer viselkedését.
Ezért természetes, hogy azt kérdezzük, vajon a
függvényeket meg is tudnánk határozni, nem
világos, mennyire segít minket ez a függvényhalmaz abban,
hogy jobban át tudjuk tekinteni a sorbanállási rendszer viselkedését.
Ezért természetes, hogy azt kérdezzük, vajon a 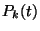 valószínűség�ek
valószínűség�ek 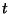 növekedésével megállapodnak-e végül
is (stabilizálódnak-e), megszűnik-e időbeli változásuk, beáll-e
stacionárius állapot. Legyen
növekedésével megállapodnak-e végül
is (stabilizálódnak-e), megszűnik-e időbeli változásuk, beáll-e
stacionárius állapot. Legyen
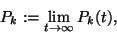
ahol 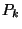 jelenti azon esemény valószínűségét, hogy
a rendszer hosszú működés után a
jelenti azon esemény valószínűségét, hogy
a rendszer hosszú működés után a 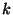 állapotban van. Nagyon fontos, hogy megértsük: jóllehet
a
állapotban van. Nagyon fontos, hogy megértsük: jóllehet
a 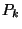 mennyiségek ( feltéve, hogy léteznek ) nem a
mennyiségek ( feltéve, hogy léteznek ) nem a 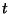 függvényei, ebből nem következik, hogy a határesetben
nem megy át a folyamat az egyik állapotból a másikba. A populáció
tagjainak száma változik az idővel, azonban annak valószínűségét,
hogy a rendszer
függvényei, ebből nem következik, hogy a határesetben
nem megy át a folyamat az egyik állapotból a másikba. A populáció
tagjainak száma változik az idővel, azonban annak valószínűségét,
hogy a rendszer 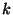 tagú lesz, nagy
tagú lesz, nagy 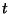 -re éppen
-re éppen 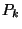 adja meg. Feltételezve, hogy a konstans határérték
létezik, a születési-halálozási folyamatokra felírt
(29, 30) egyenletekben a
adja meg. Feltételezve, hogy a konstans határérték
létezik, a születési-halálozási folyamatokra felírt
(29, 30) egyenletekben a 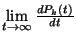 mennyiséget nullával
tehetjük egyenlővé. Ebből azonnal egy lineáris egyenletrendszer
adódik
mennyiséget nullával
tehetjük egyenlővé. Ebből azonnal egy lineáris egyenletrendszer
adódik
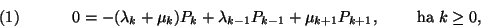
feltételezve, hogy 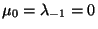 . Megköveteljük, hogy ez a teljes eseményrendszer
is legyen, melyre normalizáló feltételként hivatkozunk majd
:
. Megköveteljük, hogy ez a teljes eseményrendszer
is legyen, melyre normalizáló feltételként hivatkozunk majd
:

Egyensúlyi helyzetben a befelé irányuló folyamnak egyenlőnek
kell lennie a kifelé irányuló folyammal. A 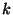 állapotra koncentrálva megfigyelhetjük, hogy - a beáramlás
intenzitása a
állapotra koncentrálva megfigyelhetjük, hogy - a beáramlás
intenzitása a 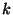 állapotba =
állapotba = 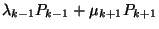 , - a kiáramlás intenzitása
a
, - a kiáramlás intenzitása
a 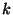 állapotból =
állapotból = 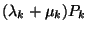 . Egyensúlyi helyzetben ez a két érték
meg kell, hogy egyezzen, így azonnal kapjuk, hogy
. Egyensúlyi helyzetben ez a két érték
meg kell, hogy egyezzen, így azonnal kapjuk, hogy
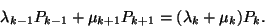
Amint azt az 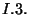 részben láttuk
részben láttuk
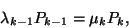
és az általános megoldás könnyen adódik
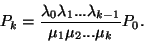
Az összes  valószínűséget az intenzításokkal és
az egyetlen ismeretlen
valószínűséget az intenzításokkal és
az egyetlen ismeretlen 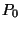 állandóval fejeztük ki:
állandóval fejeztük ki:
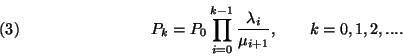
(Az üres szorzat értéke definíció szerint 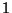 .) A normalizáló feltétel segítségével
meghatározhatjuk a
.) A normalizáló feltétel segítségével
meghatározhatjuk a 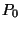 -t, nevezetesen
-t, nevezetesen
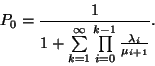
Ez a szorzatalakú megoldás az egyik legfontosabb egyenlete az elemi
sorbanállási elméletnek. Most megvizsgáljuk a 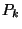 stacionárius valószínűségek létezésének
feltételeit. Pontosabban azt kell megnézni, hogy ezek a mennyiségek
valóban valószínűségeloszlást alkotnak-e. Ehhez viszont
az szükséges, hogy a
stacionárius valószínűségek létezésének
feltételeit. Pontosabban azt kell megnézni, hogy ezek a mennyiségek
valóban valószínűségeloszlást alkotnak-e. Ehhez viszont
az szükséges, hogy a 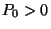 legyen. Ez az egyenletekben szereplő születési és
halálozási együtthatókra ró ki feltételt. Lényegében
azt követeljük meg, hogy a rendszer alkalomadtán üres is legyen.
Az, hogy ez feltétele a stabilitásnak rögtön ésszerűnek
látszik. Pontosabban osztályozhatjuk a lehetőségeket, ha előbb
definiáljuk az alábbi két összeget:
legyen. Ez az egyenletekben szereplő születési és
halálozási együtthatókra ró ki feltételt. Lényegében
azt követeljük meg, hogy a rendszer alkalomadtán üres is legyen.
Az, hogy ez feltétele a stabilitásnak rögtön ésszerűnek
látszik. Pontosabban osztályozhatjuk a lehetőségeket, ha előbb
definiáljuk az alábbi két összeget:
Azt mondjuk, hogy a születési-halálozási folyamat minden egyes
állapota ergodikus, ha
rekurrens nulla, ha
átmeneti (tranziens), ha
Az ergodikus esetben 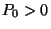 , és ekkor kapjuk a
, és ekkor kapjuk a 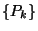 stacionárius valószínűségeket. Ez a legfontosabb
eset számunkra. Az ergodikusság elégséges feltétele teljesül,
ha a
stacionárius valószínűségeket. Ez a legfontosabb
eset számunkra. Az ergodikusság elégséges feltétele teljesül,
ha a 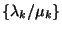 sorozat egy bizonyos
sorozat egy bizonyos  értéktől kezdve végig
értéktől kezdve végig  alatt marad, pontosabban ha létezik valamilyen
alatt marad, pontosabban ha létezik valamilyen 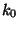 pozitív egész szám és
pozitív egész szám és 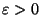 úgy, hogy minden
úgy, hogy minden 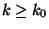 értékre fennáll
értékre fennáll
A legtöbb megvizsgálandó sorbanállási rendszerben teljesül
ez a feltétel.
 Ahhoz, hogy egy sorbanállási rendszert teljesen jellemezzünk, meg
kell adnunk azt a sztochasztikus folyamatot, amely a beérkező igényeket
írja le, és le kell írnunk a kiszolgálás szabályait
és struktúráját. A beérkező folyamatot általában
az egymás után beérkező igények közötti időintervallumok
valószínűségeloszlása segítségével írjuk
le. Ezt az
Ahhoz, hogy egy sorbanállási rendszert teljesen jellemezzünk, meg
kell adnunk azt a sztochasztikus folyamatot, amely a beérkező igényeket
írja le, és le kell írnunk a kiszolgálás szabályait
és struktúráját. A beérkező folyamatot általában
az egymás után beérkező igények közötti időintervallumok
valószínűségeloszlása segítségével írjuk
le. Ezt az 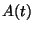 szimbólummal jelöljük, ahol
szimbólummal jelöljük, ahol 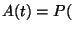 két egymás utáni beérkezési időköz
két egymás utáni beérkezési időköz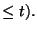
A sorbanállás elméletében többnyire feltesszük,
hogy az egymás utáni beérkezések közötti időközök
(röviden beérkezési időközök), azonos eloszlású
független valószínűségi változók (a beérkezési
folyamat ún.  alkot). A másik sztochasztikus
mennyiség, amit meg kell adni, a beérkező igények által
a feldolgozással szemben támasztott követelmények (munka)
nagysága; ezt kiszolgálási időnek nevezzük és
valószínűségeloszlását
alkot). A másik sztochasztikus
mennyiség, amit meg kell adni, a beérkező igények által
a feldolgozással szemben támasztott követelmények (munka)
nagysága; ezt kiszolgálási időnek nevezzük és
valószínűségeloszlását 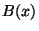 -szel jelöljük, azaz
-szel jelöljük, azaz
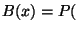 kiszolgálási idő
kiszolgálási idő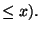
A kiszolgálás ideje annak az időintervallumnak a hosszát jelenti,
amelyet az igény a kiszolgáló egységben eltölt.
A kiszolgálás szabályára és struktúrájára
vonatkozóan további menynyiségeket kell meghatározni. Az
egyik a befogadóképesség, ami nem más, mint a várakozó
sor maximális hossza. Ezt rendszerint 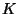 -val jelöljük, és értékét gyakran végtelennek
tekintjük. Egy további jellemző a rendelkezésre álló
kiszolgáló állomások (csatornák) száma.
A kiszolgálási elv adja meg az igények kiszolgálásának
sorrendjét. A leggyakrabban használt kiszolgálási elvek
: FIFO (First In - First Out) - érkezési sorrendben; LIFO (Last In
- First Out) - fordított sorrendben; SIRO (Service In Random Order) - véletlen
sorrendben történő kiszolgálások. Ha a beérkező igényeket
bizonyos csoportokba tartozás szerint meg lehet különböztetni,
és a csoportok között prioritást lehet megállapítani,
akkor ezen a prioritáson alapul a kiszolgálás sorrendje. Ez az
egyik legalkalmasabb ütemezési elv, mivel így az igények
közötti fontossági sorrendet felállítva történik
a kiszolgálás. A prioritásos sorbanállási elvnek két
fő típusa van: abszolút és relatív. Az előbbi
azt jelenti, hogy ha egy igény kiszolgálása folyamatban van,
és érkezik egy magasabb prioritású igény, akkor az
éppen kiszolgálás alatt álló folyamat kiszolgálása
megszakad, és újra beáll a várakozási sorba, míg
a magasabb prioritású kiszolgálása elkezdődik. Relatív
priorításnál a kiszolgálás nem szakad meg, hanem annak
végeztével a kiszolgáló a legmagasabb priorítással
rendelkező igénnyel folytatja munkáját. A számítógéprendszerek
egyik leggyakoribb kiszolgálási elve a TS (Time Sharing) vagy más
terminológiával RR (Round Robin) -- időosztásos diszciplina
--, ami a következőt jelenti. A kiszolgálásra várakozó
jobok mindegyikét a CPU bizonyos
-val jelöljük, és értékét gyakran végtelennek
tekintjük. Egy további jellemző a rendelkezésre álló
kiszolgáló állomások (csatornák) száma.
A kiszolgálási elv adja meg az igények kiszolgálásának
sorrendjét. A leggyakrabban használt kiszolgálási elvek
: FIFO (First In - First Out) - érkezési sorrendben; LIFO (Last In
- First Out) - fordított sorrendben; SIRO (Service In Random Order) - véletlen
sorrendben történő kiszolgálások. Ha a beérkező igényeket
bizonyos csoportokba tartozás szerint meg lehet különböztetni,
és a csoportok között prioritást lehet megállapítani,
akkor ezen a prioritáson alapul a kiszolgálás sorrendje. Ez az
egyik legalkalmasabb ütemezési elv, mivel így az igények
közötti fontossági sorrendet felállítva történik
a kiszolgálás. A prioritásos sorbanállási elvnek két
fő típusa van: abszolút és relatív. Az előbbi
azt jelenti, hogy ha egy igény kiszolgálása folyamatban van,
és érkezik egy magasabb prioritású igény, akkor az
éppen kiszolgálás alatt álló folyamat kiszolgálása
megszakad, és újra beáll a várakozási sorba, míg
a magasabb prioritású kiszolgálása elkezdődik. Relatív
priorításnál a kiszolgálás nem szakad meg, hanem annak
végeztével a kiszolgáló a legmagasabb priorítással
rendelkező igénnyel folytatja munkáját. A számítógéprendszerek
egyik leggyakoribb kiszolgálási elve a TS (Time Sharing) vagy más
terminológiával RR (Round Robin) -- időosztásos diszciplina
--, ami a következőt jelenti. A kiszolgálásra várakozó
jobok mindegyikét a CPU bizonyos 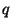 , ú.n. kvantum ideig szolgálja ki. Ha ennyi idő alatt a job
kiszolgálása teljesen befejeződik, akkor távozik a CPU-tól,
ha nem, akkor ismét beáll a várakozók sorába. Ez az
elv azt eredményezi, hogy a rövid CPU időt igénylő jobok nem
tartózkodnak sokáig a CPU-nál. Mivel ezt az elvet elég nehéz
matematikailag modellezni, vagyis megfelelő sztochasztikus folyamatot konstruálni
hozzá, ezért szívesebben foglalkozunk ezen elv határesetével,
amikor is a
, ú.n. kvantum ideig szolgálja ki. Ha ennyi idő alatt a job
kiszolgálása teljesen befejeződik, akkor távozik a CPU-tól,
ha nem, akkor ismét beáll a várakozók sorába. Ez az
elv azt eredményezi, hogy a rövid CPU időt igénylő jobok nem
tartózkodnak sokáig a CPU-nál. Mivel ezt az elvet elég nehéz
matematikailag modellezni, vagyis megfelelő sztochasztikus folyamatot konstruálni
hozzá, ezért szívesebben foglalkozunk ezen elv határesetével,
amikor is a 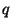 nagyon kicsi. Ekkor kapjuk az ú.n. PS (Processor Sharing) --
osztott processzoros -- kiszolgálási diszciplinát. Ekkor,
ha
nagyon kicsi. Ekkor kapjuk az ú.n. PS (Processor Sharing) --
osztott processzoros -- kiszolgálási diszciplinát. Ekkor,
ha 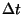 idő alatt
idő alatt 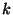 job tartózkodik a CPU-nál, akkor mindegyik kiszolgálása
folyik, de nem
job tartózkodik a CPU-nál, akkor mindegyik kiszolgálása
folyik, de nem 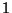 , hanem
, hanem 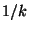 intenzitással. Vagyis
intenzitással. Vagyis 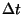 idő alatt mindegyik job igényelt kiszolgálási
idejéből
idő alatt mindegyik job igényelt kiszolgálási
idejéből 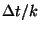 egység telt el.
egység telt el.
A sorbanállási rendszerek hatékonyságának és teljesítményének
vizsgálatához a következő mérőszámokat fogjuk meghatározni:
az  ; a rendszerben levő igények száma; a
; a rendszerben levő igények száma; a  (vagyis az a folytonos időintervallum, amelyben a kiszolgálós
egység állandóan foglalt); az üresjárati időszak
hossza; a pillanatnyi munkahátralék nagysága.
Mindegyik mennyiség valószínűségi változó, és
így teljes valószínűségszámítási jellemzésüket
(vagyis eloszlásfüggvényüket) keressük, amit általában
nehéz megadni, így sokszor megelégszünk az átlagos
menynyiségekkel és szórásokkal. Az elemi sorbanállási
elmélet egyrészt történeti okokból, másrészt
pedig azért fontos, mert alkalmas arra, hogy a bonyolultabb sorbanállási
rendszerek jellemzőit is meg lehessen határozni.
(vagyis az a folytonos időintervallum, amelyben a kiszolgálós
egység állandóan foglalt); az üresjárati időszak
hossza; a pillanatnyi munkahátralék nagysága.
Mindegyik mennyiség valószínűségi változó, és
így teljes valószínűségszámítási jellemzésüket
(vagyis eloszlásfüggvényüket) keressük, amit általában
nehéz megadni, így sokszor megelégszünk az átlagos
menynyiségekkel és szórásokkal. Az elemi sorbanállási
elmélet egyrészt történeti okokból, másrészt
pedig azért fontos, mert alkalmas arra, hogy a bonyolultabb sorbanállási
rendszerek jellemzőit is meg lehessen határozni.
Egyszerűség kedvéért tekintsünk először egy egykiszolgálós
rendszert. A sorbanállási rendszerek teljesítményének
mérésére legalkalmasabb eszköz a torlódás vizsgálata.
Legyen 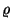 a következő dimenzió nélküli menynyiség:
a következő dimenzió nélküli menynyiség:
Az 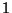 -nél nagyobb forgalmi intenzitás azt mutatja, hogy
az igények gyorsabban érkeznek, mint ahogy egy kiszolgálóegység
(szerver, csatorna) ki tudná szolgálni őket. Jelölje
-nél nagyobb forgalmi intenzitás azt mutatja, hogy
az igények gyorsabban érkeznek, mint ahogy egy kiszolgálóegység
(szerver, csatorna) ki tudná szolgálni őket. Jelölje 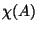 az
az 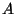 esemény karakterisztikus függvényét, azaz
esemény karakterisztikus függvényét, azaz
és 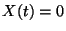 azt az eseményt, hogy a kiszolgáló tétlen
a
azt az eseményt, hogy a kiszolgáló tétlen
a 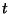 időpillanatban. Ekkor a szerver időegységre eső kihasználtsága
a
időpillanatban. Ekkor a szerver időegységre eső kihasználtsága
a ![$[0,T]$](img430.gif) intervallumon
intervallumon
Ha 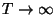 esetén a fenti mennyiségeknek létezik határértéke,
akkor a szerver kihasználtságán ezt az
esetén a fenti mennyiségeknek létezik határértéke,
akkor a szerver kihasználtságán ezt az 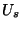 -sel jelölt mennyiséget értjük. Továbbá
-sel jelölt mennyiséget értjük. Továbbá
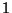 valószínűséggel fennáll
valószínűséggel fennáll
ahol 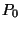 annak stacionárius valószínűsége, hogy a szerver
tétlen,
annak stacionárius valószínűsége, hogy a szerver
tétlen, 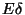 a kiszolgáló egység átlagos foglaltsági
periódushosszát,
a kiszolgáló egység átlagos foglaltsági
periódushosszát, 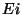 pedig az átlagos tétlenségi periódushosszát
jelöli. (Lásd pl. Cohen (1976, 1982), Ross (1970))
A (4) összefüggés Markov-folyamatoknál speciális esete
a következő, gyakran felhasználható relációnak. Legyen
pedig az átlagos tétlenségi periódushosszát
jelöli. (Lásd pl. Cohen (1976, 1982), Ross (1970))
A (4) összefüggés Markov-folyamatoknál speciális esete
a következő, gyakran felhasználható relációnak. Legyen
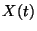 egy ergodikus Markov-folyamat,
egy ergodikus Markov-folyamat, 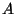 pedig diszkrét állapotterének egy részhalmaza.
pedig diszkrét állapotterének egy részhalmaza.
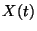 az idő folyamán felváltva tartózkodik
az idő folyamán felváltva tartózkodik 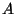 -ban és
-ban és 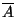 -ban. Ekkor
-ban. Ekkor 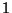 valószínűséggel
valószínűséggel
ahol 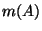 és
és 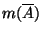 az
az 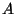 ill. az
ill. az 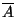 részhalmazban való átlagos tartózkodási
időt jelöli egy visszatérés alkalmával,
részhalmazban való átlagos tartózkodási
időt jelöli egy visszatérés alkalmával, 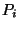 pedig az
pedig az 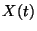 folyamat ergodikus eloszlása. (Lásd Tomkó (1981,
1982)) Egy
folyamat ergodikus eloszlása. (Lásd Tomkó (1981,
1982)) Egy 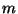 párhuzamos szerverből álló rendszerben
párhuzamos szerverből álló rendszerben 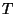 idő alatt átlagosan
idő alatt átlagosan 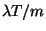 igény érkezik szerverenként, feltéve,
hogy a forgalom egyenletesen kerül elosztásra az
igény érkezik szerverenként, feltéve,
hogy a forgalom egyenletesen kerül elosztásra az 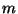 kiszolgáló egység között. Ha minden beérkezett
kérés kiszolgálása átlagosan
kiszolgáló egység között. Ha minden beérkezett
kérés kiszolgálása átlagosan 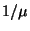 ideig tart, akkor egy szerver teljes foglaltsági idejének
várható értéke
ideig tart, akkor egy szerver teljes foglaltsági idejének
várható értéke 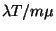 , így
, így
Mivel a kihasználtság maximum 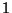 lehet, így az
lehet, így az 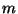 szerveres rendszer kihasználtsági tényezőre vonatkozó
korrekt kifejezés:
szerveres rendszer kihasználtsági tényezőre vonatkozó
korrekt kifejezés:
Másik gyakran használt teljesítménymérő mutató a
számítógépes rendszerek sorbanállási modelljének
analízisében a rendszer átbocsátóképessége.
Ezt a mennyiséget úgy definiálhatjuk, mint az időegységenként
kiszolgált igények átlagos számát. 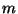 szerveres rendszerben minden időegység alatt átlag
szerveres rendszerben minden időegység alatt átlag 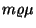 igény kiszolgálása fejeződik be, így
az
igény kiszolgálása fejeződik be, így
az
Ami azt jelenti, hogy az átbocsátóképesség ekvivalens
a 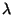 érkezési intenzitással, amennyiben a
érkezési intenzitással, amennyiben a 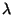 kisebb, mint a maximális kiszolgálási sebesség
(
kisebb, mint a maximális kiszolgálási sebesség
(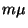 ), azon túl az átbocsátóképesség beáll
), azon túl az átbocsátóképesség beáll
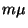 -re.
-re.
Az igények szempontjából a legjelentősebb teljesítménymérő
eszköz az az iidő, amit egy igény a várakozási sorban vagy
a rendszerben tölt. Definiáljuk a 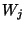 várakozási időt, mint a
várakozási időt, mint a 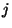 -edik igény várakozási sorban eltöltött idejét,
és a
-edik igény várakozási sorban eltöltött idejét,
és a 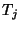 válaszidőt, mint az igény által e rendszerben
eltöltött teljes időt. Ezen jelöléseket használva a
következő egyenlőséget kapjuk:
válaszidőt, mint az igény által e rendszerben
eltöltött teljes időt. Ezen jelöléseket használva a
következő egyenlőséget kapjuk:
ahol 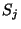 a kiszolgálási időt jelöli.
a kiszolgálási időt jelöli. 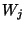 és
és 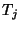 is valószínűségi változó, várható
értékük
is valószínűségi változó, várható
értékük 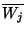 és
és 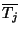 alkalmas a rendszer teljesítményének mérésére.
A rendszer teljesítményének vizsgálata történhet
a várakozási sor hosszának mérésével is.
A
alkalmas a rendszer teljesítményének mérésére.
A rendszer teljesítményének vizsgálata történhet
a várakozási sor hosszának mérésével is.
A 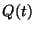 valószínűségi változó jelentse a
valószínűségi változó jelentse a 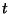 időpillanatban a sorban található igények számát,
és
időpillanatban a sorban található igények számát,
és 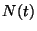 a
a 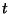 időpillanatban a rendszerben található igények számát.
Egy rendszerben levő igény vagy a várakozási sorban van, vagy éppen
kiszolgálás alatt áll, tehát
időpillanatban a rendszerben található igények számát.
Egy rendszerben levő igény vagy a várakozási sorban van, vagy éppen
kiszolgálás alatt áll, tehát 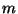 szerveres rendszer esetén:
szerveres rendszer esetén:
Mielőtt rátérnénk az elemi sorbanállási rendszerek vizsgálatára,
néhány, Kendalltól származó jelölést vezetünk
be, melyek segítségével osztályozhatjuk a rendszereket. A
következő jelölés általánosan használt: N/A/B/m/K,
ahol
N: az igényforrások száma, A: a beérkezési időközök
eloszlásfüggvénye, B: a kiszolgálási idő eloszlásfüggvénye,
m: a kiszolgálók száma, K: a várakozási sor kapacitása.
Ha az A és B eloszlások exponenciálisak, akkor az M jelölést
(Markov) használjuk. Továbbá, ha a befogadóképesség
és az igényforrás számossága végtelen, akkor ezeket
a jelöléseket elhagyjuk. Így pl. az M/M/1 szimbólum, egy
egy kiszolgálós Poisson beérkezéssel és exponenciális
kiszolgálási idővel jellemzett rendszert jelöl. Az M/G/m rendszernél
a beérkezések Poisson-folyamat szerint történnek, a kiszolgálási
idők általános eloszlásúak, és 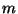 szerver áll rendelkezésünkre. Az N/M/M/r rendszer esetén
az igények
szerver áll rendelkezésünkre. Az N/M/M/r rendszer esetén
az igények 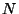 forrásból származnak ahol exponenciális eloszlású
ideig tartózkodnak, a kiszolgálást
forrásból származnak ahol exponenciális eloszlású
ideig tartózkodnak, a kiszolgálást 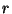 egység végzi exponenciális eloszlású ideig.
egység végzi exponenciális eloszlású ideig.