I.3. Születési-halálozási folyamatok
A Markov-folyamatok egy igen fontos speciális osztálya születési és
halálozási folyamatok néven ismert. A definiáló feltétel:
minden állapotból csak ,,szomszédos'' állapotba mehet végbe
átmenet (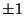 -el változhat). Állapottérnek ekkor a nem negatív
egész számok halmazát választjuk (ami nem megy az általánosság
rovására), és
-el változhat). Állapottérnek ekkor a nem negatív
egész számok halmazát választjuk (ami nem megy az általánosság
rovására), és 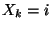 esetében
esetében 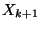 vagy
vagy 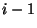 , vagy
, vagy 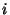 , vagy
, vagy 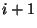 lehet. A születési-halálozási folyamatoknak
nagy szerepük van a sorbanállási rendszerek vizsgálatában.
Ahhoz, hogy egy
lehet. A születési-halálozási folyamatoknak
nagy szerepük van a sorbanállási rendszerek vizsgálatában.
Ahhoz, hogy egy 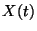 Markov lánc születési-halálozási folyamat
legyen, ki kell elégítenie az alábbi feltételeket :
Markov lánc születési-halálozási folyamat
legyen, ki kell elégítenie az alábbi feltételeket :
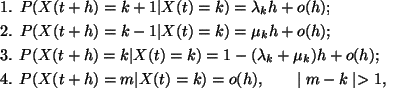
ahol 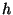 egy tetszőlegesen kis intervallumot jelent,
egy tetszőlegesen kis intervallumot jelent, 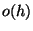 pedig olyan mennyiséget jelöl, amely gyorsabban tart
pedig olyan mennyiséget jelöl, amely gyorsabban tart
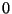 -hoz, mint
-hoz, mint 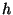 , ha
, ha 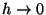 , vagyis
, vagyis 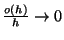 , ha
, ha 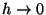 . Vegyük észre, hogy
. Vegyük észre, hogy 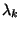 ,
, 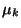 pozitív mennyiségek függetlenek az időtől. A
pozitív mennyiségek függetlenek az időtől. A 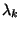 -kat születési intenzitásnak, a
-kat születési intenzitásnak, a 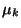 -kat pedig halálozási intenzitásnak nevezzük. Jelöljük
-kat pedig halálozási intenzitásnak nevezzük. Jelöljük
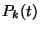 -vel annak valószínűségét, hogy a folyamat
a
-vel annak valószínűségét, hogy a folyamat
a 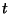 időpillanatban a
időpillanatban a 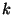 állapotban van, vagyis
állapotban van, vagyis
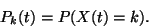
Ezt szokás abszolút valószínűségnek is nevezni. Ezen valószínűségek
kiszámításához figyelembe kell venni a következőket.
A 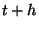 időpillanatban a
időpillanatban a 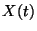
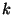 állapotban van akkor és csak akkor, ha az alábbi feltételek
teljesülnek:
1.
állapotban van akkor és csak akkor, ha az alábbi feltételek
teljesülnek:
1. 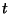 időpillanatban a folyamat a
időpillanatban a folyamat a 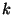 állapotban van és a
állapotban van és a 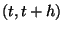 időintervallumban változás nem következik be;
2.
időintervallumban változás nem következik be;
2. 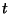 időpillanatban a folyamat a
időpillanatban a folyamat a 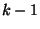 állapotban volt és a
állapotban volt és a 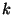 -ba történt átmenet; 3.
-ba történt átmenet; 3. 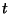 időpillanatban a folyamat a
időpillanatban a folyamat a 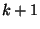 állapotban volt és a
állapotban volt és a 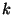 -ba történt átmenet; 4.
-ba történt átmenet; 4. 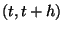 alatt 2 vagy több átmenet történt. Látható,
hogy az 1-3 feltételek kölcsönösen kizárják egymást,
és a 4. eset valószínűsége
alatt 2 vagy több átmenet történt. Látható,
hogy az 1-3 feltételek kölcsönösen kizárják egymást,
és a 4. eset valószínűsége 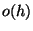 . Világos, hogy
. Világos, hogy 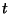 minden értékére teljes eseményrendszerről van
szó, így:
minden értékére teljes eseményrendszerről van
szó, így:

Az előbbi feltételek teljesülése után már felírhatjuk
a 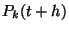 valószínűséget:
valószínűséget:
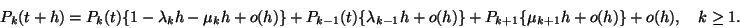
Ha mindkét oldalból kivonjuk 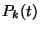 -t és osztjuk
-t és osztjuk 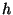 -val, akkor
-val, akkor 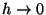 esetén a következő differenciálegyenleteket kapjuk:
esetén a következő differenciálegyenleteket kapjuk:
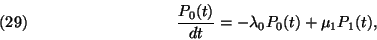
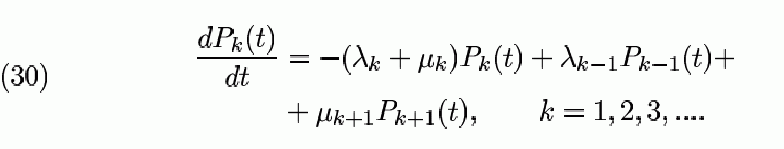
Annak belátása, hogy a fenti egyenleteknek létezik egyértelműen
meghatározott megoldása nem könnyű feladat. Az egyenletrendszer
megoldható, ha bizonyos megkötéseket teszünk a születési-halálozási
folyamatra vonatkozóan. Meg kell adni a 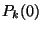 ,
, 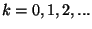 értékeket, ezenkívül a (28) egyenlőségnek
is teljesülnie kell.
értékeket, ezenkívül a (28) egyenlőségnek
is teljesülnie kell.
Most tegyünk egy kis kitérőt. Adjunk egy intuitív módszert
arra, hogyan lehet az előbbi differenciálegyenlet-rendszert megkapni. Figyeljük
a 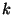 állapotot. Észrevehetjük, hogy oda csak a
állapotot. Észrevehetjük, hogy oda csak a 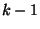 és a
és a 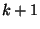 állapotokból lehet átlépni. Hasonlóképpen
a
állapotokból lehet átlépni. Hasonlóképpen
a 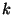 állapototë csak úgy lehet elhagyni, hogy a
állapototë csak úgy lehet elhagyni, hogy a 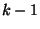 vagy a
vagy a 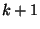 állapotba jutunk. Mivel dinamikus szituációt vizsgálunk,
ezért világos, hogy a két rátának a különbsége,
amellyel a folyamat belép a
állapotba jutunk. Mivel dinamikus szituációt vizsgálunk,
ezért világos, hogy a két rátának a különbsége,
amellyel a folyamat belép a 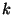 állapotba, ill. elhagyja azt, egyenlő kell, hogy legyen az illető
állapot abszolút valószínűségének a megváltozásával.
Ennek segítségével leírhatjuk a
állapotba, ill. elhagyja azt, egyenlő kell, hogy legyen az illető
állapot abszolút valószínűségének a megváltozásával.
Ennek segítségével leírhatjuk a 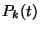 valószínűségekre vonatkozó mozgásegyenletet.
A
valószínűségekre vonatkozó mozgásegyenletet.
A 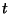 pillanatban az érkezés intenzitása ebbe az állapotba:
pillanatban az érkezés intenzitása ebbe az állapotba:
míg a távozás intenzitása:
E kettő különbsége az abszolút valószínűség
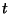 -beli változásával (deriváltjával) egyenlő,
azaz
-beli változásával (deriváltjával) egyenlő,
azaz
De ez éppen a (30) összefüggés 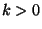 esetén. Könnyű belátni, hogy ez az érvelés
a
esetén. Könnyű belátni, hogy ez az érvelés
a 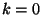 esetben is korrekt egyenletre vezet. Az általános, időfüggő
megoldás nehezen adható meg, ezért mi megelégszünk az
ún.
esetben is korrekt egyenletre vezet. Az általános, időfüggő
megoldás nehezen adható meg, ezért mi megelégszünk az
ún.  (vagy stacionárius) megoldással, mivel ez
sok esetben jól használható. Definiáljuk a stacionárius megoldást,
mint egy
(vagy stacionárius) megoldással, mivel ez
sok esetben jól használható. Definiáljuk a stacionárius megoldást,
mint egy 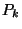 valószínűségi eloszlást, amelyre fennáll
a következő:
valószínűségi eloszlást, amelyre fennáll
a következő:  . Ha egy ilyen eloszlás létezik, akkor egyértelmű
és minden
. Ha egy ilyen eloszlás létezik, akkor egyértelmű
és minden 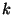 -ra teljesül:
-ra teljesül:
Mivel minket most csak a folyamat időtől független tulajdonságai érdekelnek,
ezért először vegyük a (30) baloldalának határértékét
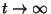 esetén, ez
esetén, ez 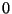 -val lesz egyenlő, és egy kis átalakítással a következő
lineáris differenciaegyenletet kapjuk:
-val lesz egyenlő, és egy kis átalakítással a következő
lineáris differenciaegyenletet kapjuk:
Ebből arra következtethetünk, hogy
A (29)-ből:
Tehát a fenti konstansnak nullának kell lenni, ezzel az alábbi
egyenlőségre jutottunk:
Ez a következőképpen értelmezhető: a baloldal a 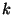 állapotból a
állapotból a 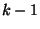 állapotba való átmenet rátája, ami egyensúlyban
van a
állapotba való átmenet rátája, ami egyensúlyban
van a 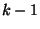 állapotból a
állapotból a 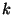 állapotba való átmenet rátájával, ami
a jobboldalon található. Így az egyensúlyi állapot valószínűségei
a következők:
állapotba való átmenet rátájával, ami
a jobboldalon található. Így az egyensúlyi állapot valószínűségei
a következők:
ahol
és
A 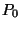 valószínűséget egyértelműen meghatározhatjuk,
mivel a valószínűségek
valószínűséget egyértelműen meghatározhatjuk,
mivel a valószínűségek  összegének
összegének 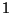 -nek kell lenni. Tehát, ha az
-nek kell lenni. Tehát, ha az
sor konvergens, és összege 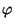 akkor
akkor
és ez egyben a stacionáris eloszlás létezésének
elégséges feltétele is.
A Poisson folyamat: A vizsgált rendszerek közül
a legegyszerűbb a tiszta születési folyamat. Ekkor feltesszük,
hogy 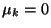 minden
minden 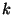 esetén. Tovább egyszerűsítve a problémát
tegyük fel, hogy
esetén. Tovább egyszerűsítve a problémát
tegyük fel, hogy 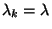 ,
, 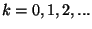 . Ekkor a (29, 30) a következőre redukálódik:
. Ekkor a (29, 30) a következőre redukálódik:
Az egyszerűség kedvéért tegyük fel, hogy a rendszer a 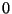 állapotból indul a
állapotból indul a 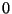 időpillanatban, azaz
időpillanatban, azaz
Könnyű látn<i, hogy a 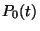 valószínűségre:
valószínűségre:
Így a 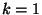 esetre az alábbit kapjuk:
esetre az alábbit kapjuk:
Ennek a differenciálegyenletnek a megoldása:
Indukcióval folytatva a megoldást, könnyen meggyőződhetünk,
hogy
Ez a híres Poisson-eloszlás. A konstans 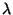 születési intenzitású tiszta születési
folyamatban előforduló születések sorozatát nevezik Poisson
folyamatnak. Mivel a kapott eredményeket később a sorbanállási
rendszerek tanulmányozásakor szeretnénk felhasználni, így
rögtön sorbanállási jelöléseket vezetünk be:
a Poisson-folyamatot mint igények beérkezését tekintjük
valamilyen kiszolgálási rendszerben, nem pedig mint egy populáció
új tagjainak születését. Ezért
születési intenzitású tiszta születési
folyamatban előforduló születések sorozatát nevezik Poisson
folyamatnak. Mivel a kapott eredményeket később a sorbanállási
rendszerek tanulmányozásakor szeretnénk felhasználni, így
rögtön sorbanállási jelöléseket vezetünk be:
a Poisson-folyamatot mint igények beérkezését tekintjük
valamilyen kiszolgálási rendszerben, nem pedig mint egy populáció
új tagjainak születését. Ezért 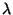 az igénybeérkezés átlagos intenzitása.
A kezdeti feltételllel együtt a
az igénybeérkezés átlagos intenzitása.
A kezdeti feltételllel együtt a 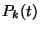 mennyiség megadja annak valószínűségét,
hogy
mennyiség megadja annak valószínűségét,
hogy 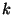 igény érkezik be a
igény érkezik be a 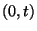 intervallumban. Világos, hogy ha átlagosan
intervallumban. Világos, hogy ha átlagosan 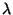 igény érkezik be időegységenként, ezért
egy
igény érkezik be időegységenként, ezért
egy 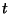 hosszúságú intervallum alatt átlagosan
hosszúságú intervallum alatt átlagosan 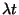 számú igénynek kell beérkeznie, azaz a
számú igénynek kell beérkeznie, azaz a
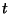 idő alatt beérkezett igények számának várható
értéke
idő alatt beérkezett igények számának várható
értéke 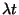 . A Poisson-folyamatot, mint tiszta születési folyamatot
vezettük be, és levezettük a
. A Poisson-folyamatot, mint tiszta születési folyamatot
vezettük be, és levezettük a 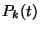 mennyiségekre - egy adott
mennyiségekre - egy adott 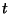 hosszúságú időintervallum alatt bekövetkező érkezések
számának valószínűségeloszlására - egy formulát.
Vizsgáljuk most meg a beérkezések időpillanatainak együttes
eloszlását, ha előre ismert, hogy éppen
hosszúságú időintervallum alatt bekövetkező érkezések
számának valószínűségeloszlására - egy formulát.
Vizsgáljuk most meg a beérkezések időpillanatainak együttes
eloszlását, ha előre ismert, hogy éppen 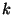 igény érkezett ebben az intervallumban. Osszuk fel a
igény érkezett ebben az intervallumban. Osszuk fel a 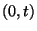 intervallumot
intervallumot 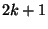 diszjunkt részre a következőképpen. Az
diszjunkt részre a következőképpen. Az 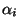 hosszúságú intervallumok előzzék meg a
hosszúságú intervallumok előzzék meg a
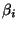 hosszúságú intervallumokat
hosszúságú intervallumokat 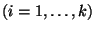 , és az utolsó intervallum
, és az utolsó intervallum 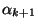 hosszúságú legyen, továbbá
hosszúságú legyen, továbbá
Jelentse 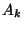 azt az eseményt, hogy éppen egy beérkezés fordul
elő minden egyes
azt az eseményt, hogy éppen egy beérkezés fordul
elő minden egyes 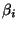 intervallumban
intervallumban 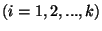 , az
, az 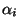 intervallumban pedig egy sem.
intervallumban pedig egy sem. 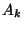 valószínűségét akarjuk kiszámolni, feltéve,
hogy éppen
valószínűségét akarjuk kiszámolni, feltéve,
hogy éppen 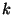 beérkezés történik a
beérkezés történik a 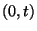 intervallumban. A feltételes valószínűség
definíciójából
intervallumban. A feltételes valószínűség
definíciójából
Amikor a Poisson-folyamat szerinti beérkezéseket vizsgáljuk diszjunkt
időintervallumokban, akkor független eseményeket vizsgálunk, azaz
ezek együttes valószínűségét az egyes valószínűségek
szorzataként lehet kiszámolni. Könnyu látni, hogy
és
Kihasználva ezt, azonnal kapjuk a következőt:
Másrészt tekintsünk egy olyan folyamatot, amelynél a 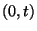 intervallumban
intervallumban 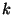 darab pont fordul elő egymástól függetlenül, mégpedig
mindegyik az intervallumon egyenletes eloszlás szerint. Könnyen belátható,
hogy
darab pont fordul elő egymástól függetlenül, mégpedig
mindegyik az intervallumon egyenletes eloszlás szerint. Könnyen belátható,
hogy
ahol a 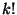 tényező amiatt jelenik meg, mert nem különböztetjük
meg a
tényező amiatt jelenik meg, mert nem különböztetjük
meg a 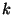 darab pont permutációit. Észrevehetjük, hogy a
(31) és a (32) összefüggésekben megadott két feltételes
valószínűség megegyezik, és ennek alapján arra gondolhatunk,
hogy ha a Poisson-folyamatban
darab pont permutációit. Észrevehetjük, hogy a
(31) és a (32) összefüggésekben megadott két feltételes
valószínűség megegyezik, és ennek alapján arra gondolhatunk,
hogy ha a Poisson-folyamatban 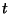 idő alatt
idő alatt 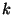 beérkezés történik, akkor a beérkezések
eloszlása ugyanaz, mint
beérkezés történik, akkor a beérkezések
eloszlása ugyanaz, mint 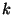 darab ugyanazon az intervallumon egyenletes eloszlású pont
eloszlása. Ennek pontos igazolása a fenti gondolatmenet finomításával
elvégezhető. A születési folyamat tulajdonságaiból könnyű
levezetni, hogy a Poisson-folyamat homogén; vagyis ha
darab ugyanazon az intervallumon egyenletes eloszlású pont
eloszlása. Ennek pontos igazolása a fenti gondolatmenet finomításával
elvégezhető. A születési folyamat tulajdonságaiból könnyű
levezetni, hogy a Poisson-folyamat homogén; vagyis ha 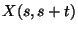 jelöli a
jelöli a 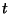 hosszúságú
hosszúságú 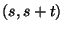 intervallum alatti beérkezések számát, akkor
intervallum alatti beérkezések számát, akkor
függetlenül attól, hogy hol helyezkedik el az intervallum (vagyis
függetlenül az intervallum 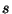 kezdőpontjától).
kezdőpontjától).
Most a Poisson-folyamat és az exponenciális eloszlás közötti
összefüggés vizsgálatára térünk át.
Az exponenciális eloszlásnak szintén központi szerepe van
a sorbanállás elméletében. Tekintsük a 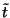 valószínűségi változót - a két
egymás utáni ,,szomszédos'' beérkezések között
eltelt idő -, amelynek eloszlás- és sűrűségfügvényét
valószínűségi változót - a két
egymás utáni ,,szomszédos'' beérkezések között
eltelt idő -, amelynek eloszlás- és sűrűségfügvényét
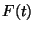 , ill.
, ill. 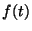 jelöli. Ekkor
jelöli. Ekkor 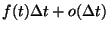 a valószínűsége annak, hogy
a soron következő beérkezésig a legutolsó beérkezéstől
eltelt idő legalább
a valószínűsége annak, hogy
a soron következő beérkezésig a legutolsó beérkezéstől
eltelt idő legalább 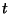 , de legfeljebb
, de legfeljebb 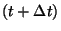 . Mivel
. Mivel 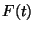 a valószínűsége annak, hogy a beérkezések
közötti idő
a valószínűsége annak, hogy a beérkezések
közötti idő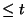 , ezért
, ezért
De 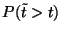 éppen annak valószínűsége, hogy
egyetlen beérkezés sem következik be a
éppen annak valószínűsége, hogy
egyetlen beérkezés sem következik be a 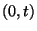 intervallumon, azaz
intervallumon, azaz 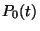 . Azt kapjuk tehát, hogy
. Azt kapjuk tehát, hogy
így az eloszlásfüggvény (a Poisson esetben)
Ezt differenciálva, a sűrűségfüggvény:
Ez a jól ismert exponenciális eloszlás, tehát a 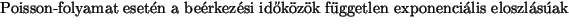 .
Az exponenciális eloszlás legfontosabb jellemzője az, hogy emlékezetnélküli,
azaz a valószínűségi változó múltja nem játszik
szerepet jövőjének meghatározásában. Ezen a következőt
értjük. Képzeljük el, hogy a
.
Az exponenciális eloszlás legfontosabb jellemzője az, hogy emlékezetnélküli,
azaz a valószínűségi változó múltja nem játszik
szerepet jövőjének meghatározásában. Ezen a következőt
értjük. Képzeljük el, hogy a 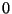 időpillanatban következett be egy beérkezés. Ha azt
kérdezzük, hogy mi a legközelebbi beérkezésig eltelő
időpillanatban következett be egy beérkezés. Ha azt
kérdezzük, hogy mi a legközelebbi beérkezésig eltelő
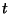 idő eloszlása, a felelet nyilvánvaló, a (33) képlet
adja meg az eloszlásfüggvényét. Teljék el bizonyos idő,
mondjuk
idő eloszlása, a felelet nyilvánvaló, a (33) képlet
adja meg az eloszlásfüggvényét. Teljék el bizonyos idő,
mondjuk 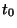 másodperc, ez alatt ne történjen beérkezés.
Ekkor újra megkérdezhetjük: Mennyi a valószínűsége
annak, hogy a legközelebbi beérkezésig mostantól számítva
másodperc, ez alatt ne történjen beérkezés.
Ekkor újra megkérdezhetjük: Mennyi a valószínűsége
annak, hogy a legközelebbi beérkezésig mostantól számítva
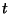 idő telik el. Ez a kérdés csak annyiban különbözik
a
idő telik el. Ez a kérdés csak annyiban különbözik
a 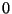 időpillanatban feltett kérdéstől, hogy most tudjuk, a két
beérkezés között eltelő idő legalább
időpillanatban feltett kérdéstől, hogy most tudjuk, a két
beérkezés között eltelő idő legalább 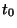 másodperc. Ahhoz, hogy feleljünk a második kérdésre,
a következő számításokat végezzük:
másodperc. Ahhoz, hogy feleljünk a második kérdésre,
a következő számításokat végezzük:
A (33) miatt
és így
Az eredmény azt mutatja, hogy ha az utolsó beérkezés óta
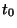 idő telt el, akkor a következő beérkezésig hátralevő
idő eloszlása ugyanaz, mint a beérkezési időköz feltétel
nélküli eloszlása. És ez az egyetlen olyan folytonos eloszlás,
amely ilyen tulajdonságú.
idő telt el, akkor a következő beérkezésig hátralevő
idő eloszlása ugyanaz, mint a beérkezési időköz feltétel
nélküli eloszlása. És ez az egyetlen olyan folytonos eloszlás,
amely ilyen tulajdonságú.
Nem nehéz belátni, hogy
Ez nyilván egyenértékű a
állítással, amelyet a L'Hospital-szabállyal egyszerűen bebizonyíthatunk.
Hiszen
Az 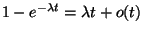 egyenlőség a későbbiekben
nagyon fontos lesz számunkra.
egyenlőség a későbbiekben
nagyon fontos lesz számunkra.
![]() -el változhat). Állapottérnek ekkor a nem negatív
egész számok halmazát választjuk (ami nem megy az általánosság
rovására), és
-el változhat). Állapottérnek ekkor a nem negatív
egész számok halmazát választjuk (ami nem megy az általánosság
rovására), és ![]() esetében
esetében ![]() vagy
vagy ![]() , vagy
, vagy ![]() , vagy
, vagy ![]() lehet. A születési-halálozási folyamatoknak
nagy szerepük van a sorbanállási rendszerek vizsgálatában.
Ahhoz, hogy egy
lehet. A születési-halálozási folyamatoknak
nagy szerepük van a sorbanállási rendszerek vizsgálatában.
Ahhoz, hogy egy ![]() Markov lánc születési-halálozási folyamat
legyen, ki kell elégítenie az alábbi feltételeket :
Markov lánc születési-halálozási folyamat
legyen, ki kell elégítenie az alábbi feltételeket : 

![]() állapotot. Észrevehetjük, hogy oda csak a
állapotot. Észrevehetjük, hogy oda csak a ![]() és a
és a ![]() állapotokból lehet átlépni. Hasonlóképpen
a
állapotokból lehet átlépni. Hasonlóképpen
a ![]() állapototë csak úgy lehet elhagyni, hogy a
állapototë csak úgy lehet elhagyni, hogy a ![]() vagy a
vagy a ![]() állapotba jutunk. Mivel dinamikus szituációt vizsgálunk,
ezért világos, hogy a két rátának a különbsége,
amellyel a folyamat belép a
állapotba jutunk. Mivel dinamikus szituációt vizsgálunk,
ezért világos, hogy a két rátának a különbsége,
amellyel a folyamat belép a ![]() állapotba, ill. elhagyja azt, egyenlő kell, hogy legyen az illető
állapot abszolút valószínűségének a megváltozásával.
Ennek segítségével leírhatjuk a
állapotba, ill. elhagyja azt, egyenlő kell, hogy legyen az illető
állapot abszolút valószínűségének a megváltozásával.
Ennek segítségével leírhatjuk a ![]() valószínűségekre vonatkozó mozgásegyenletet.
A
valószínűségekre vonatkozó mozgásegyenletet.
A ![]() pillanatban az érkezés intenzitása ebbe az állapotba:
pillanatban az érkezés intenzitása ebbe az állapotba:

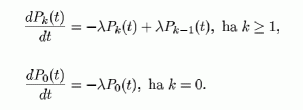
![]() valószínűségi változót - a két
egymás utáni ,,szomszédos'' beérkezések között
eltelt idő -, amelynek eloszlás- és sűrűségfügvényét
valószínűségi változót - a két
egymás utáni ,,szomszédos'' beérkezések között
eltelt idő -, amelynek eloszlás- és sűrűségfügvényét
![]() , ill.
, ill. ![]() jelöli. Ekkor
jelöli. Ekkor ![]() a valószínűsége annak, hogy
a soron következő beérkezésig a legutolsó beérkezéstől
eltelt idő legalább
a valószínűsége annak, hogy
a soron következő beérkezésig a legutolsó beérkezéstől
eltelt idő legalább ![]() , de legfeljebb
, de legfeljebb ![]() . Mivel
. Mivel ![]() a valószínűsége annak, hogy a beérkezések
közötti idő
a valószínűsége annak, hogy a beérkezések
közötti idő![]() , ezért
, ezért 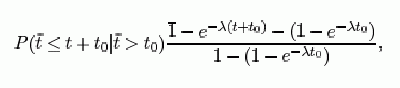
![]() egyenlőség a későbbiekben
nagyon fontos lesz számunkra.
egyenlőség a későbbiekben
nagyon fontos lesz számunkra.