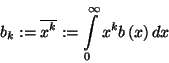III. Középfokú sorbanállási elmélet
III.1. Az M/G/1 rendszer
A sorbanállási elmélet elemeinek megismerését megkönnyíti
az állapot leírás egyszerűsége, különösen az,
hogy a rendszer teljes múltját összefoglalja a pillanatnyilag jelen
lévő igények száma. A Markov-típusú rendszer jövőbeli
viselkedése szempontjából minden más múltbeli információ
lényegtelen. A jól ismert 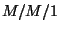 rendszerben mind a beérkezési, mind a kiszolgálási
folyamat Markov típusú (exponenciális eloszlású). Az
rendszerben mind a beérkezési, mind a kiszolgálási
folyamat Markov típusú (exponenciális eloszlású). Az
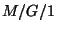 rendszernél viszont a kiszolgálás általános
eloszlású, következésképpen új problémákba
ütközünk, és ezekre más megoldási módszereket
kell találnunk. A jegyzetben a Palm-tól, Takácstól és
Kendall-tól származó, úgynevezett beágyazott Markov-láncok
módszerét fogjuk alkalmazni. Az
rendszernél viszont a kiszolgálás általános
eloszlású, következésképpen új problémákba
ütközünk, és ezekre más megoldási módszereket
kell találnunk. A jegyzetben a Palm-tól, Takácstól és
Kendall-tól származó, úgynevezett beágyazott Markov-láncok
módszerét fogjuk alkalmazni. Az 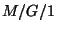 rendszerben egyetlen kiszolgálóegység van, a beérkezési
folyamat
rendszerben egyetlen kiszolgálóegység van, a beérkezési
folyamat 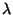 paraméterű Poisson-folyamat, azaz a beérkezési
időközök
paraméterű Poisson-folyamat, azaz a beérkezési
időközök 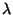 paraméterű exponenciális eloszlású valószínűségi
változók. A kiszolgálási idő eloszlása tetszőleges lehet,
eloszlásfüggvényét
paraméterű exponenciális eloszlású valószínűségi
változók. A kiszolgálási idő eloszlása tetszőleges lehet,
eloszlásfüggvényét 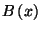 , sűrűségfüggvényét
, sűrűségfüggvényét 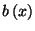 ,
, 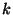 -adik momentumát
-adik momentumát
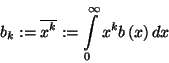
jelöli. Próbáljuk meg leírni az 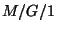 rendszer állapotait! Ha egy bizonyos
rendszer állapotait! Ha egy bizonyos 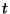 időpontban a rendszer egész múltját akarjuk összefoglalni,
akkor először is meg kell adnunk a
időpontban a rendszer egész múltját akarjuk összefoglalni,
akkor először is meg kell adnunk a 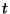 pillanatban a rendszerben tartózkodó igények
pillanatban a rendszerben tartózkodó igények 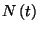 számát, valamint azt, hogy a kiszolgálócsatornában
lévő igény kiszolgálása már mennyi időt vett igénybe
a
számát, valamint azt, hogy a kiszolgálócsatornában
lévő igény kiszolgálása már mennyi időt vett igénybe
a 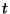 pillanatig; jelölhetjük ezt
pillanatig; jelölhetjük ezt 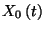 -vel. Ez utóbbi amiatt szükséges, mert
a kiszolgálási idő eloszlása nem feltétlenül emlékezetnélküli.
(Viszont a beérkezési folyamat emlékezetnélküli, ezért
az utolsó beérkezéstől eltelt időt nem kell megadnunk.) Így
az
-vel. Ez utóbbi amiatt szükséges, mert
a kiszolgálási idő eloszlása nem feltétlenül emlékezetnélküli.
(Viszont a beérkezési folyamat emlékezetnélküli, ezért
az utolsó beérkezéstől eltelt időt nem kell megadnunk.) Így
az 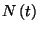 nem Markov-folyamat. Azonban az
nem Markov-folyamat. Azonban az ![$\left[N\left(t\right), X_0\left(t\right)\right]$](img1052.gif) vektor már az,
és ezt tekinthetjük az
vektor már az,
és ezt tekinthetjük az 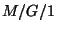 rendszer állapotvektorának, hiszen tartalmazza a múltnak
a folyamat jövőbeli alakulása szempontjából lényeges
részét. Az
rendszer állapotvektorának, hiszen tartalmazza a múltnak
a folyamat jövőbeli alakulása szempontjából lényeges
részét. Az 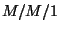 rendszer esetén elég
rendszer esetén elég 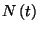 -t megadni, és így egy diszkrét állapotterű
Markov-láncunk van, ahol az állapotok száma megszámlálható.
Jelen esetben a kétdimenziós állapotleírás esetén
az
-t megadni, és így egy diszkrét állapotterű
Markov-láncunk van, ahol az állapotok száma megszámlálható.
Jelen esetben a kétdimenziós állapotleírás esetén
az 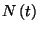 megszámlálható ugyan, de az
megszámlálható ugyan, de az 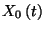 folytonos, és ez megnehezíti a vizsgálatot.
folytonos, és ez megnehezíti a vizsgálatot.