Problémák
1. Tekintsünk egy tiszta Markov-féle sorbanállási rendszert,
amelyben
a, Keressük meg a rendszerben tartózkodó igények számának
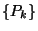 stacionárius eloszlását! b, Milyen összefüggésnek
kell fennállnia a paraméterek között ahhoz, hogy a rendszer
stabilis legyen, vagyis az egyensúlyi helyzetet valóban el lehessen
érni? Interpretáljuk a választ a rendszer dinamikájának
fogalmaival!
2. Tekintsünk egy Markov-típusú sorbanállási rendszert,
amelyben
stacionárius eloszlását! b, Milyen összefüggésnek
kell fennállnia a paraméterek között ahhoz, hogy a rendszer
stabilis legyen, vagyis az egyensúlyi helyzetet valóban el lehessen
érni? Interpretáljuk a választ a rendszer dinamikájának
fogalmaival!
2. Tekintsünk egy Markov-típusú sorbanállási rendszert,
amelyben
a, Fejezzük ki 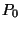 segítségével annak
segítségével annak 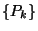 stacionárius valószínűségeloszlását,
hogy
stacionárius valószínűségeloszlását,
hogy 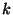 igény van a rendszerben! b, Adjunk formulát a
igény van a rendszerben! b, Adjunk formulát a 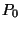 valószínűségre!
3. Tekintsünk egy
valószínűségre!
3. Tekintsünk egy 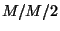 sorbanállási rendszert, amelyben a beérkezések
intenzitása
sorbanállási rendszert, amelyben a beérkezések
intenzitása 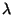 igény másodpercenként, az átlagos kiszolgálási
idő
igény másodpercenként, az átlagos kiszolgálási
idő 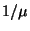 másodperc, ahol
másodperc, ahol 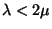 . a, Határozzuk meg azt a differenciálegyenletet,
amelyet a
. a, Határozzuk meg azt a differenciálegyenletet,
amelyet a 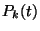 időfüggő valószínűségek kielégítenek!
b, Számítsuk ki a
időfüggő valószínűségek kielégítenek!
b, Számítsuk ki a 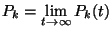 valószínűségekből
álló stacionárius eloszlást!
4. Tekintsünk egy születési-halálozási folyamatot a következő
intenzitásokkal:
valószínűségekből
álló stacionárius eloszlást!
4. Tekintsünk egy születési-halálozási folyamatot a következő
intenzitásokkal:
a, Keressük meg a 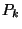 mennyiségeket.
mennyiségeket. 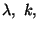 és
és 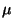 segítségével fejezzük ki őket! b,Határozzuk
meg a rendszerbeli igények számának várható értékét!
5. Felhasználva, hogy
segítségével fejezzük ki őket! b,Határozzuk
meg a rendszerbeli igények számának várható értékét!
5. Felhasználva, hogy
és
bizonyítsuk be, hogy ha 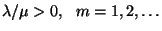 akkor
akkor
6. Az 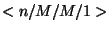 rendszernél határozzuk meg az érkezési
pillanatokban a stacionárius eloszlást, majd ennek felhasználásával
az igények várakozási és tartózkodási idejének
sűrűség- ill. eloszlásfüggvényét!
7. Bizonyítsuk be, hogy ha az
rendszernél határozzuk meg az érkezési
pillanatokban a stacionárius eloszlást, majd ennek felhasználásával
az igények várakozási és tartózkodási idejének
sűrűség- ill. eloszlásfüggvényét!
7. Bizonyítsuk be, hogy ha az 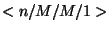 rendszernél
rendszernél 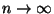 ,
, 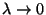 , úgy, hogy
, úgy, hogy 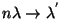 , akkor a rendszerjellemzők az
, akkor a rendszerjellemzők az 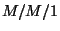 modell megfelelő jellemzőihez tartanak!
modell megfelelő jellemzőihez tartanak!
8. Mutassuk meg, hogy az 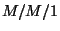 rendszerben
rendszerben 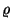 kihasználtságnál és
kihasználtságnál és 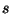 átlagos kiszolgálási időnél a rendszerben való
tartózkodási idő várható értéke mindig kisebb,
mint az
átlagos kiszolgálási időnél a rendszerben való
tartózkodási idő várható értéke mindig kisebb,
mint az 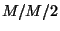 rendszerben
rendszerben 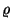 kihasználtsággal és
kihasználtsággal és 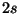 átlagos kiszolgálási idővel!
átlagos kiszolgálási idővel!
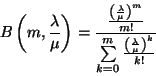
![\begin{displaymath}
C\left(m,{\lambda\over\mu}\right)={\left({{(m\varrho)}^m\ov...
...)}^m\over m!}\right)\left({1\over 1-\varrho}\right)
\right]}
\end{displaymath}](img1036.gif)
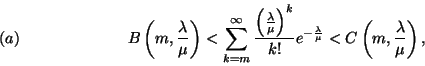
![\begin{displaymath}
C \left(m, {\lambda\over \mu}\right)= { B\left(m, {\lambda\...
...t[1-B \left(m, {\lambda\over \mu}\right)\right]},
\leqno (b)
\end{displaymath}](img1039.gif)
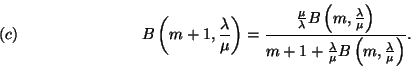
![]() rendszerben
rendszerben ![]() kihasználtságnál és
kihasználtságnál és ![]() átlagos kiszolgálási időnél a rendszerben való
tartózkodási idő várható értéke mindig kisebb,
mint az
átlagos kiszolgálási időnél a rendszerben való
tartózkodási idő várható értéke mindig kisebb,
mint az ![]() rendszerben
rendszerben ![]() kihasználtsággal és
kihasználtsággal és ![]() átlagos kiszolgálási idővel!
átlagos kiszolgálási idővel!