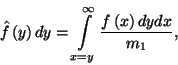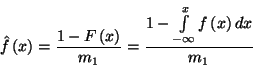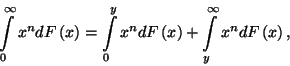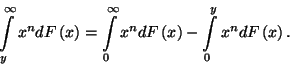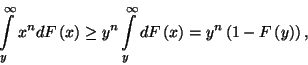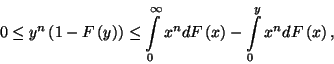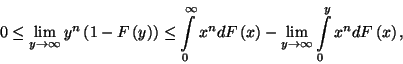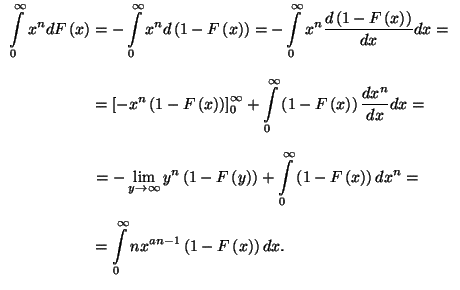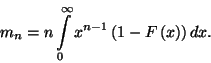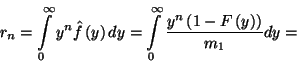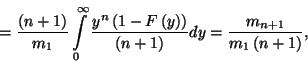III.1.1. A hátralévő élettartam paradoxona
Mielőtt nekilátnánk a beágyazott Markov-láncok ismertetésének,
meg kell értenünk a még hátralévő kiszolgálási
idő néhány tulajdonságát. Azzal az esettel foglalkozunk,
amikor a beérkező igény egy részben kiszolgált igényt
talál a kiszolgáló csatornában. Egy látszólagos
paradoxonnal kezdjük. Tegyük fel, hogy valaki egy tetszőleges pillanatban
egy villamosmegállóhoz ér és aztán villamosra vár.
Tegyük fel még, hogy ehhez a megállóhoz Poisson-folyamat
szerint érkeznek a villamosok, átlagosan percenként 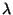 villamos. Átlagosan menny időt kell várnunk a következő
villamos érkezésére? Két, egyaránt logikusnak tűnő
választ is adhatunk:
villamos. Átlagosan menny időt kell várnunk a következő
villamos érkezésére? Két, egyaránt logikusnak tűnő
választ is adhatunk:
Mivel a villamosok beérkezése közötti idő átlagosan
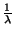 perc, és mivel egy véletlen időpontban érkeztünk,
ezért átlagosan
perc, és mivel egy véletlen időpontban érkeztünk,
ezért átlagosan 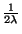 percet kell várnunk.
percet kell várnunk.
A Poisson-folyamat emlékezetnélkülisége miatt a következő
beérkezésig eltelt idő független az előző beérkezés
óta eltelt időtől, tehát átlagosan 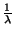 percet kell várnunk. Ezért az utolsó beérkezéstől
addig az időpontig eltelt idő, mikor várni kezdtünk a villamosra,
szintén
percet kell várnunk. Ezért az utolsó beérkezéstől
addig az időpontig eltelt idő, mikor várni kezdtünk a villamosra,
szintén 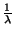 perc. Így az utolsó és a következő
villamos beérkezése közötti idő átlagosan
perc. Így az utolsó és a következő
villamos beérkezése közötti idő átlagosan  perc, ami
perc, ami 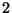 -szer olyan hosszú, mint amilyennek a Poisson folyamat esetében
lennie kellene. Tehát látszólag paradoxonnal állunk szemben.
A következőkben belátjuk, hogy a második válasz a helyes.
Ehhez tetszőleges eloszlású beérkezési időközöket
veszünk, és az egyszerűség kedvéért felújításelméleti
terminológiát használunk, és felújításelméleti
eredményekre is hivatkozunk. Ezekről bővebben olvasható Karlin - Taylor
(1985)-ben. Tekintsük az 1. ábrát.
-szer olyan hosszú, mint amilyennek a Poisson folyamat esetében
lennie kellene. Tehát látszólag paradoxonnal állunk szemben.
A következőkben belátjuk, hogy a második válasz a helyes.
Ehhez tetszőleges eloszlású beérkezési időközöket
veszünk, és az egyszerűség kedvéért felújításelméleti
terminológiát használunk, és felújításelméleti
eredményekre is hivatkozunk. Ezekről bővebben olvasható Karlin - Taylor
(1985)-ben. Tekintsük az 1. ábrát. 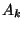 jelentse a
jelentse a 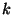 -adik villamost,
-adik villamost, 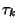 az érkezési időpontját. Tegyük fel, hogy
a
az érkezési időpontját. Tegyük fel, hogy
a 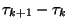 időközök független, azonos eloszlású
valószínűségi változók, melyek eloszlása és
sűrűségfüggvénye:
időközök független, azonos eloszlású
valószínűségi változók, melyek eloszlása és
sűrűségfüggvénye:
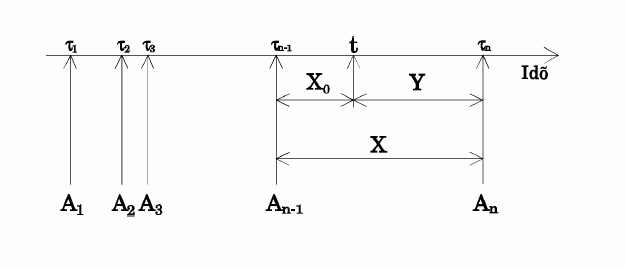
1. ábra
Legyen 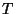 egy elég nagy konstans és a
egy elég nagy konstans és a ![$\left[0,T\right]$](img1061.gif) szakaszon válasszunk ki egy véletlen
szakaszon válasszunk ki egy véletlen 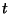 időpontot, ekkor érkezünk a megállóba. Az ábrán
időpontot, ekkor érkezünk a megállóba. Az ábrán
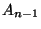 a
a 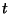 időpont előtt utoljára érkezett villamos, és
időpont előtt utoljára érkezett villamos, és 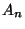 az első amely
az első amely 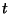 után érkezik. Ezt az
után érkezik. Ezt az 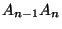 beérkezési időközt jelölje
beérkezési időközt jelölje 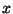 , és legyen
, és legyen 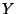 az az idő, amit a következő beérkezésig várnunk
kell. A felújításelmélet nyelvén a
az az idő, amit a következő beérkezésig várnunk
kell. A felújításelmélet nyelvén a 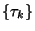 pontok egy felújítási folyamatot alkotnak,
azaz
pontok egy felújítási folyamatot alkotnak,
azaz 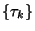 azon felújítási pillanatok sorozata, mikor
egy régi alkatrész tönkremegy és azonnal egy újjal pótolják.
azon felújítási pillanatok sorozata, mikor
egy régi alkatrész tönkremegy és azonnal egy újjal pótolják.
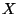 az alkatrész élettartama,
az alkatrész élettartama, 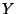 a
a 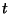 időponthoz képest még hátralévő élettartama,
időponthoz képest még hátralévő élettartama,
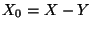 az alkatrész kora. Keressük az
az alkatrész kora. Keressük az 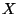 és
és 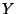 sűrűségfüggvényét. Feltehetjük, hogy a folyamat
régóta tart, mivel csak a határeloszlásokra vagyunk kíváncsiak.
A hátralévő élettartam eloszlását jelölje
sűrűségfüggvényét. Feltehetjük, hogy a folyamat
régóta tart, mivel csak a határeloszlásokra vagyunk kíváncsiak.
A hátralévő élettartam eloszlását jelölje
sűrűségfüggvényét
A kiválasztott 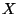 élettartam sűrűségfüggvénye legyen
élettartam sűrűségfüggvénye legyen 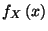 , eloszlásfüggvénye
, eloszlásfüggvénye
Vegyük észre, hogy ha két felújí< tási pont között
hosszú idő telik el, akkor az az időtengely hosszabb szakaszát foglalja
el, mint egy rövidebb időtartam, és nagyobb valószínűséggel
esik a 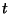 véletlen időpillanat a hosszú intervallumba, mint a rövidbe.
Ennek szellemében el kell fogadnunk azt is, hogy annak a valószínűségnek,
hogy egy
véletlen időpillanat a hosszú intervallumba, mint a rövidbe.
Ennek szellemében el kell fogadnunk azt is, hogy annak a valószínűségnek,
hogy egy 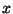 hosszúságú intervallumot választunk ki, arányosnak
kell lennie az
hosszúságú intervallumot választunk ki, arányosnak
kell lennie az 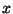 hosszal, és az ilyen hosszúságú intervallumok
relatív gyakoriságával, amit
hosszal, és az ilyen hosszúságú intervallumok
relatív gyakoriságával, amit 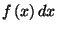 ad meg. Így a kiválasztott intervallumra
felírhatjuk, hogy
ad meg. Így a kiválasztott intervallumra
felírhatjuk, hogy
ahol a bal oldal 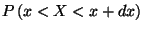 , a jobb oldal pedig tazt jelenti, hogy
ez arányos az intervallum hosszával. A
, a jobb oldal pedig tazt jelenti, hogy
ez arányos az intervallum hosszával. A 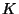 konstanst úgy választjuk, hogy helyesen normalizálja
a sűrűségfüggvényt. Mindkét oldalt integrálva
konstanst úgy választjuk, hogy helyesen normalizálja
a sűrűségfüggvényt. Mindkét oldalt integrálva 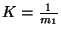 -et kapunk, ahol
-et kapunk, ahol
a felújítások közötti idő várható értéke.
Tehát
Ez azt jelenti, hogy az 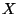 nem
nem 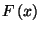 eloszlású! A korábbi példa szavaival
élve ez azt jelenti, hogy az az intervallum, amit azáltal választunk
ki, hogy a villamosmegállóhoz érünk, nem egy tipikus intervallum!
Itt rejlik a paradoxon megoldása: valószínűbb, hogy egy hosszabb
intervallumot fogunk ki, mint egy rövidebbet. Látni fogjuk, hogy Poisson-folyamat
esetében ez azt jelenti, hogy a kiválasztott intervallum kétszer
olyan hosszú, mint egy tipikus intervallum. Keressük most meg a hátralévő
idő
eloszlású! A korábbi példa szavaival
élve ez azt jelenti, hogy az az intervallum, amit azáltal választunk
ki, hogy a villamosmegállóhoz érünk, nem egy tipikus intervallum!
Itt rejlik a paradoxon megoldása: valószínűbb, hogy egy hosszabb
intervallumot fogunk ki, mint egy rövidebbet. Látni fogjuk, hogy Poisson-folyamat
esetében ez azt jelenti, hogy a kiválasztott intervallum kétszer
olyan hosszú, mint egy tipikus intervallum. Keressük most meg a hátralévő
idő 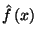 sűrűségfüggvényét. Ha feltesszük,
hogy
sűrűségfüggvényét. Ha feltesszük,
hogy 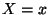 , akkor annak a valószínűsége, hogy az
, akkor annak a valószínűsége, hogy az 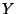 hátralévő élettartam nem haladja meg az
hátralévő élettartam nem haladja meg az 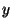 értéket,
értéket,
ha  . Ez azért igaz, mert az
. Ez azért igaz, mert az 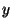 pontot egyenletes eloszlás szerint választottuk. Felírhatjuk
tehát az
pontot egyenletes eloszlás szerint választottuk. Felírhatjuk
tehát az 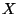 és
és 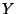 együttes eloszlásfüggvényét:
együttes eloszlásfüggvényét:
ahol  .
. 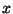 szerint integrálva kapjuk az
szerint integrálva kapjuk az 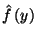 sűrűségfüggvényt, amely
sűrűségfüggvényt, amely 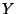 feltétel nélküli sűrűségfüggvénye, azaz
feltétel nélküli sűrűségfüggvénye, azaz
innen
Ez megadja a hátralévő élettartam sűrűségfüggvényét
a beérkezési időközök eloszlásfüggvénye és
várható értéke segítségével. Jelölje 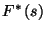 ill.
ill. 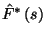 az
az 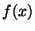 ill.
ill. 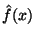 Laplace-transzformáltját. Mivel nemnegatív
valószínűségi változókkal dolgozunk, az
Laplace-transzformáltját. Mivel nemnegatív
valószínűségi változókkal dolgozunk, az 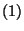 -et egyszerűen transzformálhatjuk a függelékbeli táblázataink
segítségével. Látható, hogy az
-et egyszerűen transzformálhatjuk a függelékbeli táblázataink
segítségével. Látható, hogy az
Laplace-transzformáltja
Ezek után könnyen kifejezhetjük a hátralévő élettartam
momentumait az élettartam momentumaival. Legyen 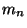 az élettartam
az élettartam 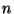 -edik momentuma,
-edik momentuma, 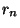 pedig a hátralévő élettartam
pedig a hátralévő élettartam 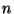 -edik momentuma, azaz
-edik momentuma, azaz 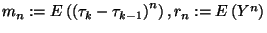 .
Alakítsuk az
.
Alakítsuk az 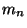 -et.
-et.
így
Mivel
ezért
melyből
azaz
Ezek után parciális integrálással
Tehát
azaz
Speciális esetként kapjuk a várható értéket:
ahol 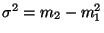 . Emiatt nyilvánvaló, hogy a korábbi
paradoxonra a helyes válasz csak akkor
. Emiatt nyilvánvaló, hogy a korábbi
paradoxonra a helyes válasz csak akkor 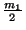 , azaz a beérkezési időköz várható
értékének a fele, ha
, azaz a beérkezési időköz várható
értékének a fele, ha 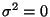 , vagyis állandó beérkezési időközök
esetén. Poisson-típusú beérkezési folyamatnál
, vagyis állandó beérkezési időközök
esetén. Poisson-típusú beérkezési folyamatnál
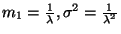 , így
, így 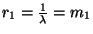 , azaz korábban valóban jó megoldást
adtunk a paradoxonra. Jegyezzük még meg, hogy
, azaz korábban valóban jó megoldást
adtunk a paradoxonra. Jegyezzük még meg, hogy 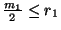 , és
, és 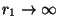 , ha
, ha 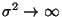 !
!