II.1. Az M/M/1 típusú klasszikus sorbanállási rendszer
Az M/M/1 rendszer a legegyszerűbb nemtriviális rendszer.
Emlékeztetünk rá, hogy ebben az esetben a beérkezési
folyamat
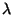
paraméterű Poisson-folyamat, vagyis a beérkezési
idközök
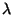
paraméterű exponenciális eloszlású valószínűségi
változók. A kiszolgálási idők
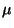
paraméterű exponenciális eloszlású valószínűségi
változók. Feltesszük továbbá, hogy a beérkezési
időközök, és a kiszolgálási idők egymástól
független valószínűségi változók. Jelölje
most
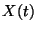
a
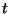
időpillanatban a rendszerben tartózkodó igények számát,
és azt mondjuk, hogy a rendszer a
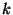
állapotban van, ha
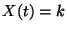
. Mivel a fellépő valószínűségi változók
exponenciális eloszlásúak, vagyis emlékezet nélküliek,
az
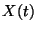
folytonos idejű Markov-lánc lesz. Vizsgáljuk meg a rendszer
állapotváltozásainak valószínűségeit egy adott
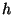
időtartam alatt:
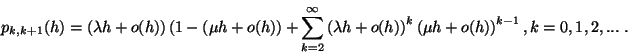
Az összeg első tagja annak a valószínűsége,
hogy a rendszerben egy igény érkezett, és nem szolgáltak
ki egyet sem. Az összeg második tagja pedig annak a valószínűségét
adja, hogy a rendszerbe 2 vagy több igény érkezett, és
a beérkezettnél eggyel kevesebb került kiszolgálásra.
De ez a valószínűség éppen
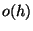
-val egyenlő, így
Az előbbiekhez hasonlóan írható fel annak valószínűsége,
hogy a rendszer
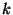
állapotban volt és a
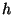
időtartam után a
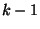
állapotba került:
Könnyen látható továbbá, hogy
Tehát egy olyan születési-halálozási
folyamattal van dolgunk, amit a születési és halálozási
intenzitások alábbi megválasztásával lehet jellemezni:
Vagyis az összes születési intenzitás
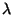
, az összes halálozási intenzitás pedig
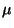
. Feltesszük, hogy végtelen hosszúságú sorok
is létrejöhetnek, és az igények kiszolgálása
FIFO elv alapján történik. Helyettesítsük be az intenzitásokat
a (3)-ba, így a következő adódik:
vagyis
Az eredmény kézenfekvő. Az ergodikusság feltétele
általánosságban (és így annak is, hogy egy
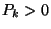
stacionárius megoldást kapjunk)
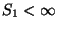
és
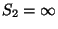
; esetünkben az első feltétel:
Az
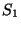
sor akkor és csak akkor konvergens, ha
Az ergodicitás második feltétele esetünkben
Ez akkor teljesül, ha
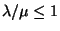
. Tehát az ergodikusság szükséges
és elégséges feltétele az M/M/1 sor esetén egyszerűen
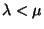
. A
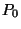
valószínűség kiszámolásához a normalizáló
feltételt használjuk és azt kapjuk, hogy
Mivel
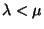
, ezért a sor konvergens, és így
A kihasználtsági tényező
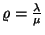
vagy
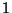
. A stabilitás feltétele miatt a
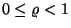
egyenlőséget meg kell követelni. Ez biztosítja,
hogy
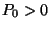
legyen. Így
amely valóban valószínűségi eloszlás,
nevezetesen a geometriai eloszlás. A rendszer
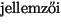
:
(I.) A rendszerben tartózkodó igények átlagos száma:
A rendszerben tartózkodó igények számának
szórásnégyzete:
(II.) A várakozó igények átlagos száma
(átlagos sorhossz):
Az átlagos sorhossz szórásnégyzete:
(III.) A szerver kihasználtsága:
(4) alapján látható, hogy
ahol
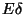
a
kiszolgáló átlagos foglaltsági periódushossza,
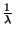
a tétlenségi idő várható értéke.
Mivel a szerver addig tétlen, amíg igény nem érkezik, az
pedig exponenciális eloszlású
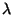
paraméterrel. Így
melyből
(IV.) Egy igény várakozási idejének
eloszlása:
Megmutatjuk, hogy olyan sorbanállási rendszernél, amelybe az
igények Poisson-folyamat szerint érkeznek,
ahol
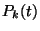
- mint korábban is - annak valószínűsége,
hogy a
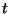
pillanatban a rendszer a
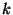
állapotban van,
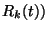
pedig annak valószínűsége, hogy egy a
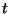
pillanatban érkező igény a rendszert a
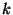
állapotban találja. Jelölje
azt az eseményt, hogy egy beérkezés történik
a
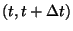
intervallumban. Ekkor
ahol
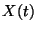
a rendszerbeli igények száma a
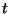
pillanatban. Felhasználva a feltételes valószínűség
definícióját,
Poisson-folyamat esetén tudjuk, hogy (az emlékezetnélküliség
miatt) az
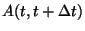
esemény nem függ a
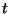
pillanatban a rendszerben tartózkodó igények számától
(és magától a
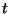
időtől sem), ezért
így
Azaz, annak valószínűsége, hogy egy beérkező
igény a rendszert a
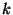
állapotban találja, éppen azzal a valószínűséggel
egyezik meg, hogy a rendszer a
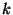
állapotban van. Ha egy tetszőleges pillanatban egy igény
érkezik,
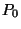
lesz annak a valószínűsége, hogy nem kell várakoznia,
hisz ekkor a rendszer üres. Minden más esetben várakoznia kell.
Tegyük fel, hogy az érkezés pillanatában
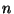
igény tartózkodik a rendszerben. Ekkor az érkező igénynek
meg kell várnia, míg a kiszolgálás alatt álló
igény kiszolgálása befejeződik és az előtte álló
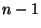
igény elhagyja a rendszert. Feltettük, hogy a kiszolgálások
egymástól függetlenek és
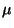
paraméterű exponenciális eloszlásúak. Köztudott,
hogy az exponenciális eloszlás emlékezetnélküli, így
a kiszolgálás alatt levő igény eloszlása független
attól mióta folyik a kiszolgálás, ezért a várakozási
idő
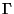
vagy (Erlang-) eloszlású
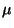
és
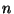
paraméterrel. Emlékeztetőül az
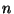
és
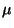
paraméterű Erlang-eloszlás sűrűségfüggvénye:
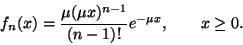
Jelölje
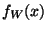
egy tetszőleges igény várakozási idejének
sűrűségfüggvényét,
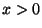
. A teljes valószínűség tétele értelmében:
Tehát
Így
Az átlagos várakozási idő:
(V.) Egy igény tartózkodási idejének
eloszlása:
A gondolatmenet az előzőhöz hasonló, de az igény akkor hagyja
el a rendszert, ha őt is kiszolgálták, így az Erlang eloszlás
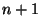 tagból tevődik össze. Tehát a sűrűségfügvény:
tagból tevődik össze. Tehát a sűrűségfügvény:
Az eloszlásfüggvény:
Vagyis azt kaptuk, hogy a tartózkodási idő is exponenciális
eloszlású
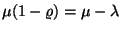
paraméterrel. Ezért az átlagos
rendszerbeli tartózkodási idő:
Továbbá, nyilvánvaló, hogy
Vegyük észre, hogy
Továbbá
A (*) és a (**) összefüggéseket Little-formuláknak
nevezzük, melyek általánosabb esetben is igazak maradnak.
Példa:
1. Egy postahivatalban naponta 70 személy fordul meg (a
posta minden nap 10 óra hosszat van nyitva) ; óránként 10
személyt képesek kiszolgálni. Tételezzük fel, hogy
a beérkezések megfelelnek a Poisson-folyamat jellegzetességeinek
és a kiszolgálás exponenciális eloszlású. Mekkora
lesz a várakozó sor átlagos hossza, mi annak a valószínűsége,
hogy sorban 2-nél több személy várakozzék? Mennyi a
várható sorban állási idő? Mennyi annak a valószínűsége,
hogy a várakozás 20 percnél több időt vesz igénybe?
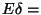
?
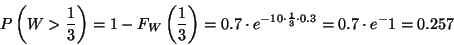
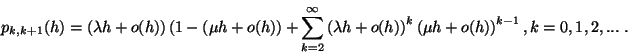
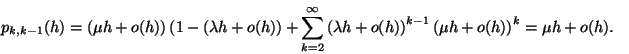
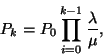
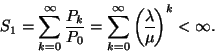
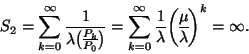
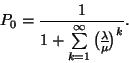
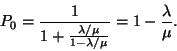
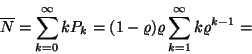

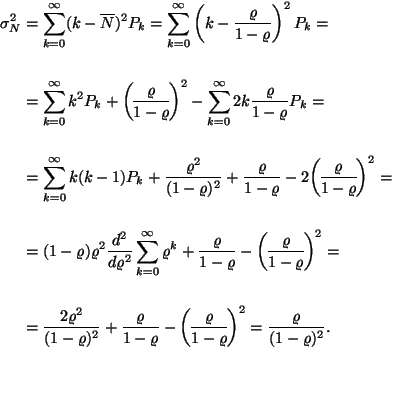
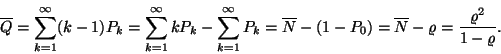
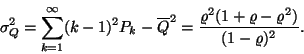
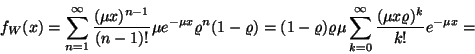
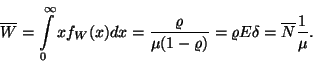
![]() tagból tevődik össze. Tehát a sűrűségfügvény:
tagból tevődik össze. Tehát a sűrűségfügvény:
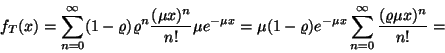
![]()