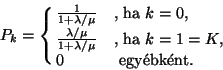II.2. Az M/M/1/K típusú, véges befogadóképességű rendszer
Most olyan sorbanállási rendszereket vizsgálunk, amelyekben rögzített
a várakozó igények számának maximuma. Feltesszük,
hogy a rendszerben legfeljebb 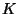 igény tartózkodhat (beleértve a kiszolgáló
egységben levő igényt is), egyetlen ezen felül érkező igény
sem léphet be a rendszerbe, hanem azonnal távozik, anélkül,
hogy kiszolgálnák őt. Továbbra is Poission-folyamat szerint érkeznek
az igények, azonban csak azok az igények léphetnek be a rendszerbe,
amelyek érkezésekor kevesebb, mint
igény tartózkodhat (beleértve a kiszolgáló
egységben levő igényt is), egyetlen ezen felül érkező igény
sem léphet be a rendszerbe, hanem azonnal távozik, anélkül,
hogy kiszolgálnák őt. Továbbra is Poission-folyamat szerint érkeznek
az igények, azonban csak azok az igények léphetnek be a rendszerbe,
amelyek érkezésekor kevesebb, mint 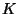 igény van ott. Ennek a látszólag bonyolult rendszernek
a leírását az alábbi módon tudjuk összhangba hozni
a születési-halálozási modellel. Az előzőekhez hasonlóan
nem nehéz belátni, hogy ebben az esetben az alábbi intenzitásokat
kapjuk.
igény van ott. Ennek a látszólag bonyolult rendszernek
a leírását az alábbi módon tudjuk összhangba hozni
a születési-halálozási modellel. Az előzőekhez hasonlóan
nem nehéz belátni, hogy ebben az esetben az alábbi intenzitásokat
kapjuk.
Látszik, hogy ez a rendszer mindig ergodikus, mert állapottere véges.
Továbbá
Természetesen
Szeretnénk kiszámolni a 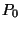 valószínűséget. A normalizáló feltétel
alapján
valószínűséget. A normalizáló feltétel
alapján
végül
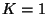 esetén az M/M/1/1 rendszer azt jelenti, hogy egyáltalán
nincs várakozás.
esetén az M/M/1/1 rendszer azt jelenti, hogy egyáltalán
nincs várakozás.
![]() igény tartózkodhat (beleértve a kiszolgáló
egységben levő igényt is), egyetlen ezen felül érkező igény
sem léphet be a rendszerbe, hanem azonnal távozik, anélkül,
hogy kiszolgálnák őt. Továbbra is Poission-folyamat szerint érkeznek
az igények, azonban csak azok az igények léphetnek be a rendszerbe,
amelyek érkezésekor kevesebb, mint
igény tartózkodhat (beleértve a kiszolgáló
egységben levő igényt is), egyetlen ezen felül érkező igény
sem léphet be a rendszerbe, hanem azonnal távozik, anélkül,
hogy kiszolgálnák őt. Továbbra is Poission-folyamat szerint érkeznek
az igények, azonban csak azok az igények léphetnek be a rendszerbe,
amelyek érkezésekor kevesebb, mint ![]() igény van ott. Ennek a látszólag bonyolult rendszernek
a leírását az alábbi módon tudjuk összhangba hozni
a születési-halálozási modellel. Az előzőekhez hasonlóan
nem nehéz belátni, hogy ebben az esetben az alábbi intenzitásokat
kapjuk.
igény van ott. Ennek a látszólag bonyolult rendszernek
a leírását az alábbi módon tudjuk összhangba hozni
a születési-halálozási modellel. Az előzőekhez hasonlóan
nem nehéz belátni, hogy ebben az esetben az alábbi intenzitásokat
kapjuk. 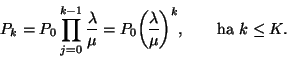
![\begin{displaymath}
P_0=\left[1+\sum_{k=1}^K{\lambda \overwithdelims() \mu }^k\...
...}\right]^{-1}={1-\lambda /\mu \over 1-(\lambda /\mu )^{K+1}},
\end{displaymath}](img546.gif)