II.3. Az M/M/n típusú rendszer

II.3. Az M/M/n típusú rendszer

Ismét olyan $\lambda$ állandó beérkezési intenzitású rendszert vizsgálunk, melyben korlátlan hosszúságú sor kialakulása megengedett. A rendszer db kiszolgálócsatornával (szerverrel) van ellátva. Ez az eset is leírható születési-halálozási folyamattal a következők miatt. Először is tekintsünk független, $\mu_i$ paraméterű exponenciális eloszlású $\xi_i$ valószínűségi változókat. Jelöljük $\eta$ -val ezen $\xi_i$ () változók minimumát. Nem nehéz belátni, hogy $\eta$ is exponenciális eloszlású lesz $\sum\limits_{i=1}^N\mu_i$ paraméterrel. Ugyanis

$\begin{displaymath} P(\eta<x)=1-P(\eta\ge x)=1-P(\xi_i\ge x, \ i=1,...,N)=\end{displaymath}$

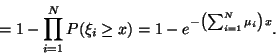
$\begin{displaymath}=1-\prod_{i=1}^N P(\xi_i \ge x)=1-e^{-\left(\sum_{i=1}^N \mu_i\right) x} . \end{displaymath}$

Ezt felhasználva kapjuk meg annak valószínűségét, hogy a rendszer a

idő alatt a

állapotból a

állapotba, ill. a

állapotból a

állapotba kerül. Így

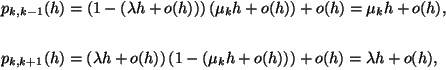
$\begin{displaymath} \eqalign{ p_{k,k-1}(h)=&\left(1-\left(\lambda h+o(h)\right... ...\left(\mu_kh+o(h) \right)\right)+o(h)=\lambda h+o(h),\cr } \end{displaymath}$

ahol

$\begin{displaymath} \mu_k=\min(k\mu , n\mu )=\cases{k\mu &\hbox{, ha $0\leq k\leq n$},\cr n\mu &\hbox{, ha $n< k$}.\cr} \end{displaymath}$

Könnyen látható, hogy az ergodikusság feltétele $\lambda /n\mu <1$ . Amikor hozzákezdünk a

mennyiségek kiszámolásához, azt találjuk, hogy a megoldást két részre kell szétbontanunk, mivel a $\mu_k$ mennyiség kétféle módon függ

-tól. Eszerint, ha

, akkor

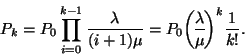
$\begin{displaymath} P_k=P_0\prod_{i=0}^{k-1}{\lambda \over (i+1)\mu }=P_0{\lambda \overwithdelims() \mu }^k{1 \over k!}. \end{displaymath}$

Ha viszont $k\geq n$ , akkor

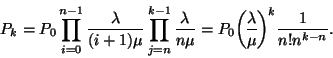
$\begin{displaymath} P_k=P_0\prod_{i=0}^{n-1}{\lambda \over (i+1)\mu }\prod_{j=n... ...u }=P_0{\lambda \overwithdelims() \mu }^k{1 \over n!n^{k-n}}. \end{displaymath}$

Összefoglalva a kapott eredményeket:

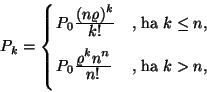
$\begin{displaymath} P_k=\cases{ P_0{\displaystyle(n\varrho )^k \over \displayst... ...kn^n \over \displaystyle n!}&\hbox{, ha $k> n$},\cr & \cr} \end{displaymath}$

ahol

$\begin{displaymath} \varrho ={\lambda \over n\mu }<1. \end{displaymath}$

Ez a $\varrho$ éppen a kihasználtsági tényező. Továbbá

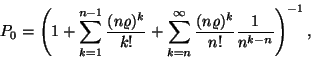
$\begin{displaymath} P_0=\left(1+\sum_{k=1}^{n-1}{(n\varrho )^k \over k!}+\sum_{... ...infty {(n\varrho )^k \over n!}{1 \over n^{k-n}}\right)^{-1}, \end{displaymath}$

és így

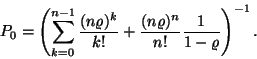
$\begin{displaymath} P_0=\left(\sum_{k=0}^{n-1}{(n\varrho )^k \over k!}+{(n\varrho )^n \over n!}{1 \over 1-\varrho }\right)^{-1}. \end{displaymath}$

Annak a valószínűsége, hogy egy újonnan érkező igénynek sorba kell állnia,

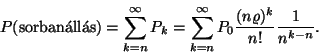
$\begin{displaymath} P(\hbox{sorban\'all\'as})=\sum_{k=n}^\infty P_k=\sum_{k=n}^\infty P_0{(n\varrho )^k \over n!}{1 \over n^{k-n}}. \end{displaymath}$

Ebből

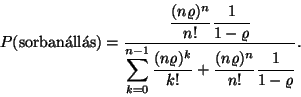
$\begin{displaymath} P(\hbox{sorban\'all\'as})={\displaystyle{(n\varrho )^n \ove... ...)^k \over k!}+{(n\varrho )^n \over n!}{1 \over 1-\varrho }}. \end{displaymath}$

Ezt a valószínűséget széles körben használják a telefonrendszerek vizsgálatával kapcsolatban. Itt annak a valószínűségét adja meg, hogy egy újonnan beérkezett hívás (igény) számára nincs szabad vonal (kiszolgálóegység) egy szerveres rendszerben. Ez az ú.n. Erlang C-formulája, amit többnyire $C(n,\lambda /\mu )$ szimbólummal jelölnek. Az M/M/n rendszer jellemzői:

(I.) Az átlagos sorhossz:

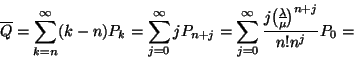
$\begin{displaymath} \overline{Q}=\sum_{k=n}^\infty(k-n)P_k=\sum_{j=0}^\infty jP... ...fty {j{\lambda \overwithdelims() \mu}^{n+j} \over n!n^j}P_0 = \end{displaymath}$

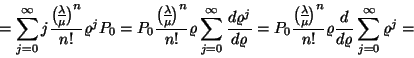
$\begin{displaymath}=\sum_{j=0}^\infty j{{\lambda \overwithdelims() \mu}^n \over ... ...ver n! } \varrho {d \over d\varrho}\sum_{j=0}^\infty\varrho^j=\end{displaymath}$

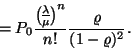
$\begin{displaymath}=P_0{{\lambda \overwithdelims() \mu}^n \over n!}{\varrho \over (1-\varrho)^2}. \end{displaymath}$

(II.) A foglalt szerverek átlagos száma:

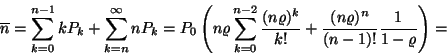
$\begin{displaymath} \overline{n}=\sum_{k=0}^{n-1}kP_k+\sum_{k=n}^\infty nP_k= ... ...r k!}+ {(n\varrho )^n \over(n-1)!}{1 \over 1-\varrho} \right)=\end{displaymath}$

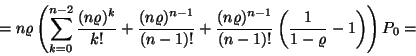
$\begin{displaymath}=n\varrho \left( \sum_{k=0}^{n-2}{(n\varrho )^k\over k!}+ {... ...\over (n-1)!} \left({1 \over 1-\varrho }-1\right) \right)P_0=\end{displaymath}$

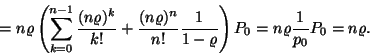
$\begin{displaymath}=n\varrho \left(\sum_{k=0}^{n-1}{(n\varrho )^k \over k!}+ {(... ... 1-\varrho }\right)P_0= n\varrho {1 \over p_0}P_0=n\varrho . \end{displaymath}$

(III.) A rendszerben tartózkodó igények átlagos száma:

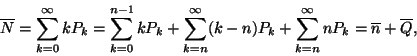
$\begin{displaymath} \overline{N} = \sum_{k=0}^\infty kP_k = \sum_{k=0}^{n-1} kP... ...-n)P_k + \sum_{k=n}^\infty nP_k = \overline{n}+\overline{Q}, \end{displaymath}$

ami egyszerű megfontolásokból is adódik, hiszen egy igény vagy várakozik, vagy kiszolgálás alatt van. A kiszolgálás alatt levők száma viszont megegyezik a foglalt kiszolgálóegységek számával. Ha $\overline{S}$ -gal jelöljük a szabad szerverek vagy kiszolgálóegységek átlagos számát, akkor

$\begin{displaymath} \eqalign{ \overline{n} =&n-\overline{S},\cr \overline{S } =&n-{\lambda \over \mu },\cr } \end{displaymath}$

így

$\begin{displaymath} \overline{N}=n-\overline{S}+\overline{Q}, \end{displaymath}$

vagyis

$\begin{displaymath} \overline{N}-n=\overline{Q}-\overline{S}. \end{displaymath}$

(IV.) A várakozási idő eloszlása:

Egy érkező igénynek akkor kell várakoznia, ha a rendszerben legalább igény tartózkodik. Mivel ebben az esetben a kiszolgálás $n\mu$ paraméterű exponenciális eloszlású valószínűségi változó, az igény várakozási ideje, ha igény tartózkodik a rendszerben Erlang-eloszlású és $n\mu$ paraméterekkel. Így a teljes valószínűség tétele alapján a várakozási idő sűrűségfüggvénye:

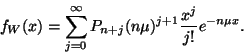
$\begin{displaymath} f_W(x)=\sum_{j=0}^\infty P_{n+j}(n\mu )^{j+1}{x^j \over j!}e^{-n\mu x}. \end{displaymath}$

Behelyettesítve a stacionárius eloszlást

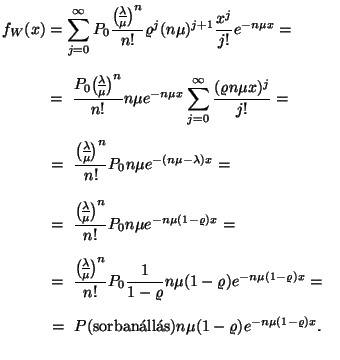
$\begin{displaymath} \eqalign{ f_W(x)= &\sum_{j=0}^\infty P_0{{\lambda \overwit... ...sorban\'all\'as})n\mu (1-\varrho )e^{-n\mu (1-\varrho )x}. } \end{displaymath}$

Vagyis

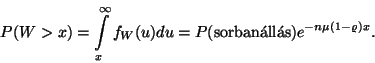
$\begin{displaymath} P(W>x)=\int\limits_x^\infty f_W(u)du=P(\hbox{sorban\'all\'as})e^{-n\mu (1-\varrho )x}. \end{displaymath}$

A várakozási idő eloszlásfüggvénye:

$\begin{displaymath} F_W(x)=1-P(\hbox{sorban\'all\'as})+P(\hbox{sorban\'all\'as})\left(1-e^{-n\mu (1-\varrho )x}\right)=\end{displaymath}$

$\begin{displaymath}=1-P(\hbox{sorban\'all\'as})e^{-n\mu (1-\varrho )x}. \end{displaymath}$

Innen az átlagos várakozási idő:

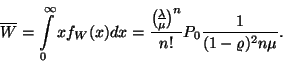
$\begin{displaymath} \overline{W}=\int\limits_0^\infty xf_W(x)dx={{\lambda \over... ...delims() \mu }^n \over n!}P_0{1 \over (1-\varrho )^2n\mu }. \end{displaymath}$

(V.) A tartózkodási idő eloszlása:

A kiszolgálás azonnal elkezdődik, ha a rendszerben -nél kevesebb igény tartózkodik, így stacionárius esetben egy érkező igény rendszerben eltöltött ideje megegyezik a kiszolgálási idővel. Azonban, ha várakoznia kell, akkor a várakozási idő és a kiszolgálási idő összege, vagyis az eloszlás két független eloszlás összege, mely közül az egyik $\mu$ paraméterű exponenciális, a másik pedig a rendszertől függő paraméterű Erlang-eloszlás. A tartózkodási idő sűrűségfüggvényét a következő módon határozzuk meg.

$\begin{displaymath} f_T(x)=P(\hbox{nincs sorban\'all\'as})\mu e^{-\mu x} +f_{W+S}(x) \end{displaymath}$

Tudjuk, hogy

$\begin{displaymath} f_W(x)=P(\hbox{sorban\'all\'as})e^{-n\mu (1-\varrho )x}n\mu (1-\varrho ). \end{displaymath}$

Ekkor

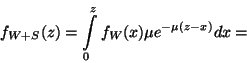
$\begin{displaymath} f_{W+S}(z)=\int\limits_0^zf_W(x)\mu e^{-\mu (z-x)}dx=\end{displaymath}$

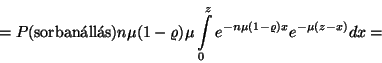
$\begin{displaymath}=P(\hbox{sorban\'all\'as})n\mu (1-\varrho )\mu \int\limits_0^ze^{-n\mu (1-\varrho )x}e^ {-\mu (z-x)}dx=\end{displaymath}$

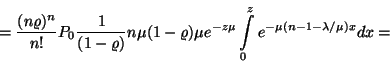
$\begin{displaymath}={(n\varrho )^n \over n!}P_0{1 \over (1-\varrho )}n\mu (1-\va... ... \mu e^{-z\mu }\int\limits_0^ze^{-\mu (n-1-\lambda /\mu )x}dx=\end{displaymath}$

$\begin{displaymath} ={(n\varrho )^n \over n!}P_0n\mu {1 \over n-1-\lambda /\mu }e^{-\mu z} \left(1-e^{-\mu (n-1-\lambda /\mu )z}\right). \end{displaymath}$

Ezért

$\begin{displaymath} f_T(x) =\left(1-{\lambda \overwithdelims() \mu }^n{P_0 \over n!(1-\varrho )} \right)\mu e^{-\mu x}+\end{displaymath}$

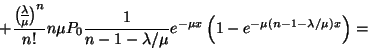
$\begin{displaymath}+{{\lambda \overwithdelims() \mu }^n \over n!}n\mu P_0{1 \ov... .../\mu } e^{-\mu x}\left(1-e^{-\mu (n-1-\lambda /\mu )x}\right)=\end{displaymath}$

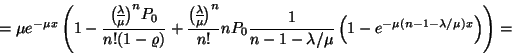
$\begin{displaymath}=\mu e^{-\mu x}\left(1-{{\lambda \overwithdelims() \mu }^nP_0... ...mbda /\mu }\left(1-e^{-\mu (n-1-\lambda /\mu )x}\right)\right)=\end{displaymath}$

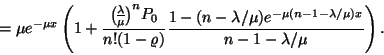
$\begin{displaymath}=\mu e^{-\mu x}\left(1+{{\lambda \overwithdelims() \mu }^nP_0... ...)e^{-\mu (n-1-\lambda /\mu )x}\over n-1-\lambda /\mu }\right). \end{displaymath}$

Így

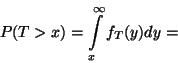
$\begin{displaymath} P(T>x)=\int\limits_x^\infty f_T(y)dy=\end{displaymath}$

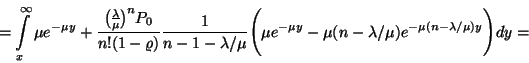
$\begin{displaymath}=\int\limits_x^\infty \mu e^{-\mu y}+ {{\lambda \overwithde... ...y}-\mu (n-\lambda /\mu ) e^{-\mu (n-\lambda /\mu)y}\Biggr)dy=\end{displaymath}$

$\begin{displaymath}=e^{-\mu x}+{\lambda \overwithdelims() \mu }^nP_0 {1 \over ... ...a /\mu)} \left(e^{-\mu x}-e^{-\mu (n-\lambda /\mu )x}\right)=\end{displaymath}$

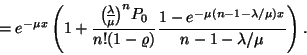
$\begin{displaymath}=e^{-\mu x} \left( 1+{{\lambda \overwithdelims() \mu }^nP... ...^{-\mu (n-1-\lambda /\mu)x} \over n-1-\lambda /\mu} \right). \end{displaymath}$

Innen

$\begin{displaymath} F_T(x)=1-P(T>x). \end{displaymath}$

Továbbá

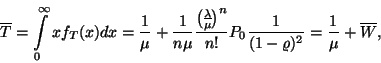
$\begin{displaymath} \eqalign{ \overline{T}=&\int\limits_0^\infty xf_T(x)dx =... ..._0{1 \over (1-\varrho)^2} ={1 \over \mu }+\overline{W}, } \end{displaymath}$

mint az várható volt.

Stacionárius esetben a távozó igények átlagos számának meg kell egyeznie az érkező igények átlagos számával, így a rendszerben tartózkodók átlagos száma állandó. Tehát annyi igény tartózkodik átlagosan a rendszerben, amennyi érkezik egy igény tartózkodási ideje alatt, vagyis

$\begin{displaymath} \lambda\overline{T}=\overline{N}=\overline{Q}+\overline{n}, \end{displaymath}$

továbbá

$\begin{displaymath} \lambda\overline{W}=\overline{Q}. \end{displaymath}$

Ezek az ún. Little-formulák, melyeket számolás útján is könnyen bizonyíthatunk. Ugyanis, mint beláttuk

$\begin{displaymath} \overline{N}=n\varrho +P_0{(n\varrho )^n \over n!(1-\varrho )^2}\varrho. \end{displaymath}$

Mivel

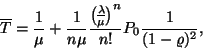
$\begin{displaymath} \overline{T}={1 \over \mu}+{1 \over n\mu } {{\lambda \overwithdelims() \mu }^n \over n!} P_0{1 \over (1-\varrho )^2}, \end{displaymath}$

így

$\begin{displaymath} \lambda\overline{T}={\lambda \over \mu }+ {(n\varrho)^n \over n!} P_0{\varrho \over (1-\varrho )^2}, \end{displaymath}$

vagyis

$\begin{displaymath} \overline{N}=\lambda\overline{T}, \end{displaymath}$

mivel ${\lambda\over\mu} = n\varrho$ . Továbbá

$\begin{displaymath} \overline{Q}=\lambda \overline{W}, \end{displaymath}$

mivel

$\begin{displaymath} \overline{n}=n\varrho. \end{displaymath}$

(VI.) A szerverek összkihasználtsága:

Egy szerver kihasználtsága nyilvánvalóan

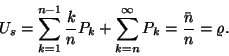
$\begin{displaymath} U_s=\sum\limits_{k=1}^{n-1}{k\over n}P_k+\sum\limits_{k=n}^\infty P_k={\bar{n} \over n}=\varrho. \end{displaymath}$

Így az összkihasználtság

$\begin{displaymath} U_n=nU_s=\bar{n}. \end{displaymath}$

(VII.) A foglaltsági periódushosszak:

A rendszert akkor nevezzük tétlennek, ha a rendszerben nem tartózkodik igény, minden más esetben foglaltnak nevezzük. Jelölje a $E\delta^{(n)}$ a rendszer átlagos foglaltsági periódushosszát. Ekkor (4) miatt a rendszer kihasználtsága

$\begin{displaymath} U_r=1-P_0={E\delta^{(n)} \over {1 \over \lambda }+E\delta^{(n)}}, \end{displaymath}$

melyből

$\begin{displaymath} E\delta^{(n)}={1-P_0 \over \lambda P_0}. \end{displaymath}$

Ha az egyes kiszolgáló egységeket tekintjük és feltesszük, hogy üres egységnél, szervernél ahhoz érkezik hamarabb igény, amely korábban vált üressé, akkor ha

igény tartózkodik a rendszerben, a szabad szerverek száma

. Tekintsünk egy konkrét szervert és tegyük fel, hogy a rendszerben

igény tartózkodik a szerver szabaddá válása pillanatában. Ekkor ezen szerver átlagos üresjárati ideje ilyen feltételek mellett

$\begin{displaymath} \overline{e}_j={n-j \over \lambda}. \end{displaymath}$

Annak a valószínűsége, hogy ebben az állapotban van

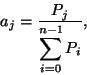
$\begin{displaymath} a_j={P_j \over \displaystyle\sum_{i=0}^{n-1} P_i}, \end{displaymath}$

így egy szerver átlagos szabad periódushossza:

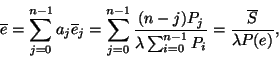
$\begin{displaymath} \overline{e}=\sum_{j=0}^{n-1}a_j\overline{e}_j =\sum_{j=0... ...da \sum_{i=0}^{n-1}P_i} ={\overline{S} \over \lambda P(e)}, \end{displaymath}$

ahol

annak a stacionárius valószínűsége, hogy egy érkező igénynek nem kell várakoznia. Ekkor ismét (4) szerint

$\begin{displaymath} U_s=\varrho ={E\delta \over \overline{e}+E\delta}, \end{displaymath}$

melyből

$\begin{displaymath} \varrho\overline{e}=(1-\varrho)E\delta , \end{displaymath}$

ahol $\varrho$ annak stacionárius valószínűsége, ho=gy a szerver nem üres, $E\delta$ pedig az átlagos foglaltsági periódushossza. Így

$\begin{displaymath} E\delta ={\varrho \over 1-\varrho}{\overline{S} \over \lambda P(e)}. \end{displaymath}$

esetben

$\begin{displaymath} \overline{S}=1-\varrho, \qquad P(e)=P_0=1-\varrho, \qquad \varrho={\lambda \over \mu}, \end{displaymath}$

így

$\begin{displaymath} E\delta={1 \over \mu -\lambda}, \end{displaymath}$

mely a jól ismert képlet. ${\bold P\'elda:}$

Adott egy 4 csatornás telefonközpont, $\lambda=6$ , $\mu=2$ intenzitásokkal. Határozzuk meg a rendszer jellemzőit!

${\bold Megold\'as:}$

$\begin{displaymath}P_0=0.0377,\ \ \overline{Q}=1.528,\ \ \overline{N}=4.528,\ \ \overline{S}=1, \ \ \overline{n}=3\end{displaymath}$

$\begin{displaymath}P(W>0)=C(4,3)=0.509\end{displaymath}$

$\overline{W}=0.255$ időegység, $\overline{T}=0.755$ időegység, $U_s={3\over 4}$ , $\overline{e}=0.35$ időegység, $E\delta =1.05$ időegység, $E\delta^{(4)}=4.2$ időegység, .

Nyitólap Tartalomjegyzék Fejezetek ( B I II III IV F ) Letöltések

FRAME-mel

FRAME nélkül

<< Előző

Következő >>