II.4. Az M/M/n/n típusú Erlang-féle veszteséges rendszer
Ezen modellre 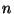 csatornás veszteséges rendszerként is szokás hivatkozni
az alábbiak miatt. Az
csatornás veszteséges rendszerként is szokás hivatkozni
az alábbiak miatt. Az 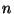 csatornás rendszerbe Poisson-folyamat szerint érkeznek az
igények. Ha van üres csatorna vagy szerver az igény kiszolgálása
exponenciális időtartamú
csatornás rendszerbe Poisson-folyamat szerint érkeznek az
igények. Ha van üres csatorna vagy szerver az igény kiszolgálása
exponenciális időtartamú 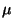 paraméterrel. Ha minden kiszolgáló egység foglalt,
akkor az igény elvész, azaz sorbanállás nem megengedett. Ezen
probléma a tömegkiszolgálás egyik legrégibb problémája,
mellyel a század elején a telefonközpontok kihasználtságával
kapcsolatban foglalkozott A. K. Erlang és C. Palm. Hasonló jelenséggel
találkozunk a parkolóhelyek esetében is. A feltételek alapján
ez is egy születési-kihalási folyamattal modellezhető, melynek
intenzitásai a következők:
paraméterrel. Ha minden kiszolgáló egység foglalt,
akkor az igény elvész, azaz sorbanállás nem megengedett. Ezen
probléma a tömegkiszolgálás egyik legrégibb problémája,
mellyel a század elején a telefonközpontok kihasználtságával
kapcsolatban foglalkozott A. K. Erlang és C. Palm. Hasonló jelenséggel
találkozunk a parkolóhelyek esetében is. A feltételek alapján
ez is egy születési-kihalási folyamattal modellezhető, melynek
intenzitásai a következők:
Azt mondjuk, hogy a folyamat 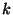 állapotban van, ha
állapotban van, ha 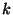 szerver foglalt, azaz ha
szerver foglalt, azaz ha 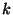 igény tartózkodik a rendszerben. Nyilvánvalóan
az e rgodikus eloszlás létezik, mivel a folyamat véges állapotterű.
A folyamat stacionárius eloszlása:
igény tartózkodik a rendszerben. Nyilvánvalóan
az e rgodikus eloszlás létezik, mivel a folyamat véges állapotterű.
A folyamat stacionárius eloszlása:
A normalizáló feltétel miatt:
így
A rendszer egyik jellemzője a
valószínűség, melyet először Erlang vezetett be (1917-ben)
és Erlang-féle veszteségformula vagy Erlang-féle B formula
néven ismert, általában 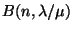 szimbólummal jelölik. A
szimbólummal jelölik. A 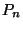 valószínűség annak a valószínűsége
stacionárius esetben, hogy egy újonnan érkező igényt nem fogad
a rendszer, azaz az igény elveszik.
valószínűség annak a valószínűsége
stacionárius esetben, hogy egy újonnan érkező igényt nem fogad
a rendszer, azaz az igény elveszik.
Kis 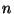 -re a
-re a 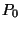 valószínűség könnyen kiszámolható.
Nagy
valószínűség könnyen kiszámolható.
Nagy 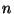 -re és kis
-re és kis 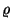 -ra
-ra 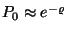 , így
, így
azaz a Poisson-eloszlás. Nagy 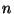 -re és nagy
-re és nagy 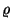 -ra általában
-ra általában
Ebben az esetben a nevező a 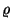 közepű Poisson-eloszlás első
közepű Poisson-eloszlás első 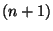 tagjának összege. Elegendő nagy
tagjának összege. Elegendő nagy 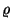 -ra (
-ra (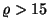 ) a Poissson-eloszlást közelítjük
) a Poissson-eloszlást közelítjük
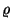 közepű és
közepű és 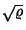 szórású normális eloszlással,
így
szórású normális eloszlással,
így
ahol
és
Az M/M/n/n rendszer jellemzői:
(I.) A rendszerben tartózkodó igények átlagos száma,
a foglalt szerverek átlagos száma:
így 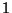 szerverre jutó átlagos igényszám:
szerverre jutó átlagos igényszám:
(II.) A szerverek kihasználtsága:
Mint már láttuk
Jelen esetben
(III.) Az átlagos tétlenségi idő (egy konkrét kiszolgáló
esetén): A jól ismert (4) vagy (5) összefüggést alkalmazva:
ahol 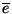 az átlagos tétlenségi idő. Így
az átlagos tétlenségi idő. Így
tehát
Ha az üres szerverek olyan sorrendben kezdik kiszolgálni az érkező
igényeket, mint amilyen sorrendben megüresedtek, akkor egy szerver működését
a következőképpen írhatjuk le. Ha egy üressé vált
szerver 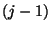 másik üres szervert talál megüresedése
pillanatában, akkor csak a
másik üres szervert talál megüresedése
pillanatában, akkor csak a 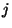 -edik igény kiszolgálásával kezdődik ismét
a foglaltsági periódusa. Jelölje
-edik igény kiszolgálásával kezdődik ismét
a foglaltsági periódusa. Jelölje 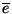 a szerver átlagos üresjárati periódusa
hosszát,
a szerver átlagos üresjárati periódusa
hosszát, 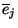 pedig a fenti állapotban az átlagos tétlenségi
időt. Nyilvánvalóan
pedig a fenti állapotban az átlagos tétlenségi
időt. Nyilvánvalóan 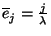 ,
, 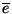 pedig a teljes várható érték tétele
alapján:
pedig a teljes várható érték tétele
alapján:
azaz más úton is ugyanarra az eredményre jutunk.
(IV.) A rendszer átlagos foglaltsági periódushosszap:
Nyilvánvalóan (4) alapján
melyből
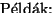 1. Egy parkolóhoz az autók
1. Egy parkolóhoz az autók 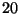 másodpercenként érkeznek, és átlagosan
másodpercenként érkeznek, és átlagosan 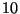 percig maradnak. A beérkezés Poisson, a kiszolgálás
exponenciális. Milyen nagynak kell lennie a parkolónak, hogy egy autó
legfeljebb 1% eséllyel forduljon vissza, mert a parkoló telített?
percig maradnak. A beérkezés Poisson, a kiszolgálás
exponenciális. Milyen nagynak kell lennie a parkolónak, hogy egy autó
legfeljebb 1% eséllyel forduljon vissza, mert a parkoló telített?
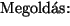
a normális eloszlású közelítést követve
Ebből
A normális eloszlás táblázatából nem nehéz
ellenőrizni, hogy 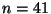 .
2. Egy
.
2. Egy 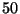 csatornás telefonközpontba átlagosan
csatornás telefonközpontba átlagosan 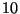 percenként érkeznek hívások Poisson-eloszlás
szerint. A kiszolgálási idő exponenciális,
percenként érkeznek hívások Poisson-eloszlás
szerint. A kiszolgálási idő exponenciális, 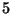 perc átlaggal. Határozzuk meg a rendszer jellemzőit!
perc átlaggal. Határozzuk meg a rendszer jellemzőit!
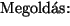 Esetünkben Poisson eloszlással való
közelítés használható,
Esetünkben Poisson eloszlással való
közelítés használható, 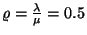 értékkel.
értékkel. 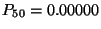 a Poisson-eloszlás szerint, sőt, még
a Poisson-eloszlás szerint, sőt, még 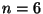 -nál is
-nál is 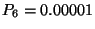 . Ez azt jelenti, hogy igény szinte sohasem lesz elutasítva.
A foglalt csatornák átlagos száma:
. Ez azt jelenti, hogy igény szinte sohasem lesz elutasítva.
A foglalt csatornák átlagos száma:
így az egy csatornára jutó átlagos igényszám:
mely egyben a csatornák kihasználtsága. 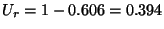 , mely a rendszer kihasználatsága. A rendszer
átlagos foglaltsági periódushossza:
, mely a rendszer kihasználatsága. A rendszer
átlagos foglaltsági periódushossza:
A csatornák átlagos tétlenségi ideje:
![]() csatornás veszteséges rendszerként is szokás hivatkozni
az alábbiak miatt. Az
csatornás veszteséges rendszerként is szokás hivatkozni
az alábbiak miatt. Az ![]() csatornás rendszerbe Poisson-folyamat szerint érkeznek az
igények. Ha van üres csatorna vagy szerver az igény kiszolgálása
exponenciális időtartamú
csatornás rendszerbe Poisson-folyamat szerint érkeznek az
igények. Ha van üres csatorna vagy szerver az igény kiszolgálása
exponenciális időtartamú ![]() paraméterrel. Ha minden kiszolgáló egység foglalt,
akkor az igény elvész, azaz sorbanállás nem megengedett. Ezen
probléma a tömegkiszolgálás egyik legrégibb problémája,
mellyel a század elején a telefonközpontok kihasználtságával
kapcsolatban foglalkozott A. K. Erlang és C. Palm. Hasonló jelenséggel
találkozunk a parkolóhelyek esetében is. A feltételek alapján
ez is egy születési-kihalási folyamattal modellezhető, melynek
intenzitásai a következők:
paraméterrel. Ha minden kiszolgáló egység foglalt,
akkor az igény elvész, azaz sorbanállás nem megengedett. Ezen
probléma a tömegkiszolgálás egyik legrégibb problémája,
mellyel a század elején a telefonközpontok kihasználtságával
kapcsolatban foglalkozott A. K. Erlang és C. Palm. Hasonló jelenséggel
találkozunk a parkolóhelyek esetében is. A feltételek alapján
ez is egy születési-kihalási folyamattal modellezhető, melynek
intenzitásai a következők: 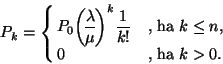
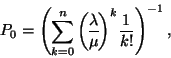
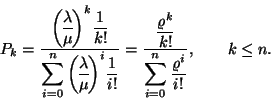
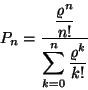
![]() -re a
-re a ![]() valószínűség könnyen kiszámolható.
Nagy
valószínűség könnyen kiszámolható.
Nagy ![]() -re és kis
-re és kis ![]() -ra
-ra ![]() , így
, így 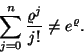
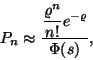
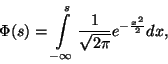
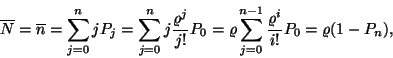
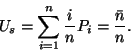
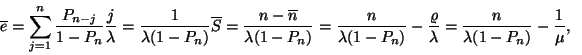
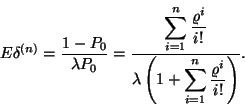
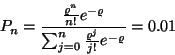
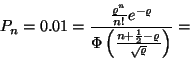
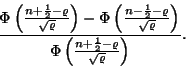
![]()