I.1. Felújításelmélet
Legyenek 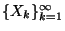 nemnegatív, azonos eloszlású, egymástól
független valószínűségi változók. Az
nemnegatív, azonos eloszlású, egymástól
független valószínűségi változók. Az
valószínűségi változók segítségével definiáljuk
a következő folyamatot
1. Definíció Az 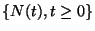 sztochasztikus folyamatot felújítási
folyamatnak nevezzük.
A következő interpretációt adhatjuk. Bizonyos események bekövetkezését
figyeljük. Jelölje
sztochasztikus folyamatot felújítási
folyamatnak nevezzük.
A következő interpretációt adhatjuk. Bizonyos események bekövetkezését
figyeljük. Jelölje 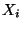 az
az 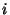 -edik és az
-edik és az 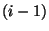 -edik esemény közötti időtartamot. Ekkor
-edik esemény közötti időtartamot. Ekkor 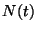 a
a 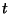 időtartam alatt bekövetkezett események számát
adja. Az
időtartam alatt bekövetkezett események számát
adja. Az 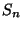 valószínűségi változót az
valószínűségi változót az 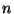 -edik esemény bekövetkezéséhez szükséges
várakozási időnek nevezzük. Könnyű belátni, hogy
-edik esemény bekövetkezéséhez szükséges
várakozási időnek nevezzük. Könnyű belátni, hogy
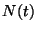 realizációi jobbról folytonos lépcsős függvények,
ahol egységnyi ugrások történnek az
realizációi jobbról folytonos lépcsős függvények,
ahol egységnyi ugrások történnek az 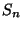 időpillanatokban. Az
időpillanatokban. Az 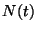 definíciójából egyből következik, hogy
definíciójából egyből következik, hogy
( 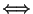 az ekvivalenciát jelöli) Vezessük
be a következő jelöléseket. Legyen
az ekvivalenciát jelöli) Vezessük
be a következő jelöléseket. Legyen
ahol
vagyis 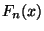 az
az 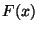 eloszlásfüggvény önmagával vett
eloszlásfüggvény önmagával vett 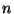 -szeres konvolúciója. (Jelölése
-szeres konvolúciója. (Jelölése 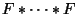 .) Feltehetjük, hogy
.) Feltehetjük, hogy 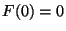 .
2. Definíció Az
.
2. Definíció Az 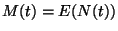 függvényt felújítási függvénynek
nevezzük.
Az alábbiakban
függvényt felújítási függvénynek
nevezzük.
Az alábbiakban 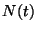 -re és
-re és 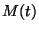 -re mondunk ki néhány fontos tételt.
1. Tétel
-re mondunk ki néhány fontos tételt.
1. Tétel
Bizonyítás. Látható, hogy
vagyis
Azonban így
Továbbá
Meg lehet mutatni, hogy
Meg kell jegyeznünk, hogy ha 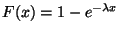 , akkor
, akkor 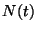
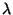 paraméterű Poisson-folyamatot alkot.
2. Tétel Az
paraméterű Poisson-folyamatot alkot.
2. Tétel Az 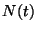 folyamatra teljesül a nagy számok erős törvénye,
azaz
folyamatra teljesül a nagy számok erős törvénye,
azaz 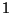 valószínűséggel
valószínűséggel
ahol 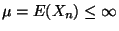 .
Bizonyítás. Tekintsük a
.
Bizonyítás. Tekintsük a ![$(0,t]$](img47.gif) intervallumot, ekkor
intervallumot, ekkor
Azonban az 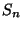 sorozatra igaz a nagy számok erős törvénye, azaz
sorozatra igaz a nagy számok erős törvénye, azaz
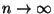 esetén
esetén
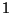 valószínűséggel. Továbbá
valószínűséggel. Továbbá 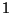 valószínűséggel
valószínűséggel
Hasonlóan, 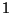 valószínűséggel
valószínűséggel
Így az
relációból az
összefüggést kapjuk.
Az alábbiakban bizonyítás nélkül közlünk
néhány fontos tételt, amelyek az alkalmazásban nagy szerepet
játszanak.
3. Tétel(Elemi felújítási
tétel)
4. Tétel
ahol 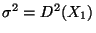 .
5. Tétel Legyen
.
5. Tétel Legyen 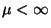 , és
, és 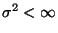 . Ekkor
. Ekkor
3. Definíció Az 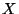 nemnegatív valószínűségi változót (vagy
az
nemnegatív valószínűségi változót (vagy
az 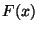 eloszlásfüggvényt) rácsosnak nevezzük,
ha létezik olyan
eloszlásfüggvényt) rácsosnak nevezzük,
ha létezik olyan 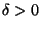 , melyre
, melyre 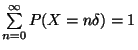 , azaz
, azaz 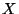 értékei
értékei 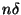 alakú számok. Ekkor
alakú számok. Ekkor 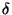 -t
-t 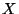 periódusának nevezzük.
6. Tétel (Blackwell-tétel) (i) Ha
periódusának nevezzük.
6. Tétel (Blackwell-tétel) (i) Ha 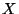 nem rácsos eloszlású, akkor
nem rácsos eloszlású, akkor 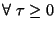 esetén
esetén
(ii) Ha 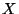 periódusa
periódusa 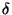 , akkor
, akkor
Legyen 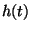 korlátos függvény a
korlátos függvény a 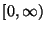 -en. Továbbá tegyük fel, hogy az alábbi
feltételek is teljesülnek még
(i)
-en. Továbbá tegyük fel, hogy az alábbi
feltételek is teljesülnek még
(i) 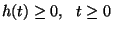 ,
(ii)
,
(ii) 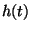 nemnövekvő,
(iii)
nemnövekvő,
(iii) 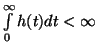 . Ekkor kimondhatjuk az
ún. alaptételt, amely nagyon nagy jelentőségű az alkalmazott valószínűségszámítási
modelleknél.
7. Tétel (Smith-tétel, vagy a felújításelmélet
alaptétele) Ha
. Ekkor kimondhatjuk az
ún. alaptételt, amely nagyon nagy jelentőségű az alkalmazott valószínűségszámítási
modelleknél.
7. Tétel (Smith-tétel, vagy a felújításelmélet
alaptétele) Ha 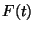 nem rácsos, akkor
nem rácsos, akkor
Meg kell jegyeznünk, hogy a Blackwell-tétel és Smith-tétel
ekvivalensek. Térjünk vissza az
összefüggésre. Látható, hogy
Az
összefüggést felújítási egyenletnek nevezzük.
Az
Laplace-Stieltjes transzformáltakra igaz
Ebből
illetve
azaz 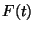 és
és 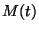 kölcsönösen meghatározzák egymást.
Először általánosítjuk a felújítási
egyenletet a következőképpen:
kölcsönösen meghatározzák egymást.
Először általánosítjuk a felújítási
egyenletet a következőképpen:
ahol 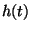 és
és 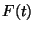 ismert függvények
ismert függvények 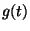 pedig az ismeretlen a fenti integrálegyenletben. Megmutatjuk,
hogy
pedig az ismeretlen a fenti integrálegyenletben. Megmutatjuk,
hogy
ahol 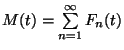 a felújítási függvény.
Vegyük a Laplace-Stieltjes transzformáltakat mindkét oldalon. Ekkor
a felújítási függvény.
Vegyük a Laplace-Stieltjes transzformáltakat mindkét oldalon. Ekkor
Ebből az előzőek szerint
Invertálva
Vezessük be a következő valószínűségi változókat:
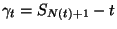 : hátralévő élettartam,
: hátralévő élettartam, 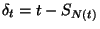 : eltelt időtartam, vagy életkor,
: eltelt időtartam, vagy életkor, 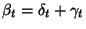 : teljes élettartam. Vizsgáljuk
mo<st meg a
: teljes élettartam. Vizsgáljuk
mo<st meg a 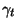 hátralévő élettartam és a
hátralévő élettartam és a 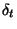 eltelt időtartam asszimptotikus eloszlását! A definíciókból
látható, hogy
eltelt időtartam asszimptotikus eloszlását! A definíciókból
látható, hogy
Így
amely az általánosított felújítási egyenlet. Legyen
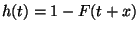 . Mint láttuk
. Mint láttuk
Tekintsük a 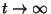 határátmenetet. Vegyük észre, hogy
határátmenetet. Vegyük észre, hogy 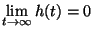 , és alkalmazva a Smith-féle
alaptételt
, és alkalmazva a Smith-féle
alaptételt
A 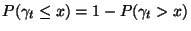 alapján
alapján
illetve
ha 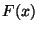 nem rácsos.
Tekintsük a
nem rácsos.
Tekintsük a 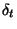 ,
, 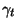 valószínűségi változókat. Vegyük
észre, hogy
valószínűségi változókat. Vegyük
észre, hogy
és
Ebből
Az előzőek alapján
Bebizonyítható, hogy
Az is belátható, hogy
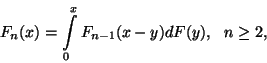
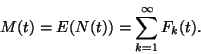
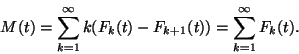
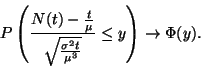
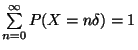 , azaz
, azaz 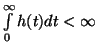 . Ekkor kimondhatjuk az
ún. alaptételt, amely nagyon nagy jelentőségű az alkalmazott valószínűségszámítási
modelleknél.
7. Tétel (Smith-tétel, vagy a felújításelmélet
alaptétele) Ha
. Ekkor kimondhatjuk az
ún. alaptételt, amely nagyon nagy jelentőségű az alkalmazott valószínűségszámítási
modelleknél.
7. Tétel (Smith-tétel, vagy a felújításelmélet
alaptétele) Ha 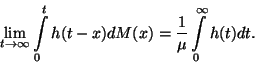
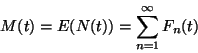
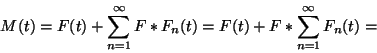
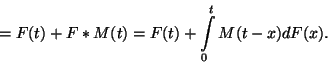
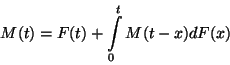
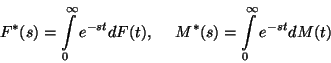
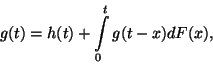
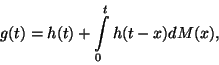
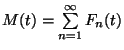 a felújítási függvény.
Vegyük a Laplace-Stieltjes transzformáltakat mindkét oldalon. Ekkor
a felújítási függvény.
Vegyük a Laplace-Stieltjes transzformáltakat mindkét oldalon. Ekkor
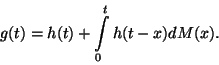
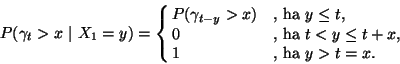
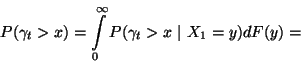
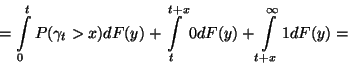
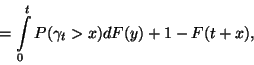
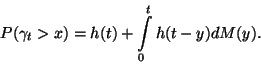
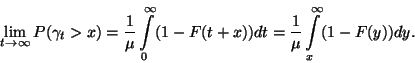
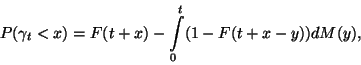
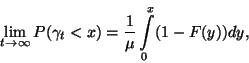
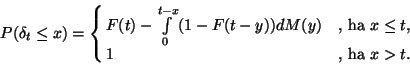
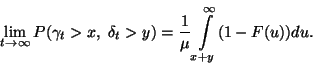
![]()