![]()
Tekintsünk egy homogén Markov-láncot
![]()
átmenetvalószínűségekkel. Legyen továbbá ![]() . Nyilvánvalóan fennáll, hogy
. Nyilvánvalóan fennáll, hogy ![]() és
és ![]() . A
. A ![]() átmenetvalószínűségek elrendezhetők a következő
mátrix alakban:
átmenetvalószínűségek elrendezhetők a következő
mátrix alakban:
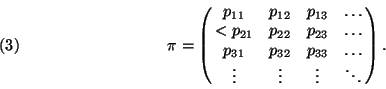
![]() az ún. átmenetvalószínűségek mátrixa.
A
az ún. átmenetvalószínűségek mátrixa.
A ![]() mátrix négyzetes, elemei nem negatívak, és a
sorok összege
mátrix négyzetes, elemei nem negatívak, és a
sorok összege ![]() . Egy ilyen mátrixot sztochasztikus mátrixnak nevezünk.
Egy Markov-lánc egyértelműen meg van határozva a
. Egy ilyen mátrixot sztochasztikus mátrixnak nevezünk.
Egy Markov-lánc egyértelműen meg van határozva a ![]() mátrix és a
mátrix és a ![]() kezdeti eloszlás megadásával. A
kezdeti eloszlás megadásával. A ![]() eloszlás meghatározására vezessük
be az
eloszlás meghatározására vezessük
be az ![]() lépéses átmenetvalószínűségek fogalmát.
Ezeket a következőképpen értelmezzük:
lépéses átmenetvalószínűségek fogalmát.
Ezeket a következőképpen értelmezzük:
![]()
A ![]() -lépéses átmenetvalószínűségek
kiszámítása a
-lépéses átmenetvalószínűségek
kiszámítása a ![]() átmenetvalószínűségek segítségével
történik a következő rekurzív képlet alapján:
átmenetvalószínűségek segítségével
történik a következő rekurzív képlet alapján:
![]()
amely a teljes valószínűség tétele alkalmazásával
igazolható. Speciálisan ![]() . Ha a
. Ha a ![]() átmenetvalószínűségeket is elrendezzük
mátrix alakban, úgy ez a mátrix
átmenetvalószínűségeket is elrendezzük
mátrix alakban, úgy ez a mátrix ![]() , azaz a
, azaz a ![]() mátrix
mátrix ![]() -edik hatványa lesz. Ez teljes indukcióval igazolható,
a mátrixok szorzási szabálya alapján, a fenti rekurzív
képlet tekintetbe vételével.
-edik hatványa lesz. Ez teljes indukcióval igazolható,
a mátrixok szorzási szabálya alapján, a fenti rekurzív
képlet tekintetbe vételével.
|