Azt mondjuk, hogy az
Azt mondjuk, hogy az ![]() állapot elérhető az
állapot elérhető az ![]() állapotból, ha létezik olyan
állapotból, ha létezik olyan ![]() , hogy
, hogy ![]() . Egy Markov-láncot irreducibilisnek nevezünk
akkor, ha minden állapota elérhető minden állapotából.
A nem irreducibilis Markov-láncok vizsgálata visszavezethető egymástól
független irreducibilis Markov-láncok tárgyalására.
Egy Markov-lánc állapotainak
. Egy Markov-láncot irreducibilisnek nevezünk
akkor, ha minden állapota elérhető minden állapotából.
A nem irreducibilis Markov-láncok vizsgálata visszavezethető egymástól
független irreducibilis Markov-láncok tárgyalására.
Egy Markov-lánc állapotainak ![]() halmazát zártnak mondjuk, ha egylépéses
átmenettel nem lehet kijutni ebből a halmazból, azaz
halmazát zártnak mondjuk, ha egylépéses
átmenettel nem lehet kijutni ebből a halmazból, azaz ![]() , ha
, ha ![]() , és
, és ![]() . Nyilvánvalóan ekkor tetszőleges
. Nyilvánvalóan ekkor tetszőleges ![]() -re is fennáll
-re is fennáll ![]() , ha
, ha ![]() és
és ![]() . Az irreducibilis Markov-láncok állapotai egyetlen
zárt halmazt alkotnak. Ha csupán egy zárt
. Az irreducibilis Markov-láncok állapotai egyetlen
zárt halmazt alkotnak. Ha csupán egy zárt ![]() halmaz állapotait tekintjük, úgy egy rész Markov-láncot
nyerünk, amely a többi állapottól függetlenül
vizsgálható. Egy Markov-láncot szétbonthatónak
mondunk, ha állapotai két vagy több zárt halmazra bomlanak.
Ha egyetlen
halmaz állapotait tekintjük, úgy egy rész Markov-láncot
nyerünk, amely a többi állapottól függetlenül
vizsgálható. Egy Markov-láncot szétbonthatónak
mondunk, ha állapotai két vagy több zárt halmazra bomlanak.
Ha egyetlen ![]() állapot képez egy zárt halmazt, akkor az
állapot képez egy zárt halmazt, akkor az ![]() állapotot abszorbeáló állapotnak nevezzük.
Ekkor
állapotot abszorbeáló állapotnak nevezzük.
Ekkor ![]() . Tekintsünk egy tetszőleges, de rögzített
. Tekintsünk egy tetszőleges, de rögzített ![]() állapotot. Tegyük fel, hogy a rendszer kezdetben
állapotot. Tegyük fel, hogy a rendszer kezdetben ![]() állapotban van
állapotban van ![]() . Jelölje
. Jelölje ![]() annak a valószínűségét, hogy az első visszatérés
az
annak a valószínűségét, hogy az első visszatérés
az ![]() állapotba az
állapotba az ![]() -edik lépésnél következik be
-edik lépésnél következik be ![]() . Az
. Az ![]() valószínűségek sorban meghatározhatók
a
valószínűségek sorban meghatározhatók
a
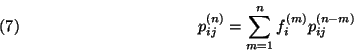


1. Tétel: Egy irreducibilis Markov-lánc állapotai mind ugyanazon osztályhoz tartoznak: vagy mind tranziensek, vagy rekurrens zérus állapotok, vagy rekurrens nem zérus állapotok. Mindegyik esetben az összes állapot periódusa megegyezik. Megjegyzés. Egy véges sok állapotú láncnak nem lehet zérus állapota, és nem lehet az összes állapota tranziens.
|