I.2.1.4. Nem periodikus Markov-lánc határeloszlás-tételei
Egy Markov-láncot ergodikusnak nevezünk, ha a 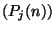 valószínűségeloszlások a kezdeti
valószínűségeloszlások a kezdeti 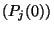 eloszlástól független
eloszlástól független 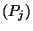 határeloszláshoz konvergálnak, azaz
határeloszláshoz konvergálnak, azaz 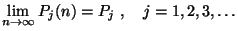 . A kezdeti
. A kezdeti
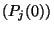 eloszlást stacionárius eloszlásnak mondjuk
abban az esetben, ha a
eloszlást stacionárius eloszlásnak mondjuk
abban az esetben, ha a 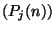 eloszlások megegyeznek a kezdeti eloszlással.
2. Tétel: Tegyük fel, hogy egy irreducibilis
Markov-lánc állapotai nem periodikusak, nem tranziensek, és nem
zérus állapotok. Ekkor
eloszlások megegyeznek a kezdeti eloszlással.
2. Tétel: Tegyük fel, hogy egy irreducibilis
Markov-lánc állapotai nem periodikusak, nem tranziensek, és nem
zérus állapotok. Ekkor 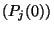 kezdeti eloszlástól függetlenül léteznek
a
kezdeti eloszlástól függetlenül léteznek
a
határértékek. Továbbá 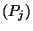 egy valószínűségeloszlás pozitív elemekkel,
azaz
egy valószínűségeloszlás pozitív elemekkel,
azaz
A 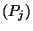 valószínűségeloszlás egyértelműen meghatározható
az alábbi lineáris egyenletrendszer segítségével:
valószínűségeloszlás egyértelműen meghatározható
az alábbi lineáris egyenletrendszer segítségével:
Végül fennáll, hogy az 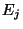 állapot átlagos visszatérési ideje,
állapot átlagos visszatérési ideje, 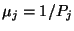 .
Megjegyezzük, hogy ha egy irreducibilis Markov-lánc állapotai nem
periodikusak, de az összes állapotai tranziensek vagy zérus állapotok,
úgy a kezdeti eloszlástól függetlenül fennáll
.
Megjegyezzük, hogy ha egy irreducibilis Markov-lánc állapotai nem
periodikusak, de az összes állapotai tranziensek vagy zérus állapotok,
úgy a kezdeti eloszlástól függetlenül fennáll 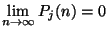 .
Megemlítünk néhány kritériumot egy Markov-lánc ergodikus
voltának eldöntésére. A. A. Markov tétele szerint véges
sok állapottal bíró, nem periodikus és irreducibilis Markov-lánc
állapotai ergodikusak, és így érvényes a 2. Tétel.
Egy tetszőleges, nem periodikus és irreducibilis Markov-lánc ergodikus,
ha a
.
Megemlítünk néhány kritériumot egy Markov-lánc ergodikus
voltának eldöntésére. A. A. Markov tétele szerint véges
sok állapottal bíró, nem periodikus és irreducibilis Markov-lánc
állapotai ergodikusak, és így érvényes a 2. Tétel.
Egy tetszőleges, nem periodikus és irreducibilis Markov-lánc ergodikus,
ha a 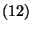 alatti
alatti
egyenletrendszernek létezik olyan nem zérus megoldása, amelyre
A 2. Tételből következik, hogy ha a Markov-lánc ergodikus, úgy
egyetlen stacionárius eloszlás létezik, éspedig ez a 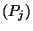 határeloszlással egyezik meg. Ha pedig egy irreducibilis
és nem periodikus Markov-lánc állapotai tranziensek vagy zérus
állapotok, úgy nem létezik stacionárius eloszlás. Fizikai
rendszereknél a statisztikai egyensúly-állapotot a stacionárius
eloszlással írjuk le, és azt a tényt, hogy a
határeloszlással egyezik meg. Ha pedig egy irreducibilis
és nem periodikus Markov-lánc állapotai tranziensek vagy zérus
állapotok, úgy nem létezik stacionárius eloszlás. Fizikai
rendszereknél a statisztikai egyensúly-állapotot a stacionárius
eloszlással írjuk le, és azt a tényt, hogy a 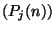 eloszlások konvergálnak a
eloszlások konvergálnak a 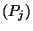 határeloszláshoz, úgy értelmezzük, mint
az egyensúlyi állapothoz való közeledést.
határeloszláshoz, úgy értelmezzük, mint
az egyensúlyi állapothoz való közeledést.
![]()
![]()
![]()
![]()
![]() határeloszlással egyezik meg. Ha pedig egy irreducibilis
és nem periodikus Markov-lánc állapotai tranziensek vagy zérus
állapotok, úgy nem létezik stacionárius eloszlás. Fizikai
rendszereknél a statisztikai egyensúly-állapotot a stacionárius
eloszlással írjuk le, és azt a tényt, hogy a
határeloszlással egyezik meg. Ha pedig egy irreducibilis
és nem periodikus Markov-lánc állapotai tranziensek vagy zérus
állapotok, úgy nem létezik stacionárius eloszlás. Fizikai
rendszereknél a statisztikai egyensúly-állapotot a stacionárius
eloszlással írjuk le, és azt a tényt, hogy a ![]() eloszlások konvergálnak a
eloszlások konvergálnak a ![]() határeloszláshoz, úgy értelmezzük, mint
az egyensúlyi állapothoz való közeledést.
határeloszláshoz, úgy értelmezzük, mint
az egyensúlyi állapothoz való közeledést.