Tekintsük a
Tekintsük a ![]() paraméter véges vagy végtelen intervallumba eső értékeire
értelmezett valós
paraméter véges vagy végtelen intervallumba eső értékeire
értelmezett valós ![]() valószínűségi változók összeségét.
A
valószínűségi változók összeségét.
A ![]() sztochasztikus folyamatot Markov-folyamatnak nevezzük,
ha fennáll
sztochasztikus folyamatot Markov-folyamatnak nevezzük,
ha fennáll
![]()
![]()
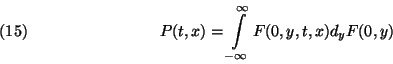
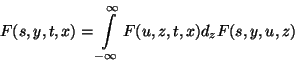
ún. Chapman-Kolmogorov egyenlet, ahol ![]() . A
. A ![]() Markov-folyamatot ergodikusnak nevezzük, ha létezik
a
Markov-folyamatot ergodikusnak nevezzük, ha létezik
a ![]() határeloszlásfüggvény
és független
határeloszlásfüggvény
és független ![]() -tól. Ekkor
-tól. Ekkor ![]() is létezik és az előzővel
megegyezik. A
is létezik és az előzővel
megegyezik. A ![]() változó
változó ![]() eloszlását stacionáriusnak mondjuk, ha
eloszlását stacionáriusnak mondjuk, ha
![]() . A
. A ![]() Markov-folyamatot osztályozhatjuk még aszerint is,
hogy
Markov-folyamatot osztályozhatjuk még aszerint is,
hogy ![]() értékkészlete diszkrét vagy
értékkészlete diszkrét vagy ![]() változása folytonos, vagy
változása folytonos, vagy ![]() változása folytonos és ugrásszerű lehet.
változása folytonos és ugrásszerű lehet.
|