II.5.1. Az <n/M/M/1> modell
Feltesszük, hogy az igények egy 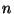 elemű véges forrásból érkeznek, ahol a forrásban
eltöltött idő minden igény esetén egymástól független
elemű véges forrásból érkeznek, ahol a forrásban
eltöltött idő minden igény esetén egymástól független
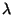 paraméterű exponenciális eloszlású valószínűségi
változó. A kiszolgálási idők szintén exponenciális
eloszlásúak
paraméterű exponenciális eloszlású valószínűségi
változó. A kiszolgálási idők szintén exponenciális
eloszlásúak 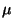 paraméterrel és függetlenek az előbbi valószínűségi
változóktól. Jelölje
paraméterrel és függetlenek az előbbi valószínűségi
változóktól. Jelölje 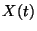 a
a 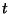 időpillanatban a kiszolgáló egységnél tartózkodó
igények számát. Az előbbiekhez hasonlóan nem nehéz
belátni, hogy
időpillanatban a kiszolgáló egységnél tartózkodó
igények számát. Az előbbiekhez hasonlóan nem nehéz
belátni, hogy 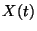 is egy születési-kihalási folyamat
is egy születési-kihalási folyamat
születési intenzitásokkal, és
kihalási intenzitással. Így
ahol
és
Az ergodikus eloszlás mindig létezik, de ha 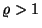 akkor az igények torlódnak és több
kiszolgálóegységre lenne szükség. Az előbbi valószínűségekre
egy másik kifejezést is megadunk, amely numerikus számításoknál
könnyebben alkalmazható. Legyen
akkor az igények torlódnak és több
kiszolgálóegységre lenne szükség. Az előbbi valószínűségekre
egy másik kifejezést is megadunk, amely numerikus számításoknál
könnyebben alkalmazható. Legyen 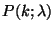 a
a 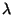 paraméterű Poisson-eloszlás és
paraméterű Poisson-eloszlás és 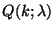 ennek kummulatív eloszlása, azaz
ennek kummulatív eloszlása, azaz
Megmutatjuk, hogy
ahol
Ugyanis
Az n/M/M/1 rendszer jellemzői:
(I.) A szerver kihasználtsága és a rendszer átbocsátóképessége:
A szerver kihasználtsága:
A korábbi rekurzív ös<szefüggést felhasználva
A rendszer átbocsátóképessége:
(II.) A rendszerben tartózkodó igények átlagos száma:
Másképpen:
(III.) Az átlagos sorhossz:
(IV.) Az igénygenerálásra alkalmas teminálok átlagos
száma:
(V.) A szerver átlagos foglaltsági periódushossza: Mivel
ezért
(VI.) A várakozás valószínűsége:
Számítógépes alkalmazásoknál gyakran szükségünk
van az alábbi jellemzőkre is.
(VII.) A terminálok kihasználtsága:
Véges forrás esetén szükségünk van arra az újabb
mérőszámra is , amely a gépkiszolgálási probléma
esetén is nagyon fontos. Az 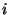 indexű terminál kihasználtságán az
indexű terminál kihasználtságán az
határértéket értjük, ha létezik. Ekkor (5) szerint
ahol P a stacionárius valószínűséget jelöli.
Nyilvánvaló, hogy a terminálok (az igénygenerálás
forrásai) akkor vannak kihasználva, ha működnek, így az
összes terminál kihasználtsága:
Egy tetszőleges terminál kihasználtsága:
Ezt az összefüggést a következőképpen is megkaphatjuk.
Látható, hogy
mivel a terminálok azonos kihasználtságúak, így
(VIII.) A terminálok átlagos várakozási ideje:
(5) alapján:
Ebből
és
ami az átlagos sorhosszra vonatkozó Little-formula. Így
Az átlagos válaszolási idő:
Egyszerű számolással könnyű bebizonyítani, hogy
ami ismét egy Little-formula. Ugyanis
(IX.) További összefüggések:
melyből
Példák:
1. Tekintsünk 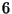 db. gépet
db. gépet 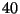 óra átlagos élettartammal, javítási idejük
4 óra átlagosan. Határozzuk meg a rendszer jellemzőit!
Megoldás:
óra átlagos élettartammal, javítási idejük
4 óra átlagosan. Határozzuk meg a rendszer jellemzőit!
Megoldás: 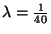 óránként,
óránként, 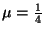 óránként,
óránként, 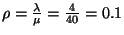 ,
, 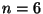 ,
, 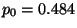
2. Az előző feladatban az átlagos élettartamot változtassuk meg
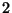 órára. Határozzuk meg a rendszer jellemzőit!
órára. Határozzuk meg a rendszer jellemzőit!
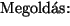
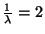 ,
, 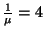 ,
, 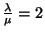 ,
, 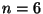 ,
, 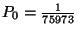 amiből látható, hogy egy szerelő nem elégséges.
amiből látható, hogy egy szerelő nem elégséges.
Mivel a karbantartási tényező 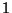 -nél nagyobb, minden adat azt mutatja, amit vártunk. Arra,
hogy ezek után mennyi szerelőt kell beállítani, többféle
kritérium lehet. Ezzel a következő fejezetben foglalkozunk. Mindenesetre,
hogy ne legyen torlódás, a
-nél nagyobb, minden adat azt mutatja, amit vártunk. Arra,
hogy ezek után mennyi szerelőt kell beállítani, többféle
kritérium lehet. Ezzel a következő fejezetben foglalkozunk. Mindenesetre,
hogy ne legyen torlódás, a 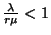 feltételnek kell teljesülnie, ahol
feltételnek kell teljesülnie, ahol
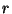 a szerelők számát jelöli.
a szerelők számát jelöli.
![]() elemű véges forrásból érkeznek, ahol a forrásban
eltöltött idő minden igény esetén egymástól független
elemű véges forrásból érkeznek, ahol a forrásban
eltöltött idő minden igény esetén egymástól független
![]() paraméterű exponenciális eloszlású valószínűségi
változó. A kiszolgálási idők szintén exponenciális
eloszlásúak
paraméterű exponenciális eloszlású valószínűségi
változó. A kiszolgálási idők szintén exponenciális
eloszlásúak ![]() paraméterrel és függetlenek az előbbi valószínűségi
változóktól. Jelölje
paraméterrel és függetlenek az előbbi valószínűségi
változóktól. Jelölje ![]() a
a ![]() időpillanatban a kiszolgáló egységnél tartózkodó
igények számát. Az előbbiekhez hasonlóan nem nehéz
belátni, hogy
időpillanatban a kiszolgáló egységnél tartózkodó
igények számát. Az előbbiekhez hasonlóan nem nehéz
belátni, hogy ![]() is egy születési-kihalási folyamat
is egy születési-kihalási folyamat 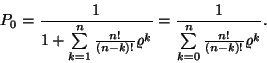
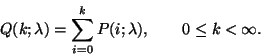
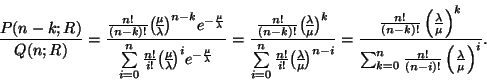
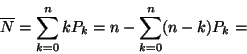
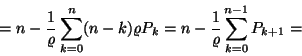
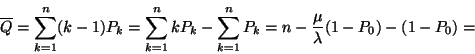
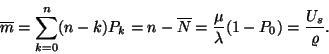
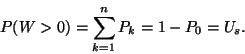
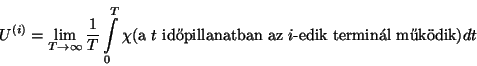
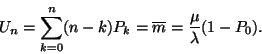
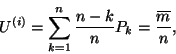


![]() -nél nagyobb, minden adat azt mutatja, amit vártunk. Arra,
hogy ezek után mennyi szerelőt kell beállítani, többféle
kritérium lehet. Ezzel a következő fejezetben foglalkozunk. Mindenesetre,
hogy ne legyen torlódás, a
-nél nagyobb, minden adat azt mutatja, amit vártunk. Arra,
hogy ezek után mennyi szerelőt kell beállítani, többféle
kritérium lehet. Ezzel a következő fejezetben foglalkozunk. Mindenesetre,
hogy ne legyen torlódás, a ![]() feltételnek kell teljesülnie, ahol
feltételnek kell teljesülnie, ahol
![]() a szerelők számát jelöli.
a szerelők számát jelöli.