II.5.2. Az <n/M/M/r> modell
Az előző modellben adott feltevéseinke<t most csupán annyiban változtatjuk,
hogy az 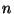 számú terminált
számú terminált 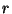 szerver szolgálja ki
szerver szolgálja ki 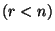 . Így
. Így 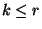 esetén a
esetén a 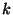 állapot azt jelenti, hogy éppen
állapot azt jelenti, hogy éppen 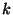 db terminál igénye van kiszolgálás alatt, egyetlen
várakozó igény sincs és
db terminál igénye van kiszolgálás alatt, egyetlen
várakozó igény sincs és 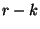 szerver tétlen. A szerverek tevékenységüket
egymástól függetlenül végzik. Ekkor is egy születési-halálozási
folyamatot kapunk:
szerver tétlen. A szerverek tevékenységüket
egymástól függetlenül végzik. Ekkor is egy születési-halálozási
folyamatot kapunk:
intenzitásokkal. Az egyensúlyi eloszlás:
Természetesen teljesülnmie kell a
összefüggésnek. 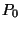 meghatározására ez a képlet túlságosan
bonyolult, így egy egyszerűbb rekurzív formulát használunk.
Jelöljük
meghatározására ez a képlet túlságosan
bonyolult, így egy egyszerűbb rekurzív formulát használunk.
Jelöljük 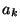 -val a következő hányadost:
-val a következő hányadost:
Ekkor a következő összefüggés alapján számolhatunk
Mivel a
összefüggésnek teljesülnie kell, ezért
Mindkét oldalt 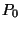 -al elosztva:
-al elosztva:
így
Majd
Az n/M/M/r rendszer jellemzői:
(I.) A rendszerben tartózkodó igények átlagos száma:
(II.) A várakozási sor átlagos hossza:
(III.) Az igénygenerálásra alkalmas terminálok átlagos
száma:
(IV.) A rendszer kihasználtsága:
(V.) A rendszer átlagos foglaltsági periódushossza:
(VI.) A várakozás valószínűsége:
(VII.) A foglalt kiszolgálóegységek átlagos száma:
Továbbá
(VIII.) A tétlen kiszolgálóegységek átlagos száma:
További összefüggés:
(IX.) A terminálok kihasználtsága:
(X.) A terminálok átlagos várakozási ideje: (5) és
(IX) alapján
amiből
Az átlagos válaszolási idő:
innen
ami a jól ismert Little-formula, azaz az átlagos beérkezési
intenzitás és a rendszerben töltött átlagos idő szorzata
a rendszerben tartózkodó igények átlagos számával
egyenlő. Ebből
vagyis
Mutassuk meg, hogy
mert ebből
következik, ami szintén egy Little-formula. Tudjuk, hogy
ahol
Jól ismert továbbá, hogy
Ekkor
Vagyis
más alakban
azaz
ami várható volt, mivel a rendszer egyensúlyi állapotban van.
Ezért
(XI.) A kiszolgálók átlagos tétlenségi periódushossza:
Ha a tétlen kiszolgálók olyan sorrendben kezdik kiszolgálni
az igényeket, mint amilyen sorrendben előzőleg befejezték a foglaltsági
periódusokat, akkor egy szerver tevékenységét a következőképpen
írhatjuk le. Ha egy tétlenné vált szerver 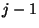 másik tétlen szervert talál a munkabefejeződés
pillanatában, akkor csak a
másik tétlen szervert talál a munkabefejeződés
pillanatában, akkor csak a 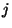 -edik igény kiszolgálásával kezdődik ismét
a foglaltsági periódusa. Jelölje
-edik igény kiszolgálásával kezdődik ismét
a foglaltsági periódusa. Jelölje 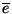 a szerver átlagos üresjárati periódusa
hosszát,
a szerver átlagos üresjárati periódusa
hosszát, 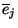 pedig a fenti állapotban az átlagos tétlenségi
időt. Nyilvánvalóan
pedig a fenti állapotban az átlagos tétlenségi
időt. Nyilvánvalóan
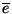 pedig a teljes várható érték tétele
alapján
pedig a teljes várható érték tétele
alapján
ahol
azaz annak valószínűsége, hogy van tétlen szerver.
(XII.) A szerverek átlagos foglaltsági periódushossza:
Mivel
így
Vagyis
Példák:
1. Egy üzemben 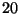 db gép üzemel, egyenként
db gép üzemel, egyenként 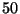 óra átlagos élettartammal. A gép javításának
várható értéke
óra átlagos élettartammal. A gép javításának
várható értéke 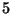 óra. A szereléseket
óra. A szereléseket 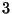 fős szerelőgárda végzi. Adjuk meg a rendszer jellemzőit,
és hasonlítsuk össze őket a II.5.1.1. Példában szereplő
jellemzőkkel!
Megoldás:
fős szerelőgárda végzi. Adjuk meg a rendszer jellemzőit,
és hasonlítsuk össze őket a II.5.1.1. Példában szereplő
jellemzőkkel!
Megoldás:
A rekurzív összefüggéseket használva, 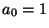 -ről indítva a rekurziót, könnyen meghatározhatjuk
az
-ről indítva a rekurziót, könnyen meghatározhatjuk
az 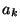 értékeket, pl
értékeket, pl
és így tovább. Tudjuk, hogy
Innen
A következő táblázat megadja a különböző állapotok
valószínűségét.  ,
,  ,
,  -10pt
-10pt
Összëehasonlítva a II.5.1 1. Példában szereplő jellemzőkkel,
láthatjuk, hogy az egy szerelőre jutó gépek majdnem egyforma száma
mellett (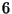 ill.
ill.  ) a helyzet sokkal jobb
) a helyzet sokkal jobb 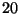 gép és
gép és 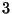 szerelő esetében, ugyanis a hatékon<ysági vizsgálatok
az alábbi adatokat szolgáltatták:
szerelő esetében, ugyanis a hatékon<ysági vizsgálatok
az alábbi adatokat szolgáltatták:
2. Az előző példában  ,
,  volt. Tételezzük fel, hogy az időegység az óra,
a gépállás óránkénti költsége
volt. Tételezzük fel, hogy az időegység az óra,
a gépállás óránkénti költsége  Ft, míg a szerelők óránkénti költsége
Ft, míg a szerelők óránkénti költsége
 Ft. Mi lesz ebben ez esetben a szerelők optimális száma,
ha az átlagos veszteség minimalizálására törekszünk?
Ft. Mi lesz ebben ez esetben a szerelők optimális száma,
ha az átlagos veszteség minimalizálására törekszünk?
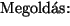 Látható, hogy az óránkénti
átlagos költség
Látható, hogy az óránkénti
átlagos költség 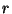 függvénye. A következő táblázat megadja a
stacionárius eloszlást
függvénye. A következő táblázat megadja a
stacionárius eloszlást  esetén (tapasztalatból tudjuk, hogy az
esetén (tapasztalatból tudjuk, hogy az 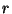 számra
számra  ).
).
A következő táblázat az időegységre jutó átlagos
költségeket adja meg:
Látható, hogy az optimális szerelőszám ilyen költségtényezők
mellett  . Ez a példa is mutatja, hogy rendszerek összehasonlítása
többféleképpen értelmezhető. Az
. Ez a példa is mutatja, hogy rendszerek összehasonlítása
többféleképpen értelmezhető. Az  és
és  példa jól szemlélteti ezen problémakört.
példa jól szemlélteti ezen problémakört.
![]() számú terminált
számú terminált ![]() szerver szolgálja ki
szerver szolgálja ki ![]() . Így
. Így ![]() esetén a
esetén a ![]() állapot azt jelenti, hogy éppen
állapot azt jelenti, hogy éppen ![]() db terminál igénye van kiszolgálás alatt, egyetlen
várakozó igény sincs és
db terminál igénye van kiszolgálás alatt, egyetlen
várakozó igény sincs és ![]() szerver tétlen. A szerverek tevékenységüket
egymástól függetlenül végzik. Ekkor is egy születési-halálozási
folyamatot kapunk:
szerver tétlen. A szerverek tevékenységüket
egymástól függetlenül végzik. Ekkor is egy születési-halálozási
folyamatot kapunk: 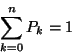
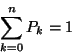
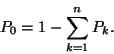
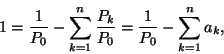
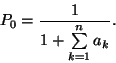
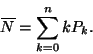
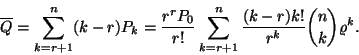
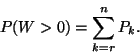
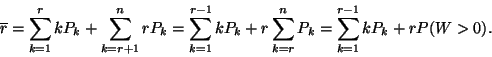
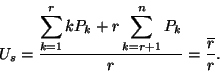
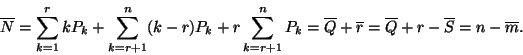
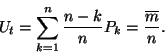
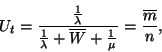
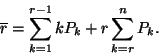
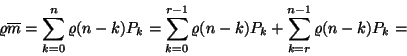
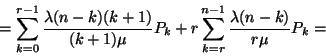
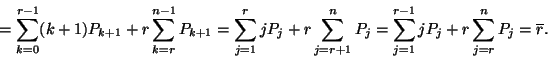
![]() másik tétlen szervert talál a munkabefejeződés
pillanatában, akkor csak a
másik tétlen szervert talál a munkabefejeződés
pillanatában, akkor csak a ![]() -edik igény kiszolgálásával kezdődik ismét
a foglaltsági periódusa. Jelölje
-edik igény kiszolgálásával kezdődik ismét
a foglaltsági periódusa. Jelölje ![]() a szerver átlagos üresjárati periódusa
hosszát,
a szerver átlagos üresjárati periódusa
hosszát, ![]() pedig a fenti állapotban az átlagos tétlenségi
időt. Nyilvánvalóan
pedig a fenti állapotban az átlagos tétlenségi
időt. Nyilvánvalóan 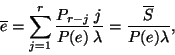
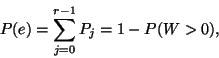
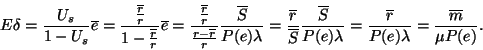
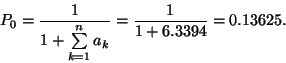




![]() . Ez a példa is mutatja, hogy rendszerek összehasonlítása
többféleképpen értelmezhető. Az
. Ez a példa is mutatja, hogy rendszerek összehasonlítása
többféleképpen értelmezhető. Az ![]() és
és ![]() példa jól szemlélteti ezen problémakört.
példa jól szemlélteti ezen problémakört.