III.1.3. Az átmeneti valószínűségek és a sorhossz várható értéke
A következő fejezetekben a rendszerre jellemző mennyiségeket számoljuk
ki. Először is bevezetünk néhány jelölést, amelyekre
a későbbiekben szükségünk lesz. 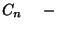 a rendszerbe belépő
a rendszerbe belépő 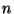 -edik igény;
-edik igény; 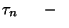 a
a 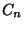 igény beérkezési ideje;
igény beérkezési ideje; 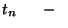
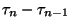 , a
, a 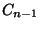 és
és 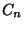 igények beérkezése közötti időtartam;
igények beérkezése közötti időtartam; 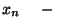 a
a 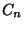 igény kiszolgálási ideje;
igény kiszolgálási ideje; 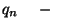 a
a 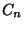 igény távozásakor hátrahagyott igények
száma;
igény távozásakor hátrahagyott igények
száma; 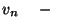 a
a 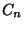 igény kiszolgálása alatt a rendszerbe érkező
új igények száma.
igény kiszolgálása alatt a rendszerbe érkező
új igények száma.
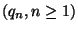 az ú.n. beágyazott Markov-lánc, amelynek
egylépéses átmenetvalószínűségei:
az ú.n. beágyazott Markov-lánc, amelynek
egylépéses átmenetvalószínűségei:
Elsősorban a 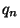 eloszlását vizsgáljuk, vagyis a
eloszlását vizsgáljuk, vagyis a 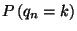 valószínűségeket. Ezek függenek
az időtől, határeloszlásukat (ha
valószínűségeket. Ezek függenek
az időtől, határeloszlásukat (ha 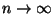 ),
), 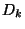 -val jelöljük. A
-val jelöljük. A 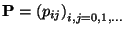 átmenetvalószínűségi
mátrix a következő alakú lesz:
átmenetvalószínűségi
mátrix a következő alakú lesz:
ahol 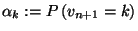 . Az
. Az 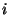 -edik sor
-edik sor 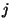 -edik eleme annak a valószínűségét adja meg, hogy
ha
-edik eleme annak a valószínűségét adja meg, hogy
ha 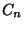 távozásakor
távozásakor 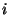 igényt hagyott maga után a rendszerben, akkor
igényt hagyott maga után a rendszerben, akkor 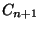 távozásakor éppen
távozásakor éppen 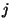 igény maradt a rendszerben. Ez éppen azt jelenti, hogy pontosan
igény maradt a rendszerben. Ez éppen azt jelenti, hogy pontosan
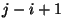 új igény érkezett, amíg a
új igény érkezett, amíg a 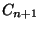 igény kiszolgálása tartott. Az
igény kiszolgálása tartott. Az 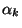 kiszámolásához vegyük figyelembe, hogy
a beérkezési folyamat független a rendszer állapotától.
A
kiszámolásához vegyük figyelembe, hogy
a beérkezési folyamat független a rendszer állapotától.
A 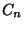 igény, (
igény, (  eloszlású),
eloszlású), 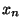 kiszolgálási ideje pedig független az
kiszolgálási ideje pedig független az 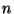 -től, ezért
-től, ezért 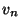 szintén független az
szintén független az 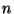 értékétől. Hagyjuk el tehát az
értékétől. Hagyjuk el tehát az 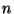 -et a jelölésünkből és vezessük be az
-et a jelölésünkből és vezessük be az 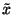 és
és 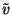 valószínűségi változókat.
valószínűségi változókat. 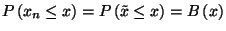 és
és 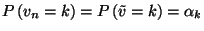 . A teljes valószínűség
tétele alapján
. A teljes valószínűség
tétele alapján
melyet a feltételes valószínűségekkel kifejezve
ahol 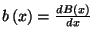 , a kiszolgálási
idő sűrűségfüggvénye. Mivel a beérkezési folyamat
, a kiszolgálási
idő sűrűségfüggvénye. Mivel a beérkezési folyamat 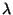 paraméterű Poisson-folyamat, ahol
paraméterű Poisson-folyamat, ahol 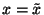 az időváltozó, a következő átmenetvalószínűségeket
(
az időváltozó, a következő átmenetvalószínűségeket
(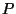 elemeit) kapjuk:
elemeit) kapjuk:
Figyelembe véve, hogy 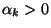 minden
minden 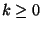 -ra, a
-ra, a 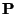 mátrix alakjából következik, hogy bármely
adott állapotból az összes többi elérhető, azaz a Markov-lánc
irreducibilis (és aperiodikus). A sorbanállási elmélet alapjainál
használt szokásos jelöléssel
mátrix alakjából következik, hogy bármely
adott állapotból az összes többi elérhető, azaz a Markov-lánc
irreducibilis (és aperiodikus). A sorbanállási elmélet alapjainál
használt szokásos jelöléssel
ahol 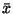 a kiszolgálási idő hosszának várható
értéke. A Markov-lánc ergodikus, ha
a kiszolgálási idő hosszának várható
értéke. A Markov-lánc ergodikus, ha  . (A továbbiakban ezt feltételezzük.) Most
vizsgáljuk a
. (A továbbiakban ezt feltételezzük.) Most
vizsgáljuk a 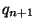 és
és 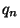 valószínűségi változók kapcsolatát
két speciális esetben. Az első annak felel meg, amikor
valószínűségi változók kapcsolatát
két speciális esetben. Az első annak felel meg, amikor 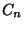 nem üres rendszert hagy maga után (azaz
nem üres rendszert hagy maga után (azaz 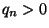 ). Ez azt jelenti, hogy a
). Ez azt jelenti, hogy a 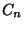 távozásakor a
távozásakor a 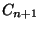 már a rendszerben van. Ekkor
már a rendszerben van. Ekkor 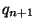 nyilván megkapható, ha
nyilván megkapható, ha 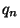 -ből levonunk egyet (mivel
-ből levonunk egyet (mivel 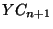 eltávozik) és hozzáadjuk azon igények számát,
melyek az
eltávozik) és hozzáadjuk azon igények számát,
melyek az 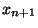 kiszolgálási időtartam alatt érkeztek be, azaz
kiszolgálási időtartam alatt érkeztek be, azaz
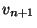 -et. A második eset az, amikor
-et. A második eset az, amikor  , azaz a távozó
, azaz a távozó 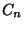 igény üres rendszert hagy maga után, azaz
igény üres rendszert hagy maga után, azaz 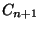 nem érkezett meg a
nem érkezett meg a 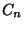 távozási időpontjáig. Így
távozási időpontjáig. Így 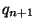 éppen a
éppen a 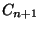 kiszolgálási ideje alatt a rendszerbe érkezett
igények számával egyenlő. Végeredményben azt kaptuk,
hogy
kiszolgálási ideje alatt a rendszerbe érkezett
igények számával egyenlő. Végeredményben azt kaptuk,
hogy
Vezessük be a
mennyiségeket. Ennek segítségével
Ebből az egyenletből határozzuk meg a 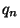 várható értékét. Először nem az időtől
függő viselkedéssel foglalkozunk, hanem a határeloszlással
(feltéve a létezését), azaz
várható értékét. Először nem az időtől
függő viselkedéssel foglalkozunk, hanem a határeloszlással
(feltéve a létezését), azaz 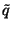 -mal. Tegyük fel, hogy léteznek a
-mal. Tegyük fel, hogy léteznek a 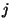 -edik momentumok is és
-edik momentumok is és
(Ismét az ergodikusságot használva.) Formális számolással
vegyük 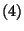 mindkét oldalának várható értékét
és végezzük el az
mindkét oldalának várható értékét
és végezzük el az 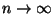 határátmenetet.
határátmenetet.
Ebből
Tudjuk, hogy 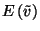 a beérkezések átlagos száma
egy igény kiszolgálási ideje alatt.
a beérkezések átlagos száma
egy igény kiszolgálási ideje alatt.  bal oldala definíció szerint
bal oldala definíció szerint
Mivel egyetlen kiszolgáló csatornánk van,
A 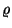 kihasználtsági tényező pedig éppen a rendszer
foglaltságának valószínűségét adja meg, ezért
kihasználtsági tényező pedig éppen a rendszer
foglaltságának valószínűségét adja meg, ezért
Így  alapján
alapján
Tehát az egy igény kiszolgálási ideje alatti beérkezések
számának várható értéke 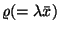 . A stabilitáshoz megkövetelt
. A stabilitáshoz megkövetelt  miatt a (6) egyenlethez szükséges, hogy az igényeknek
lassabban kell érkezniük, mint ahogyan a kiszolgálás történik.
miatt a (6) egyenlethez szükséges, hogy az igényeknek
lassabban kell érkezniük, mint ahogyan a kiszolgálás történik.
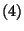 négyzetre emelésével
négyzetre emelésével
Nyilvánvaló, hogy 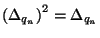 és
és 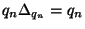 , így
, így
Mivel 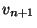 független
független 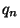 -től, a két utolsó tag várható értékét
mint várható értékek szorzatát lehet felírni.
-től, a két utolsó tag várható értékét
mint várható értékek szorzatát lehet felírni. 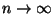 határátmenetet véve
határátmenetet véve
 -öt és
-öt és 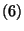 -ot kihasználva kifejezhetjük
-ot kihasználva kifejezhetjük 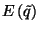 -ot.
-ot.
ahonnan
(7)-ben már csak ismeretlen. Ennek meghatározásához egy általános
módszert, a generátorfüggvények módszerét használjuk.
Legyen a 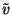 változó generátorfüggvénye.
változó generátorfüggvénye.
Innen 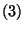 felhasználásával
felhasználásával
Legyen 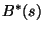 a kiszolgálási idő sűrűségfüggvényének
Laplace-transzformáltja, vagyis
a kiszolgálási idő sűrűségfüggvényének
Laplace-transzformáltja, vagyis
A következő hasznos összefüggést vehetjük észre
az előző két egyenlet között:
Mint ismert, a generátorfüggvény deriváltjainak a 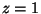 helyen vett helyettesítési értékei, valamint
a Laplace-transzformált
helyen vett helyettesítési értékei, valamint
a Laplace-transzformált 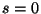 helyen vett helyettesítési értékei a vizsgált
valószínűségi változó megfelelő momentumait adják
meg. A valószínűségi változó várható értékére
a felülvonással való jelölést használva, a következőket
írhatjuk:
helyen vett helyettesítési értékei a vizsgált
valószínűségi változó megfelelő momentumait adják
meg. A valószínűségi változó várható értékére
a felülvonással való jelölést használva, a következőket
írhatjuk:
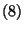 -ból láthatóan
-ból láthatóan
ahol 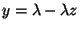 . Végezzük el a
. Végezzük el a 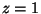 helyettesítést. Ekkor
helyettesítést. Ekkor
mivel 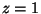 -nél
-nél 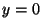 adódik. Ebből
adódik. Ebből 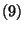 -et és
-et és  -et felhasználva
-et felhasználva
amit már az előzőekből ismerünk. Most differenciáljuk még
egyszer  -t:
-t:
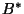 első deriváltját felhasználva a másodikra az
alábbi összefüggés adódik:
első deriváltját felhasználva a másodikra az
alábbi összefüggés adódik:
f 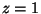 -et helyettesítve
-et helyettesítve
A korábbiakból
A további momentumok is hasonlóan határozhatók meg. Térjünk
vissza 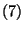 -hez és alkalmazzuk az előző összefüggést, adódik
-hez és alkalmazzuk az előző összefüggést, adódik
Mivel 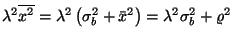 , ahol
, ahol 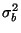 a kiszolgálási idő szórásnégyzete,
a kiszolgálási idő szórásnégyzete,
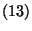 más alakban:
más alakban:
Ez a keresett formula, ami az átlagos sorhosszat, azaz az 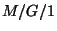 rendszerben tartózkodó igények számának
várható értékét adja meg ismert mennyiségek segítségével.
Ezt Pollaczek-Hincsin-féle (P-H) várható érték-formulának
nevezzük. A P-H várható érték-formula a
rendszerben tartózkodó igények számának
várható értékét adja meg ismert mennyiségek segítségével.
Ezt Pollaczek-Hincsin-féle (P-H) várható érték-formulának
nevezzük. A P-H várható érték-formula a 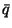 mennyiségekre, a távozási pillanatokban a rendszerben
tartózkodó igények számának várható értékére
ad egy kifejezést. De tudjuk, hogy aérkezési pillanatokban, sőt
bármelyik pillanatban is ez a várható érték. Az általában
használt jelölés szerint
mennyiségekre, a távozási pillanatokban a rendszerben
tartózkodó igények számának várható értékére
ad egy kifejezést. De tudjuk, hogy aérkezési pillanatokban, sőt
bármelyik pillanatban is ez a várható érték. Az általában
használt jelölés szerint 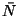 jelenti ezt a mennyiséget. Vezessük be most
jelenti ezt a mennyiséget. Vezessük be most 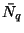 -t a sorbanálló igények számának várható
értékeként (ez nem tartalmazza a kiszolgálócsatornában
lévő igényt).
-t a sorbanálló igények számának várható
értékeként (ez nem tartalmazza a kiszolgálócsatornában
lévő igényt).
Innen
Bebizonyítunk egy általános eredményt, az első Little-formulát,
ami a beérkezési intenzitás, a rendszerben tartózkodó
igények számának várható értéke és az
igények rendszerbeli idejének várható értéke között
ad meg egy egyszerű összefüggést. Legyen 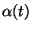 a
a 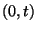 intervallum alatt beérkezett igények száma,
intervallum alatt beérkezett igények száma, 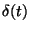 a
a 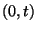 intervallum alatt a rendszerből kilépett igények száma.
intervallum alatt a rendszerből kilépett igények száma.
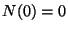 -t feltéve nyilvánvalóan
-t feltéve nyilvánvalóan 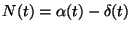 . Jelölje a
. Jelölje a 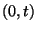 intervallumban a beérkezési intenzitást
intervallumban a beérkezési intenzitást
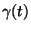 legyen a
legyen a 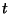 pillanatig felgyűlt összes igényidő, pontosabban az az idő,
amit a
pillanatig felgyűlt összes igényidő, pontosabban az az idő,
amit a 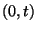 időtartam során az igények összesen eltöltöttek
a rendszerben. A
időtartam során az igények összesen eltöltöttek
a rendszerben. A 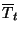 mennyiség legyen az egy igényre eső rendszerbeli
idő átlaga, a
mennyiség legyen az egy igényre eső rendszerbeli
idő átlaga, a 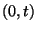 intervallum összes igényét figyelembe véve.
Ezekből nyilván
intervallum összes igényét figyelembe véve.
Ezekből nyilván
Végül legyen 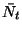 a rendszerben tartózkodó igények átlagos
száma a
a rendszerben tartózkodó igények átlagos
száma a 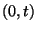 intervallumban:
intervallumban:
Az utolsó három egyenletből
Sorbanállási rendszerünkben (ergodikusság esetén) léteznek
az alábbi határértékek
Így (Little-formula)
Most levezetünk egy eredményt a rendszerben eltöltött átlagos
időre. Ha felhasználjuk a fenti Little-formulát, 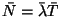 -t, valamint
-t, valamint 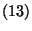 -at, és tudjuk, hogy
-at, és tudjuk, hogy 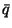 egy találomra választott időpontra is megadja a rendszerben
található igények számának várható értékét,
azaz
egy találomra választott időpontra is megadja a rendszerben
található igények számának várható értékét,
azaz 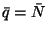 , akkor
, akkor
Innen
Ez egy igény rendszerben eltöltött összidejének átlaga,
ami egyenlő az átlagos kiszolgálási időnek, valamint a sorbanállási
idő átlagának összegével, amit 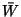 -vel jelölünk. Így
-vel jelölünk. Így
vagy
ahol 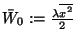 , az új igény érkezésekor
a kiszolgálócsatornában található igény átlagos
hátralévő kiszolgálási ideje. Ezt megkaphatjuk a hátralévő
élettartamra vonatkozó képletünkből, ami
, az új igény érkezésekor
a kiszolgálócsatornában található igény átlagos
hátralévő kiszolgálási ideje. Ezt megkaphatjuk a hátralévő
élettartamra vonatkozó képletünkből, ami
mivel itt 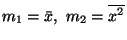 . Viszont ez hátralévő élettartam
esetén teljesül, hiszen élettartamról akkor beszélhetünk,
ha ,,létezik" az a bizonyos dolog, tehát már ,,él". ,,Kiszolgálási
terminológiánk" alapján ezt meg kell még szoroznunk annak
a valószínűségével, hogy van igény a kiszolgálócsatornában,
azaz van értelme hátralévő kiszolgálási időről beszélnünk.
Jelen esetben a rendszer foglaltságának valószínűsége
. Viszont ez hátralévő élettartam
esetén teljesül, hiszen élettartamról akkor beszélhetünk,
ha ,,létezik" az a bizonyos dolog, tehát már ,,él". ,,Kiszolgálási
terminológiánk" alapján ezt meg kell még szoroznunk annak
a valószínűségével, hogy van igény a kiszolgálócsatornában,
azaz van értelme hátralévő kiszolgálási időről beszélnünk.
Jelen esetben a rendszer foglaltságának valószínűsége
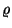 , tehát
, tehát
Ha tekintjük a 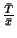 hányadost, ami azt fejezi ki, hogy milyen
,,kényelmetlenséget" okoz a rendszer az igényeknek azzal, hogy
más igényekkel is osztozniuk kell a kiszolgálóegységeken,
a következőt kapjuk:
hányadost, ami azt fejezi ki, hogy milyen
,,kényelmetlenséget" okoz a rendszer az igényeknek azzal, hogy
más igényekkel is osztozniuk kell a kiszolgálóegységeken,
a következőt kapjuk:
és hasonlóan
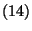 -et valamint
-et valamint 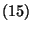 -öt és
-öt és 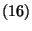 -ot szintén P-H várható érték-formulának
nevezzük.
-ot szintén P-H várható érték-formulának
nevezzük.
![]() a rendszerbe belépő
a rendszerbe belépő ![]() -edik igény;
-edik igény; ![]() a
a ![]() igény beérkezési ideje;
igény beérkezési ideje; ![]()
![]() , a
, a ![]() és
és ![]() igények beérkezése közötti időtartam;
igények beérkezése közötti időtartam; ![]() a
a ![]() igény kiszolgálási ideje;
igény kiszolgálási ideje; ![]() a
a ![]() igény távozásakor hátrahagyott igények
száma;
igény távozásakor hátrahagyott igények
száma; ![]() a
a ![]() igény kiszolgálása alatt a rendszerbe érkező
új igények száma.
igény kiszolgálása alatt a rendszerbe érkező
új igények száma.
![]() az ú.n. beágyazott Markov-lánc, amelynek
egylépéses átmenetvalószínűségei:
az ú.n. beágyazott Markov-lánc, amelynek
egylépéses átmenetvalószínűségei: 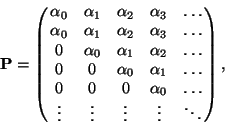
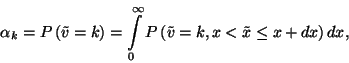
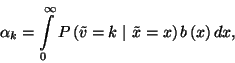
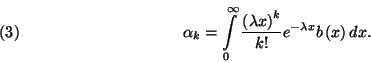
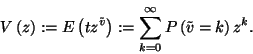
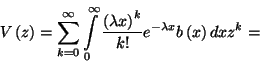
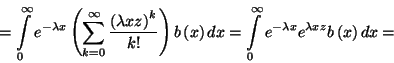
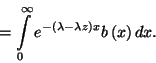
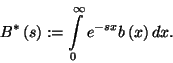
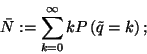

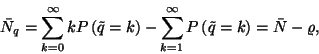
![]() -et valamint
-et valamint ![]() -öt és
-öt és ![]() -ot szintén P-H várható érték-formulának
nevezzük.
-ot szintén P-H várható érték-formulának
nevezzük.