Ebben a szakaszban a
Ebben a szakaszban a ![]() egyenlet további hatványozása
és így a magasabb momentumok meghatározása helyett a
egyenlet további hatványozása
és így a magasabb momentumok meghatározása helyett a ![]() határeloszlását keressük meg. Pontosabban az
eloszlás generátorfüggvényét fogjuk meghatározni.
Hátránya ugyan, hogy ebből néha nehéz meghatározni magát
az eloszlást, viszont igen egyszerűen megkaphatjuk a
határeloszlását keressük meg. Pontosabban az
eloszlás generátorfüggvényét fogjuk meghatározni.
Hátránya ugyan, hogy ebből néha nehéz meghatározni magát
az eloszlást, viszont igen egyszerűen megkaphatjuk a ![]() eloszlásának összes momentumát, ha felhasználjuk
a transzformáltak és deriváltjaik általános tulajdonságait.
Elsőként számoljuk ki annak a valószínűségeloszlásnak
a generátorfüggvényét, hogy hány igény található
a rendszerben közvetlenül egy igény távozása után.
Legyen
eloszlásának összes momentumát, ha felhasználjuk
a transzformáltak és deriváltjaik általános tulajdonságait.
Elsőként számoljuk ki annak a valószínűségeloszlásnak
a generátorfüggvényét, hogy hány igény található
a rendszerben közvetlenül egy igény távozása után.
Legyen
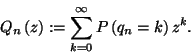
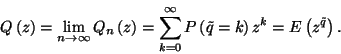
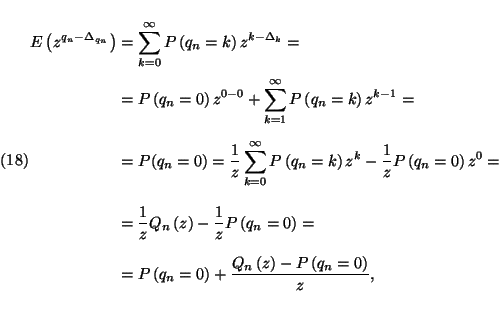
Ezt az egyenletet az első Pollaczek-Hincsin-féle transzformált-egyenletnek nevezzük.
|