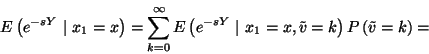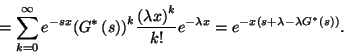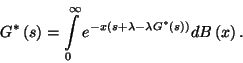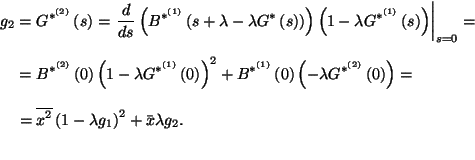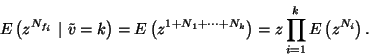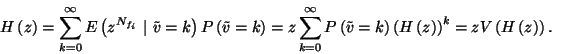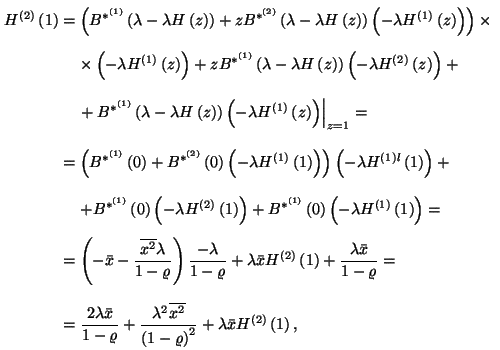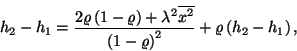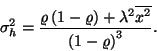III.1.6. A foglaltsági periódusok vizsgálata
Ebben a pontban a sorbanállási rendszereket egy újabb nézőpontból
elemezzük. Vezessük be azt az 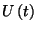 sztochasztikus folyamatot, amely megadja a
sztochasztikus folyamatot, amely megadja a 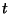 pillanatban a munkahátralékot (restanciát), azaz azt
az időtartamot, amely ahhoz szükséges, hogy a rendszer üressé
váljon, ha a
pillanatban a munkahátralékot (restanciát), azaz azt
az időtartamot, amely ahhoz szükséges, hogy a rendszer üressé
váljon, ha a 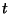 pillanat után új igényt nem engedünk be. Ezt néha
"virtuális" várakozási időnek is nevezzük, mert érkezési
sorrendben történő (FIFO) kiszolgálás esetén megmutatja,
mennyi időt kellene várnia a sorban egy (virtuális) igénynek,
ha a
pillanat után új igényt nem engedünk be. Ezt néha
"virtuális" várakozási időnek is nevezzük, mert érkezési
sorrendben történő (FIFO) kiszolgálás esetén megmutatja,
mennyi időt kellene várnia a sorban egy (virtuális) igénynek,
ha a 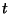 pillanatban lépne be. Mi azonban az általánosabb, munkahátralék
terminológiát fogjuk használni, mivel az bármilyen kiszolgálási
elv esetén érvényes, míg a "virtuális várakozás"
kifejezés csak FIFO elv esetén megfelelő. Ha
pillanatban lépne be. Mi azonban az általánosabb, munkahátralék
terminológiát fogjuk használni, mivel az bármilyen kiszolgálási
elv esetén érvényes, míg a "virtuális várakozás"
kifejezés csak FIFO elv esetén megfelelő. Ha 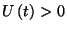 , akkor foglaltnak nevezzük a rendszert,
ha
, akkor foglaltnak nevezzük a rendszert,
ha 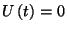 , akkor üresnek. A 2. ábrát tanulmányozva
észrevehetjük, hogy a rendszerben váltakozva jönnek létre
foglalt és szabad időszakok, azaz foglaltsági és üresjárati
intervallumok. A foglaltsági intervallumok hosszát
, akkor üresnek. A 2. ábrát tanulmányozva
észrevehetjük, hogy a rendszerben váltakozva jönnek létre
foglalt és szabad időszakok, azaz foglaltsági és üresjárati
intervallumok. A foglaltsági intervallumok hosszát 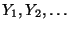 , az üresjárati intervallumokét
, az üresjárati intervallumokét 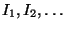 jelöli. Az ábrán a
jelöli. Az ábrán a 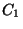 igény a
igény a 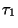 pillanatban lép be a rendszerbe, és
pillanatban lép be a rendszerbe, és  a kiszolgálási ideje. Mivel beérkezése előtt
a rendszer üres volt,
a kiszolgálási ideje. Mivel beérkezése előtt
a rendszer üres volt, 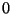 volt a munkahátralék, de a beérkezéssel egy foglaltsági
intervallum kezdődik, és a munkahátralék ezzel
volt a munkahátralék, de a beérkezéssel egy foglaltsági
intervallum kezdődik, és a munkahátralék ezzel  -re ugrik, mivel ennyi ideig tartana, amíg a rendszer újra
üressé válna, ha új beérkezéseket nem engednénk
meg. A
-re ugrik, mivel ennyi ideig tartana, amíg a rendszer újra
üressé válna, ha új beérkezéseket nem engednénk
meg. A 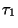 időpont után a munkahátralék egyenletesen --
időpont után a munkahátralék egyenletesen -- 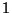 intenzitással -- fogy. A
intenzitással -- fogy. A 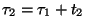 időpontban érkezik a
időpontban érkezik a 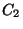 igény a rendszerbe, ezzel a munkahátralék
igény a rendszerbe, ezzel a munkahátralék 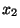 -vel,
-vel, 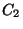 kiszolgálási idejével, függőlegesen felugrik.
Ezután folytatódik a csökkenés, mivel a kiszolgálás
zavartalanul tart. A
kiszolgálási idejével, függőlegesen felugrik.
Ezután folytatódik a csökkenés, mivel a kiszolgálás
zavartalanul tart. A 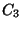 igény
igény 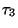 pillanatban érkezik, ez
pillanatban érkezik, ez 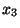 -mal való ugrást eredményez, majd
-mal való ugrást eredményez, majd 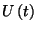 csökkenése folytatódik egészen a
csökkenése folytatódik egészen a
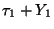 időpillanatig, mikor is az összes rendszerben lévő
igény kiszolgálása befejeződik. Ezzel véget ér a foglaltsági
intervallum és elkezdődik egy új üresjárati intervallum.
időpillanatig, mikor is az összes rendszerben lévő
igény kiszolgálása befejeződik. Ezzel véget ér a foglaltsági
intervallum és elkezdődik egy új üresjárati intervallum.
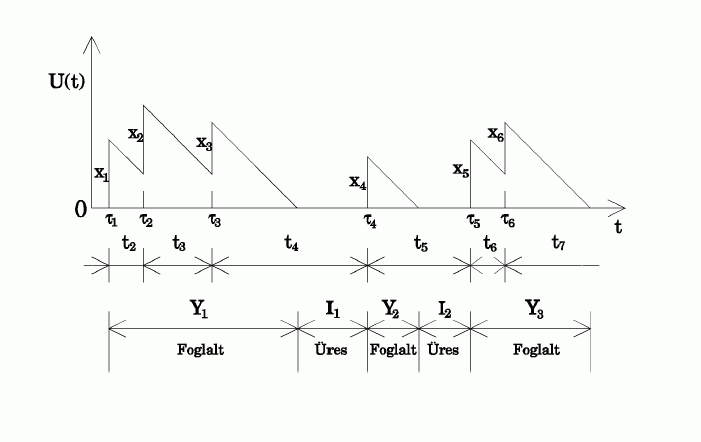
2. ábra
0.6cm Az üresjárat a 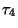 pillanatban ér véget, a
pillanatban ér véget, a 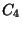 igény beérkezésével. Az általa kezdett
foglaltsági intervallum csak egy igényt tartalmaz. Összefoglalva
az eddigieket, tehát az
igény beérkezésével. Az általa kezdett
foglaltsági intervallum csak egy igényt tartalmaz. Összefoglalva
az eddigieket, tehát az 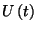 függvénynek függőleges (pozitív)
ugrása van minden igénybeérkezéskor, aminek nagysága
éppen az adott igény kiszolgálási ideje. Ezután lineárisan
(
függvénynek függőleges (pozitív)
ugrása van minden igénybeérkezéskor, aminek nagysága
éppen az adott igény kiszolgálási ideje. Ezután lineárisan
(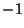 iránytangenssel) csökken, egészen addig, míg
iránytangenssel) csökken, egészen addig, míg
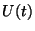 pozitív. Ha elérte a nulla értéket, akkor nulla
marad a következő igény beérkezéséig. Ez a sztochasztikus
folyamat folytonos állapotterű, diszkrét ugrásokat tartalmazó
Markov folyamat, hiszen a hátralévő munkát jelenti, ami a múlttal
a jelenen keresztül van csak kapcsolatban. Vegyük még észre,
hogy ha a kiszolgálási elv FIFO, akkor az ábrán a távozási
pillanatokat az
pozitív. Ha elérte a nulla értéket, akkor nulla
marad a következő igény beérkezéséig. Ez a sztochasztikus
folyamat folytonos állapotterű, diszkrét ugrásokat tartalmazó
Markov folyamat, hiszen a hátralévő munkát jelenti, ami a múlttal
a jelenen keresztül van csak kapcsolatban. Vegyük még észre,
hogy ha a kiszolgálási elv FIFO, akkor az ábrán a távozási
pillanatokat az 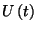 függvénygörbe csökkenő szakaszainak
a vízszintes tengelyig történő meghosszabbításával
kaphatjuk meg. Az
függvénygörbe csökkenő szakaszainak
a vízszintes tengelyig történő meghosszabbításával
kaphatjuk meg. Az 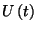 függény értéke független
a kiszolgálási elvtől, csak azt használjuk fel, hogy a kiszolgálóegység
foglalt, amíg igény van a rendszerben, és minden igény csak
a teljes kiszolgálása után távozzon a rendszerből. Az ilyen
rendszert munkamegőrzëëő rendszernek nevezzük. Nézzük
most meg közelebbről az üresjárati és foglaltsági intervallumok
eloszlását. Feltevésünk szerint (
függény értéke független
a kiszolgálási elvtől, csak azt használjuk fel, hogy a kiszolgálóegység
foglalt, amíg igény van a rendszerben, és minden igény csak
a teljes kiszolgálása után távozzon a rendszerből. Az ilyen
rendszert munkamegőrzëëő rendszernek nevezzük. Nézzük
most meg közelebbről az üresjárati és foglaltsági intervallumok
eloszlását. Feltevésünk szerint (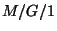 rendszerben)
rendszerben)
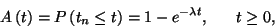
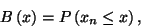
ahol 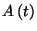 és
és  is független
is független 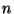 -től. A minket érdeklő eloszlások
-től. A minket érdeklő eloszlások
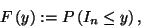
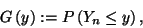
az üresjárati és a foglaltsági intervallum eloszülásai.
Kezdjük az üresjárati intervallumok eloszlásával, amit
az 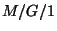 rendszer esetén elég egyszerű meghatározni. Amikor
egy foglaltsági intervallum véget ér, akkor ezzel együtt elkezdődik
egy üresjárati intervallum, és ez befejeződik, amint egy új
igény érkezik. A Markovitás miatt az új igény beérkezéséig
tartó idő
rendszer esetén elég egyszerű meghatározni. Amikor
egy foglaltsági intervallum véget ér, akkor ezzel együtt elkezdődik
egy üresjárati intervallum, és ez befejeződik, amint egy új
igény érkezik. A Markovitás miatt az új igény beérkezéséig
tartó idő 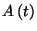 eloszlású, így
eloszlású, így
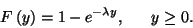
A foglaltsági intervallumok eloszlását már kissé bonyolultabb
meghatározni. A 3. ábra az  munkahátralékot ábrázolja. A
munkahátralékot ábrázolja. A  pillanatban érkezik az addig üres rendszerbe a
pillanatban érkezik az addig üres rendszerbe a  igény, melynek kiszolgálási ideje
igény, melynek kiszolgálási ideje  , így
, így 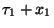 a távozási időpontja.
a távozási időpontja. 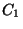 kiszolgálása alatt új igények léphetnek
be a rendszerbe, melyekkel folytatódik a foglaltsági intervallum.
A könnyebb kezelhetőség érdekében részekre bontjuk
a
kiszolgálása alatt új igények léphetnek
be a rendszerbe, melyekkel folytatódik a foglaltsági intervallum.
A könnyebb kezelhetőség érdekében részekre bontjuk
a 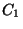 által generált foglaltsági intervallumot. A Takács
Lajos által használt módszert alkalmazzuk, nevezetesen a FIFO
kiszolgálási elv helyett LIFO-t használunk, azaz az utolsónak
érkezett igényt szolgáljuk ki először. Ezt megtehetjük,
hiszen tudjuk, hogy a foglaltsági intervallum hosszának eloszlása
független az igények kiszolgálási sorrendjétől.
Így tehát
által generált foglaltsági intervallumot. A Takács
Lajos által használt módszert alkalmazzuk, nevezetesen a FIFO
kiszolgálási elv helyett LIFO-t használunk, azaz az utolsónak
érkezett igényt szolgáljuk ki először. Ezt megtehetjük,
hiszen tudjuk, hogy a foglaltsági intervallum hosszának eloszlása
független az igények kiszolgálási sorrendjétől.
Így tehát 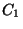 távozásakor a
távozásakor a 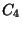 kerül a kiszolgálócsatornába,
kerül a kiszolgálócsatornába, 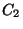 -t és
-t és 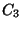 -at időlegesen úgy tekintjük, mintha nem lennének
a rendszerben. Emiatt a
-at időlegesen úgy tekintjük, mintha nem lennének
a rendszerben. Emiatt a 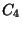 kiszolgálásának kezdőpillanatát úgy tekinthetjük,
mintha új foglaltsági intervallum -- tulajdonképpen foglaltsági
részintervallum -- kezdődne. Ennek a részintervallumnak a hossza
kiszolgálásának kezdőpillanatát úgy tekinthetjük,
mintha új foglaltsági intervallum -- tulajdonképpen foglaltsági
részintervallum -- kezdődne. Ennek a részintervallumnak a hossza
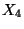 , az az idő, amíg a
, az az idő, amíg a 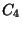 -nek és a
-nek és a 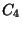 kiszolgálása alatt beérkezett igényeknek a kiszolgálása
tart. Példánkban az
kiszolgálása alatt beérkezett igényeknek a kiszolgálása
tart. Példánkban az 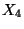 intervallum alatt a
intervallum alatt a 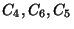 igényeket szolgálják ki.
igényeket szolgálják ki. 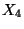 végén, a
végén, a 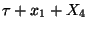 pillanatban a LIFO elv szerint -- folytatva a rekurziót
-- a
pillanatban a LIFO elv szerint -- folytatva a rekurziót
-- a 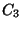 igény kiszolgálása kezdődik el. Az általa generált
foglaltsági részintervallum hosszúsága
igény kiszolgálása kezdődik el. Az általa generált
foglaltsági részintervallum hosszúsága 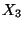 , ami alatt a
, ami alatt a 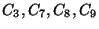 igények kerülnek kiszolgálásra.
Ennek végeztével a
igények kerülnek kiszolgálásra.
Ennek végeztével a 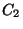 igény kerül sorra az előzőekhez hasonlóan, és
utána véget is ér a
igény kerül sorra az előzőekhez hasonlóan, és
utána véget is ér a 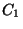 által generált foglaltsági intervallum.
által generált foglaltsági intervallum.
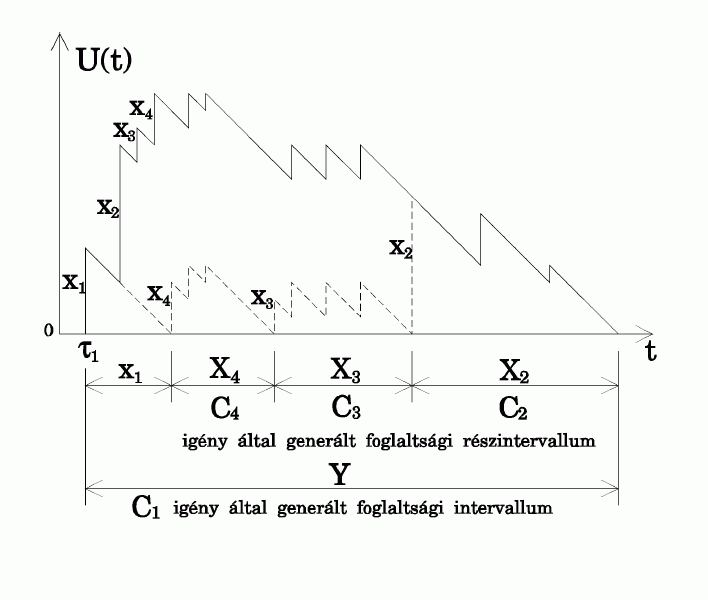
3. ábra
A foglaltsági intervallum
A 3. ábrán látszik, hogy egy foglaltsági részintervallum
grafikonja megegyezik a foglaltsági intervallum grafikonjával, egy konstanssal
eltolva, ami éppen azon igények kiszolgálási idejének
összegével egyezik meg, amelyek 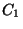 kiszolgálása alatt érkeztek, és még nem
volt lehetőségük a saját foglaltsági részintervallumuk
generálására. Vegyük észre, hogy a foglaltsági részintervallumok
statisztikusan éppen úgy viselkednek, mint a teljes foglaltsági
intervallum, hiszen az összes részintervallumot is egy-egy igény
nyitja meg, ezek kiszolgálási ideje azonos eloszlású és
egymástól függetlenek, valamint minden részintervallum addig
tart, amíg a rendszer be nem pótol<ja az elmaradt munkát, azaz
az
kiszolgálása alatt érkeztek, és még nem
volt lehetőségük a saját foglaltsági részintervallumuk
generálására. Vegyük észre, hogy a foglaltsági részintervallumok
statisztikusan éppen úgy viselkednek, mint a teljes foglaltsági
intervallum, hiszen az összes részintervallumot is egy-egy igény
nyitja meg, ezek kiszolgálási ideje azonos eloszlású és
egymástól függetlenek, valamint minden részintervallum addig
tart, amíg a rendszer be nem pótol<ja az elmaradt munkát, azaz
az 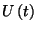 nullává nem válik. Tehát az
nullává nem válik. Tehát az 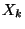 valószínűségi változók független,
azonos eloszlásúak és eloszlásuk megegyezik
valószínűségi változók független,
azonos eloszlásúak és eloszlásuk megegyezik 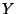 eloszlásával. Ezek miatt felírhatjuk, hogy az
eloszlásával. Ezek miatt felírhatjuk, hogy az 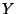 hosszúságú foglaltsági intervallum
hosszúságú foglaltsági intervallum 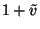 számú valószínűségi változó
összegével egyenlő, ahol a
számú valószínűségi változó
összegével egyenlő, ahol a 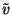 valószínűségi változó a
valószínűségi változó a 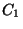 kiszolgálása alatt beérkezett igények számával
egyenlő. Az első a
kiszolgálása alatt beérkezett igények számával
egyenlő. Az első a 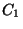 kiszolgálási ideje, a többi a foglaltsági részintervallumok
hossza, melyek eloszlása azonos
kiszolgálási ideje, a többi a foglaltsági részintervallumok
hossza, melyek eloszlása azonos 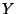 eloszlásával. Így
eloszlásával. Így
Tudjuk, hogy 
 eloszlású és
eloszlású és 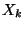
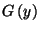 eloszlású. Intuitíven érezhető,
hogy a foglaltsági intervallumok eloszlása és a kiszolgálási
idő eloszlása kapcsolatban állnak egymással. Hogy többet megtudjunk
erről, számoljuk ki a következő feltételes transzformáltakat:
eloszlású. Intuitíven érezhető,
hogy a foglaltsági intervallumok eloszlása és a kiszolgálási
idő eloszlása kapcsolatban állnak egymással. Hogy többet megtudjunk
erről, számoljuk ki a következő feltételes transzformáltakat:
A foglaltsági részintervallumok időtartamai egymástól függetlenek,
ezért
Mivel 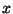 állandó, így
állandó, így 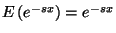 , és mert a foglaltsági részintervallumok
azonos eloszlásúak, melynek Laplace-Stieltjes transzformáltja
, és mert a foglaltsági részintervallumok
azonos eloszlásúak, melynek Laplace-Stieltjes transzformáltja 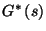 , ezért
, ezért
Mivel 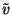 az
az 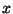 hosszúságú intervallum alatti beérkezések
számát jelenti, ezért
hosszúságú intervallum alatti beérkezések
számát jelenti, ezért 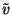 Poisson-eloszlású, várható értéke
Poisson-eloszlású, várható értéke
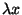 . Tüntessük el a
. Tüntessük el a 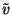 szerinti feltételt:
szerinti feltételt:
Az  szerinti feltételt
szerinti feltételt  szerinti integrálással küszöböljük
ki, így azt kapjuk, hogy
szerinti integrálással küszöböljük
ki, így azt kapjuk, hogy
Ez éppen a kiszolgálási idő sűrűségfüggvényének
Laplace-transzformáltja az 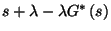 helyen, azaz
helyen, azaz
Ezt a függvényegyenletet általában nem lehet invertálni,
viszont numerikusan megoldható tetszőleges 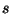 értékre a következő iterációval:
értékre a következő iterációval:
ha 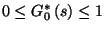 . Ha
. Ha 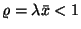 , akkor az eljárással a
, akkor az eljárással a 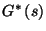 -et kapjuk meg, így megkísérelhetjük
a kapott értékek numerikus inverzióját. (Lásd Kleinrock
(1979)) (23) alapján a foglaltsági intervallumok eloszlásának
momentumait is meg tudjuk határozni. Legyen
-et kapjuk meg, így megkísérelhetjük
a kapott értékek numerikus inverzióját. (Lásd Kleinrock
(1979)) (23) alapján a foglaltsági intervallumok eloszlásának
momentumait is meg tudjuk határozni. Legyen
akkor 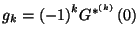 és
és
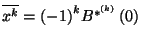 ,
,
ahol felhasználtuk, hogy ha 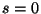 , akkor
, akkor 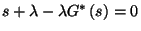 . Így
. Így
Mivel 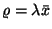 , a következőt kapjuk:
, a következőt kapjuk:
Két dolgot vegyünk észre. Egyrészt, hogy ez csak 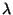 és
és 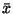 függvénye, másrészt, összehasonlítva
ezt az ismert
függvénye, másrészt, összehasonlítva
ezt az ismert 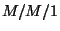 rendszer paramétereivel, azt tapasztaljuk, hogy az
rendszer paramétereivel, azt tapasztaljuk, hogy az 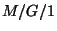 -beli foglaltsági intervallumok hosszának várható
értéke azonosan számolható az
-beli foglaltsági intervallumok hosszának várható
értéke azonosan számolható az 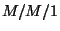 -ben az igények rendszerben eltöltött átlagos
tartózkodási idejével.
-ben az igények rendszerben eltöltött átlagos
tartózkodási idejével.
A második momentumhoz használjuk
fel az ismert összefüggéseket.
Innen
azaz
Ha tovább számolunk, megfigyelhetjük, hogy a magasabb momentumok
nevezőjében az 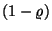 kitevője nő, és ez a meghatározó
a momentumok viselkedésében, ha
kitevője nő, és ez a meghatározó
a momentumok viselkedésében, ha 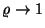 . Számoljuk ki még a foglaltsági intervallum
hosszának szórásnégyzetét:
. Számoljuk ki még a foglaltsági intervallum
hosszának szórásnégyzetét:
adódik, ahol 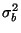 a kiszolgálási idő eloszlásának szórásnégyzete.
Legyen
a kiszolgálási idő eloszlásának szórásnégyzete.
Legyen 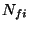 a foglaltsági intervallum alatt kiszolgált igények
száma. Vizsgáljuk meg most ennek az eloszlását,
a foglaltsági intervallum alatt kiszolgált igények
száma. Vizsgáljuk meg most ennek az eloszlását,
Ezen diszkrét eloszlás generátorfüggvénye legyen
Az 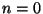 tag azért hiányzik, mert egy foglaltsági intervallum
alatt legalább egy igényt ki kell szolgálni. Láttuk, hogy
a
tag azért hiányzik, mert egy foglaltsági intervallum
alatt legalább egy igényt ki kell szolgálni. Láttuk, hogy
a 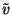 valószínűségi változó jelenti az
egy igény kiszolgálási ideje alatt a rendszerbe érkező igények
számát, és ennek
valószínűségi változó jelenti az
egy igény kiszolgálási ideje alatt a rendszerbe érkező igények
számát, és ennek 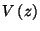 generátorfüggvényére levezettük
a (8) relációt, azaz
generátorfüggvényére levezettük
a (8) relációt, azaz
egyenletet. A foglaltsági intervallum hossza meghatározásához
hasonlóan most képezzük a 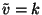 feltételek melletti feltételes valószínűségeket.
Ezek mindegyike egy foglaltsági részintervallumot generál, és
az ezekben kiszolgált igények számának eloszlása szintén
feltételek melletti feltételes valószínűségeket.
Ezek mindegyike egy foglaltsági részintervallumot generál, és
az ezekben kiszolgált igények számának eloszlása szintén
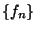 . Jelölje
. Jelölje 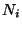 az
az 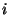 -edik foglaltsági részintervallum alatt kiszolgált igények
számát. Ebből
-edik foglaltsági részintervallum alatt kiszolgált igények
számát. Ebből
mivel az 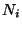 -k független, azonos eloszlásúak. Mivel minden
-k független, azonos eloszlásúak. Mivel minden 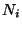 eloszlása ugyanaz, mint
eloszlása ugyanaz, mint 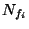 eloszlása, ezért
eloszlása, ezért
Ennek a felhasználásával a feltételes várható érték
tétele alapján
Végül (8)< szerint felírhatjuk, hogy
Ez meglehetősen hasonlít a foglaltsági intervallum hosszának eloszlásánál
kapott eredményre. Könnyen kiszámolhatjuk belőle a foglaltsági
intervallumok alatt kiszolgált igények számának 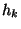 momentumait. A Laplace-transzformált és a generátorfüggvény
tulajdonságai miatt
momentumait. A Laplace-transzformált és a generátorfüggvény
tulajdonságai miatt
mivel 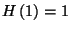 . Tehát
. Tehát
azaz
Továbbá
azaz
A kiszolgált igények szórásnégyzete:
azaz
![]() sztochasztikus folyamatot, amely megadja a
sztochasztikus folyamatot, amely megadja a ![]() pillanatban a munkahátralékot (restanciát), azaz azt
az időtartamot, amely ahhoz szükséges, hogy a rendszer üressé
váljon, ha a
pillanatban a munkahátralékot (restanciát), azaz azt
az időtartamot, amely ahhoz szükséges, hogy a rendszer üressé
váljon, ha a ![]() pillanat után új igényt nem engedünk be. Ezt néha
"virtuális" várakozási időnek is nevezzük, mert érkezési
sorrendben történő (FIFO) kiszolgálás esetén megmutatja,
mennyi időt kellene várnia a sorban egy (virtuális) igénynek,
ha a
pillanat után új igényt nem engedünk be. Ezt néha
"virtuális" várakozási időnek is nevezzük, mert érkezési
sorrendben történő (FIFO) kiszolgálás esetén megmutatja,
mennyi időt kellene várnia a sorban egy (virtuális) igénynek,
ha a ![]() pillanatban lépne be. Mi azonban az általánosabb, munkahátralék
terminológiát fogjuk használni, mivel az bármilyen kiszolgálási
elv esetén érvényes, míg a "virtuális várakozás"
kifejezés csak FIFO elv esetén megfelelő. Ha
pillanatban lépne be. Mi azonban az általánosabb, munkahátralék
terminológiát fogjuk használni, mivel az bármilyen kiszolgálási
elv esetén érvényes, míg a "virtuális várakozás"
kifejezés csak FIFO elv esetén megfelelő. Ha ![]() , akkor foglaltnak nevezzük a rendszert,
ha
, akkor foglaltnak nevezzük a rendszert,
ha ![]() , akkor üresnek. A 2. ábrát tanulmányozva
észrevehetjük, hogy a rendszerben váltakozva jönnek létre
foglalt és szabad időszakok, azaz foglaltsági és üresjárati
intervallumok. A foglaltsági intervallumok hosszát
, akkor üresnek. A 2. ábrát tanulmányozva
észrevehetjük, hogy a rendszerben váltakozva jönnek létre
foglalt és szabad időszakok, azaz foglaltsági és üresjárati
intervallumok. A foglaltsági intervallumok hosszát ![]() , az üresjárati intervallumokét
, az üresjárati intervallumokét ![]() jelöli. Az ábrán a
jelöli. Az ábrán a ![]() igény a
igény a ![]() pillanatban lép be a rendszerbe, és
pillanatban lép be a rendszerbe, és ![]() a kiszolgálási ideje. Mivel beérkezése előtt
a rendszer üres volt,
a kiszolgálási ideje. Mivel beérkezése előtt
a rendszer üres volt, ![]() volt a munkahátralék, de a beérkezéssel egy foglaltsági
intervallum kezdődik, és a munkahátralék ezzel
volt a munkahátralék, de a beérkezéssel egy foglaltsági
intervallum kezdődik, és a munkahátralék ezzel ![]() -re ugrik, mivel ennyi ideig tartana, amíg a rendszer újra
üressé válna, ha új beérkezéseket nem engednénk
meg. A
-re ugrik, mivel ennyi ideig tartana, amíg a rendszer újra
üressé válna, ha új beérkezéseket nem engednénk
meg. A ![]() időpont után a munkahátralék egyenletesen --
időpont után a munkahátralék egyenletesen -- ![]() intenzitással -- fogy. A
intenzitással -- fogy. A ![]() időpontban érkezik a
időpontban érkezik a ![]() igény a rendszerbe, ezzel a munkahátralék
igény a rendszerbe, ezzel a munkahátralék ![]() -vel,
-vel, ![]() kiszolgálási idejével, függőlegesen felugrik.
Ezután folytatódik a csökkenés, mivel a kiszolgálás
zavartalanul tart. A
kiszolgálási idejével, függőlegesen felugrik.
Ezután folytatódik a csökkenés, mivel a kiszolgálás
zavartalanul tart. A ![]() igény
igény ![]() pillanatban érkezik, ez
pillanatban érkezik, ez ![]() -mal való ugrást eredményez, majd
-mal való ugrást eredményez, majd ![]() csökkenése folytatódik egészen a
csökkenése folytatódik egészen a
![]() időpillanatig, mikor is az összes rendszerben lévő
igény kiszolgálása befejeződik. Ezzel véget ér a foglaltsági
intervallum és elkezdődik egy új üresjárati intervallum.
időpillanatig, mikor is az összes rendszerben lévő
igény kiszolgálása befejeződik. Ezzel véget ér a foglaltsági
intervallum és elkezdődik egy új üresjárati intervallum.

![]() munkahátralékot ábrázolja. A
munkahátralékot ábrázolja. A ![]() pillanatban érkezik az addig üres rendszerbe a
pillanatban érkezik az addig üres rendszerbe a ![]() igény, melynek kiszolgálási ideje
igény, melynek kiszolgálási ideje ![]() , így
, így ![]() a távozási időpontja.
a távozási időpontja. ![]() kiszolgálása alatt új igények léphetnek
be a rendszerbe, melyekkel folytatódik a foglaltsági intervallum.
A könnyebb kezelhetőség érdekében részekre bontjuk
a
kiszolgálása alatt új igények léphetnek
be a rendszerbe, melyekkel folytatódik a foglaltsági intervallum.
A könnyebb kezelhetőség érdekében részekre bontjuk
a ![]() által generált foglaltsági intervallumot. A Takács
Lajos által használt módszert alkalmazzuk, nevezetesen a FIFO
kiszolgálási elv helyett LIFO-t használunk, azaz az utolsónak
érkezett igényt szolgáljuk ki először. Ezt megtehetjük,
hiszen tudjuk, hogy a foglaltsági intervallum hosszának eloszlása
független az igények kiszolgálási sorrendjétől.
Így tehát
által generált foglaltsági intervallumot. A Takács
Lajos által használt módszert alkalmazzuk, nevezetesen a FIFO
kiszolgálási elv helyett LIFO-t használunk, azaz az utolsónak
érkezett igényt szolgáljuk ki először. Ezt megtehetjük,
hiszen tudjuk, hogy a foglaltsági intervallum hosszának eloszlása
független az igények kiszolgálási sorrendjétől.
Így tehát ![]() távozásakor a
távozásakor a ![]() kerül a kiszolgálócsatornába,
kerül a kiszolgálócsatornába, ![]() -t és
-t és ![]() -at időlegesen úgy tekintjük, mintha nem lennének
a rendszerben. Emiatt a
-at időlegesen úgy tekintjük, mintha nem lennének
a rendszerben. Emiatt a ![]() kiszolgálásának kezdőpillanatát úgy tekinthetjük,
mintha új foglaltsági intervallum -- tulajdonképpen foglaltsági
részintervallum -- kezdődne. Ennek a részintervallumnak a hossza
kiszolgálásának kezdőpillanatát úgy tekinthetjük,
mintha új foglaltsági intervallum -- tulajdonképpen foglaltsági
részintervallum -- kezdődne. Ennek a részintervallumnak a hossza
![]() , az az idő, amíg a
, az az idő, amíg a ![]() -nek és a
-nek és a ![]() kiszolgálása alatt beérkezett igényeknek a kiszolgálása
tart. Példánkban az
kiszolgálása alatt beérkezett igényeknek a kiszolgálása
tart. Példánkban az ![]() intervallum alatt a
intervallum alatt a ![]() igényeket szolgálják ki.
igényeket szolgálják ki. ![]() végén, a
végén, a ![]() pillanatban a LIFO elv szerint -- folytatva a rekurziót
-- a
pillanatban a LIFO elv szerint -- folytatva a rekurziót
-- a ![]() igény kiszolgálása kezdődik el. Az általa generált
foglaltsági részintervallum hosszúsága
igény kiszolgálása kezdődik el. Az általa generált
foglaltsági részintervallum hosszúsága ![]() , ami alatt a
, ami alatt a ![]() igények kerülnek kiszolgálásra.
Ennek végeztével a
igények kerülnek kiszolgálásra.
Ennek végeztével a ![]() igény kerül sorra az előzőekhez hasonlóan, és
utána véget is ér a
igény kerül sorra az előzőekhez hasonlóan, és
utána véget is ér a ![]() által generált foglaltsági intervallum.
által generált foglaltsági intervallum.