III.1.7. A Takács-féle integrodifferenciál-egyenlet
Ebben a fejezetben az 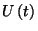 munkahátralékot vizsgáljuk meg kissé
közelebbről. Korábban megállapítottuk, hogy az
munkahátralékot vizsgáljuk meg kissé
közelebbről. Korábban megállapítottuk, hogy az 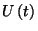 folytonos idejű, folytonos állapotterű, az igények
beérkezési pillanataiban diszkrét ugrásokat tartalmazó
Markov-folyamat. Most az
folytonos idejű, folytonos állapotterű, az igények
beérkezési pillanataiban diszkrét ugrásokat tartalmazó
Markov-folyamat. Most az 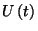 eloszlásfüggvényére vezetünk
le egy összefüggést, a
eloszlásfüggvényére vezetünk
le egy összefüggést, a 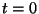 pillanatban adott kezdeti érték mellett. Legyen
pillanatban adott kezdeti érték mellett. Legyen
azaz annak a valószínűsége, hogy a 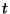 időpontban érkező ,,virtuális" igény
időpontban érkező ,,virtuális" igény 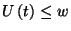 ideig tartózkodik a rendszerben, ha tudjuk,
hogy
ideig tartózkodik a rendszerben, ha tudjuk,
hogy 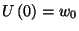 .
. 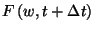 -re szeretnénk egy kifejezést kapni
-re szeretnénk egy kifejezést kapni
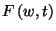 és
és 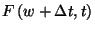 segítségével. Az
segítségével. Az 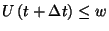 esemény a
esemény a 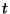 pillanatbeli állapotból úgy valósulhat meg, ha
pillanatbeli állapotból úgy valósulhat meg, ha
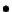 vagy a
vagy a 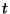 pillanatban a munkahátralék nem nagyobb
pillanatban a munkahátralék nem nagyobb 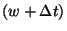 -nél és nem érkezik igény
a
-nél és nem érkezik igény
a 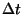 időközben, aminek a valószínűsége az elemi
sorbanállási elméletből jól ismert:
időközben, aminek a valószínűsége az elemi
sorbanállási elméletből jól ismert:  ;
;
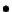 vagy egyetlen beérkezés fordul elő a
vagy egyetlen beérkezés fordul elő a 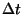 intervallumban -- ennek valószínűsége
intervallumban -- ennek valószínűsége 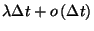 -- úgy, hogy az ez által
hozott munka és a
-- úgy, hogy az ez által
hozott munka és a 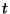 pillanatbeli munkahátralék összege nem haladja meg
pillanatbeli munkahátralék összege nem haladja meg
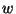 -t. Az
-t. Az 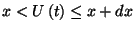 valószínűségét így
írhatjuk fel:
valószínűségét így
írhatjuk fel:
Annak a valószínűsége pedig, hogy a kiszolgálási idő
nem nagyobb, mint 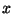 , éppen
, éppen 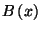 . Mivel egy igény kiszolgálási ideje független
a munkahátraléktól, annak a valószínűsége, hogy
az új igény munkaszükségletével együtt sem haladja
meg az
. Mivel egy igény kiszolgálási ideje független
a munkahátraléktól, annak a valószínűsége, hogy
az új igény munkaszükségletével együtt sem haladja
meg az 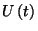 a
a 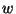 -t, szorzatként írható
-t, szorzatként írható
alakban. A teljes valószínűség tétele alapján felírhatjuk,
hogy
Az eloszlásfüggvényt az első változója szerint sorbafejtve
(csak a lineáris tagot véve)
Használjuk ezt fel 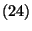 -ben:
-ben:
Ezen egyenletnek ki kell elégítenie a következő feltételeket:
Most mindkét oldalból vonjunk ki 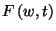 -t, osszunk
-t, osszunk 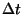 -vel és képezzük a
-vel és képezzük a 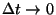 határátmenetet. Így kapjuk az
határátmenetet. Így kapjuk az 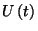 eloszlásfüggvényére vonatkozó
Takács-féle integrodifferenciál-egyenletet:
eloszlásfüggvényére vonatkozó
Takács-féle integrodifferenciál-egyenletet:
Takács ezt az összefüggést inhomogén Poisson-folyamatra
( 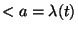 ) is levezette. Ekkor majdnem minden
) is levezette. Ekkor majdnem minden 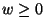 és
és 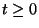 -ra fennáll az egyenlet.*Csak azon
-ra fennáll az egyenlet.*Csak azon 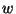 és
és 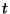 értékekre nem áll fenn, melyekre
értékekre nem áll fenn, melyekre 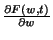 nem létezik, például
nem létezik, például
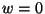 -ban. A Takács-féle integrodifferenciál-egyenletből
több információt is levezethetünk. Vegyük a
-ban. A Takács-féle integrodifferenciál-egyenletből
több információt is levezethetünk. Vegyük a 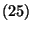 -nek az első változóX,
-nek az első változóX, 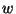 szerinti Laplace- Stieltjes transzformáltját:
szerinti Laplace- Stieltjes transzformáltját:
A Függelék alapján
és hasonlóan
Mivel a munkahátralék és a kiszolgálási idő nemnegatív
valószínűségi változók, 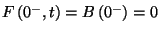 . Az integrodifferenciál-egyenlet
integrált tartalmazó tagjában a
. Az integrodifferenciál-egyenlet
integrált tartalmazó tagjában a 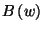 és
és 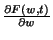 konvolúciója szerepel,
ennek a transzformáltja pedig a transzformáltak szorzata. Még a
konvolúciója szerepel,
ennek a transzformáltja pedig a transzformáltak szorzata. Még a
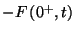 tag szorul magyarázatra. A
tag szorul magyarázatra. A 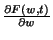 transzformáltja
transzformáltja 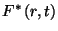 , de ez magában foglalja az
, de ez magában foglalja az 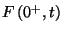 tagot is, viszont a Takács-féle integrodifferenciál-egyenlet
ezt nem tartalmazza (
tagot is, viszont a Takács-féle integrodifferenciál-egyenlet
ezt nem tartalmazza (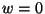 -ra nincs értelme), ezért kivonjuk
-ra nincs értelme), ezért kivonjuk 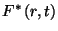 -ből. Ezek alapján kaptuk tehát a
-ből. Ezek alapján kaptuk tehát a 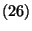 -ot. Ha az
-ot. Ha az 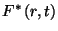 -t a második változó szerint is transzformáljuk,
a következőképpen számolunk. Az
-t a második változó szerint is transzformáljuk,
a következőképpen számolunk. Az
definíciót felhasználva a 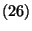 -ból és a derivált Laplace-transzformáltjára
vonatkozó összefüggésből
-ból és a derivált Laplace-transzformáltjára
vonatkozó összefüggésből
ha az
definíciót használjuk az utolsó tagban. Innen
Ezen függvények stacionárius megoldását is megvizsgáljuk.
Meg lehet mutatni, hogy az 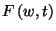 -nek
-nek 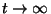 esetén létezik az
esetén létezik az 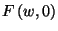 kezdeti értéktől független határfüggvénye,
ha
kezdeti értéktől független határfüggvénye,
ha 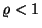 , legyen
, legyen 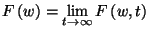 . A Takács-féle
integrodifferenciál-egyenletből a bal oldal
. A Takács-féle
integrodifferenciál-egyenletből a bal oldal 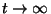 esetén nullához tart, így
esetén nullához tart, így
Továbbá ha 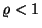 , akkor
, akkor 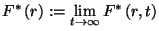 is létezik
és független a kezdeti eloszlástól. Tekintsük a
is létezik
és független a kezdeti eloszlástól. Tekintsük a 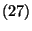 Laplace-Stieltjes transzformáltját, és
a
Laplace-Stieltjes transzformáltját, és
a 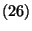 levezetéséhez hasonlóan kapjuk, hogy
levezetéséhez hasonlóan kapjuk, hogy
ahol 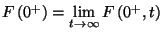 , azaz
annak a valószínűsége, hogy a munkahátralék mennyisége
nulla. Ezután
, azaz
annak a valószínűsége, hogy a munkahátralék mennyisége
nulla. Ezután
Tudjuk, hogy 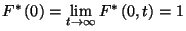 , ebből
a L'Hospital szabályt használva
, ebből
a L'Hospital szabályt használva
azaz 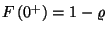 , annak a valószínűsége, hogy
a rendszer szabad, ami összhangban van az
, annak a valószínűsége, hogy
a rendszer szabad, ami összhangban van az 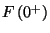 -ra tett korábbi megállapításainkkal.
Végül adódik, hogy
-ra tett korábbi megállapításainkkal.
Végül adódik, hogy
Emlékezzünk vissza a várakozási időre vonatkozó P-H transzformált
egyenletre
Így 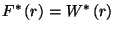 , azaz stacionárius esetben
a hátralévő kiszolgálási idő sűrűségfüggvényének
és a várakozási idő sűrűségfüggvényének Laplace-transzformáltja
megegyezik.
, azaz stacionárius esetben
a hátralévő kiszolgálási idő sűrűségfüggvényének
és a várakozási idő sűrűségfüggvényének Laplace-transzformáltja
megegyezik.
![]() munkahátralékot vizsgáljuk meg kissé
közelebbről. Korábban megállapítottuk, hogy az
munkahátralékot vizsgáljuk meg kissé
közelebbről. Korábban megállapítottuk, hogy az ![]() folytonos idejű, folytonos állapotterű, az igények
beérkezési pillanataiban diszkrét ugrásokat tartalmazó
Markov-folyamat. Most az
folytonos idejű, folytonos állapotterű, az igények
beérkezési pillanataiban diszkrét ugrásokat tartalmazó
Markov-folyamat. Most az ![]() eloszlásfüggvényére vezetünk
le egy összefüggést, a
eloszlásfüggvényére vezetünk
le egy összefüggést, a ![]() pillanatban adott kezdeti érték mellett. Legyen
pillanatban adott kezdeti érték mellett. Legyen ![]() vagy a
vagy a ![]() pillanatban a munkahátralék nem nagyobb
pillanatban a munkahátralék nem nagyobb ![]() -nél és nem érkezik igény
a
-nél és nem érkezik igény
a ![]() időközben, aminek a valószínűsége az elemi
sorbanállási elméletből jól ismert:
időközben, aminek a valószínűsége az elemi
sorbanállási elméletből jól ismert: ![]() ;
; ![]() vagy egyetlen beérkezés fordul elő a
vagy egyetlen beérkezés fordul elő a ![]() intervallumban -- ennek valószínűsége
intervallumban -- ennek valószínűsége ![]() -- úgy, hogy az ez által
hozott munka és a
-- úgy, hogy az ez által
hozott munka és a ![]() pillanatbeli munkahátralék összege nem haladja meg
pillanatbeli munkahátralék összege nem haladja meg
![]() -t. Az
-t. Az ![]() valószínűségét így
írhatjuk fel:
valószínűségét így
írhatjuk fel: 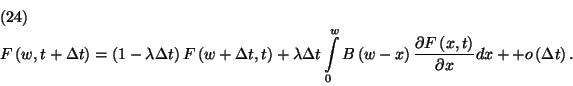
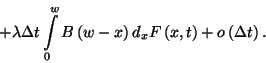
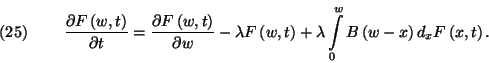
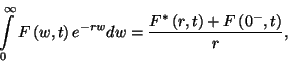
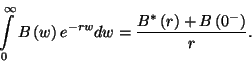
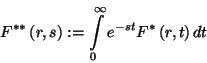
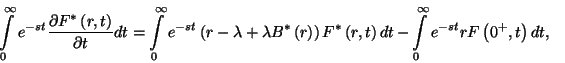
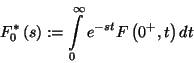
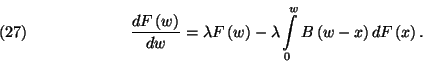
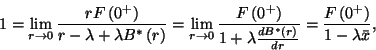
![]() , azaz stacionárius esetben
a hátralévő kiszolgálási idő sűrűségfüggvényének
és a várakozási idő sűrűségfüggvényének Laplace-transzformáltja
megegyezik.
, azaz stacionárius esetben
a hátralévő kiszolgálási idő sűrűségfüggvényének
és a várakozási idő sűrűségfüggvényének Laplace-transzformáltja
megegyezik.