III.3. Az <n/M/G/1/PS> rendszer


Egy olyan számítógépes rendszert tekintünk, amely egy központi egységből és $n$ periféria-egységből áll. Mindegyik program egy igénynek felel meg, a központi egység a kiszolgáló egységeknek. Tegyük fel, hogy egy adott perifériát csak egy program használhat, és a periféria-egységben eltöltött időtartamok minden programra nézve független, azonos $\lambda$ paraméterű exponenciális eloszlású valószínűségi változók. Miután a program bizonyos időt eltöltött a periférián, átkerül a központi egységbe, és itt azonnal megkezdődik a kiszolgálása, amelynek az időtartama $\beta<\infty$ várható értékű, $G(x)$ eloszlásfüggvényű valószínűségi változó $\left(G\left(0^+\right)=0\right)$. A központi egységben a programok kiszolgálása Processor Sharing (PS)-elv szerint történik, azaz hogyha a $(t,t+\delta t)$ időintervallumban egyidűleg $k$ programot szolgálnak ki, akkor az egyes jobok kiszolgálási ideje csak $\delta t/k$-val halad előre. A programok kiszolgálásuk után abba a perifériába kerülnek vissza, ahonnan érkeztek. Ebben a modellben a segédváltozók módszerét fogjuk alkalmazni a rendszert leíró sztochasztikus folyamat megadásánál. Vezessük be a következő valószínűségi változókat: $\nu(t)$: a $t$-edik időpillanatban a CPU-nál tartózkodó igények száma, $\xi_1(t),\ldots ,\xi_{\nu(t)}(t)$: a $t$-edik időpillanatban a CPU-nál tartózkodó igények eltelt kiszolgálási ideje $\nu(t)>0$ esetben. Látható, hogy az

\begin{displaymath}X(t)=\left(\nu(t); \xi_1(t),\ldots ,\xi_{\nu(t)}(t)\right) \end{displaymath}

sztochasztikus folyamat olyan Markov-folyamat, melynek állapotterét egy diszkrét komponensből és több folytonos komponensből álló vektorok alkotják. Az ilyen típusú folyamatokat szakaszonként lineáris Markov-folyamatoknak nevezzük. Meg kell jegyeznünk, hogy nagyon sok problémát ilyen folyamattal tudunk hűen leírni. Részletes tanulmányozásra ajánljuk Gnedenko-Kovalenko (1989)-könyvét. Legyen

\begin{displaymath}P_k\left(t,x_1,\ldots,x_k\right)dx_1\ldots dx_k=P\left(\nu(t)=k; x_i\le\xi_i< x_i+dx_i, i=1,\ldots,k\right) , \end{displaymath}

azaz $P_k(t,x_1,\ldots,x_k)$, $k=1,\ldots,n$ annak a valószínűsége, hogy a központi egységnél a $t$ időpontban $k$ job tartózkodik, és az egyes jobok kiszolgálásából $x_1,\ldots,x_k$ hosszúságú idő telt el. Legyen $\delta$ megfelelően kicsi pozitív szám. Ekkor $P_k(t,x_1,\ldots,x_k)$- ra $(k=1,\ldots,n-1)$ a következő összefüggés írható fel:

\begin{displaymath}P_k\left(t;x_1,\ldots, x_k\right)=\end{displaymath}




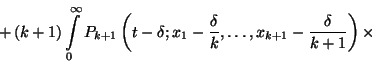
\begin{displaymath}+\left(k+1\right)\int\limits_0^\infty P_{k+1}\left(t-\delta;... ...\delta\over k}, \ldots, x_{k+1}-{\delta\over k+1}\right)\times\end{displaymath}


\begin{displaymath}\times\prod_{i=1}^k {1-G\left(x_i\right)\over 1-G\left(x_i-{\... ...ht]\over 1-G\left[x_{k+1}- {\delta\over k+1}\right]} dx_{k+1}.\end{displaymath}

A jobb oldal első tagja azt írja le, hogy a $(t-\delta,t)$ időintervallumban nem fejeződik be egyetlen kiszolgálás sem. A második tag pedig azt, hogy ebben az időintervallumban a $(k+1)$ egy program közül egy kiszolgálása fejeződik be. Mindkét oldalt $\prod\limits _{i=1}^k \left[1-G\left(x_i\right)\right]$-vel osztva, és $\delta\to 0$, $t\to\infty$ határértéket véve kapjuk, hogy

\begin{displaymath}\left[{1\over k}\sum_{i=1}^k{\partial\over \partial x_i}+\lambda\left(n-k\right)\right] q_{ _k}\left(x_1, \ldots,x_k\right)=\end{displaymath}


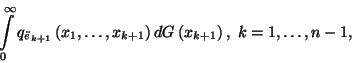
\begin{displaymath}\int\limits_0^\infty q_{ ë_{k+1}}\left(x_1,\ldots,x_{k+1}\right)dG\left(x_{k+1}\right),\ k=1,\ldots,n-1,\end{displaymath}

ahol $q_k\left(x_1,\ldots,x_k\right)=\lim\limits_{t \to \infty} P_k\left(t;x_1,\ldots,x_k\right) /\prod\limits_{i=1}^k \left[1-G\left(x_i\right)\right]$. $P_0$-ra és $q_n(x_1,\ldots,x_n)$-re hasonlóan kapjuk:

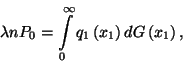
\begin{displaymath}\lambda nP_0= \int\limits_0^\infty q_1\left(x_1\right)dG\left(x_1\right),\end{displaymath}


\begin{displaymath}{1\over n} \sum_{i=1}^n {\partial\over \partial x_i} q_nŽ\left(x_1,\ldots,x_n\right)=0.\end{displaymath}

Ezek az egyenletek nem írják le teljesen a rendszer működését, mivel nem veszik figyelembe az esetleges ugrásszerű átmeneteket azokban a pillanatokban, amikor a programok a perifériákból a központi egységbe kerülnek. A hiányzó egyenleteket hasonlóan kapjuk meg:

\begin{displaymath}q_1\left(0\right)=\lambda n P_0,\end{displaymath}


\begin{displaymath}q_k\left(0,x_1,\ldots,x_{k-1}\right) = \lambda \left(n-k+1\right)q_{k-1}\left(x_1,\ldots,x_{k-1}\right), \end{displaymath}


\begin{displaymath}k=1,\ldots,n. \end{displaymath}

A kapott integro-differenciál egyenletek megoldását közvetlen helyettesítéssel nyerjük:

\begin{displaymath}q_k\left(x_1,\ldots,x_k\right)=P_0\lambda ^kn!/\left[\left(n-k\right)!\right],\end{displaymath}

és

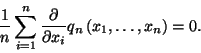
\begin{displaymath}P_k\left(x_1,\ldots,x_k\right)=P_0\lambda ^k{n!\over \left(n-k\right)!} \prod_{i=1}^k \left[1-G\left(x_i\right)\right],\end{displaymath}


\begin{displaymath}i=1,\ldots,n.\end{displaymath}

Legyen $P_k$ annak a stacionárius valószínűsége, hogy tetszőleges időpontban a központi egységben $k$ program tartózkodik. Nyilvánvalóan

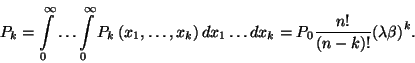
\begin{displaymath}P_k=\int\limits_0^\infty \ldots \int\limits_0^\infty P_k\lef... ...= P_0{n!\over \left(n-k\right)!}{\left(\lambda\beta\right)}^k.\end{displaymath}

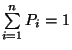A $P_0$ valószínűséget a $\sum\limits_{i=1}^n P_i=1$ normalizáló feltételből kapjuk meg.

Nyitólap    Tartalomjegyzék    Fejezetek ( B I II III IV F )    Letöltések
FRAME-mel FRAME nélkül
<<   Előző Következő  >>