III.2.3. A rendszer jellemzőinek meghatározása
6. Tétel. Az össztermelés várható
időtartama a  intervallumban stacionárius folyamat esetén
intervallumban stacionárius folyamat esetén
Bizonyítás. Esetünkben
és 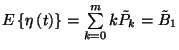 , ahol
, ahol  -ot
-ot  adja. Behelyettesítés után megkapjuk
az állítást. 1. Következmény. Jelölje
adja. Behelyettesítés után megkapjuk
az állítást. 1. Következmény. Jelölje 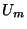 az átlagos összgépkihasználtságot, vagyis
legyen
az átlagos összgépkihasználtságot, vagyis
legyen
A 6. Tétel következményeként adódik, hogy egy gép
kihasználtsága
7. Tétel. Jelölj 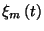 a következő valószínűségi változót
a következő valószínűségi változót
Ekkor stacinárius folyamat esetén a szerelő 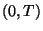 időközben javítással töltött
idejének várható értéke
időközben javítással töltött
idejének várható értéke
Bizonyítás. Fennáll, hogy
A 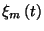 valószínűségi változó
várható értéke a következőképpen határozható
meg:
valószínűségi változó
várható értéke a következőképpen határozható
meg:
ahol 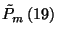 alapján kiszámolható. Ezt
beírva kapjuk az állítást. 2. Következmény. Jelölje
alapján kiszámolható. Ezt
beírva kapjuk az állítást. 2. Következmény. Jelölje
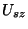 a ,,szerelő " kihasználtságát, amit a következőképpen
definiálunk:
a ,,szerelő " kihasználtságát, amit a következőképpen
definiálunk:
A 7. Tétel következményeként adódik, hogy
Jelölje 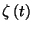 a
a 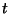 időpontban meghibásodott gépnek a javítás megkezdéséig
tartó várakozási idejét. Ez megfelel annak az időnek, ameddig
a szerelő elvégzi a
időpontban meghibásodott gépnek a javítás megkezdéséig
tartó várakozási idejét. Ez megfelel annak az időnek, ameddig
a szerelő elvégzi a 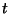 pillanatban álló gépek javítását, feltéve,
hogy közben nem áll be a várakozók sorába. Legyen
pillanatban álló gépek javítását, feltéve,
hogy közben nem áll be a várakozók sorába. Legyen ![$[x]^+=\cases{x,& ha $x>0$,\cr
0,& ha $x\le 0$\cr}$](img58.gif) . Ekkor fennáll, hogy
. Ekkor fennáll, hogy
ahol 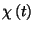 az eddigi jelölésnek megfelelően a
az eddigi jelölésnek megfelelően a 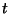 pillanatban (esetleg) folyamatban lévő javítás befejezéséhez
szükséges időt jelenti,
pillanatban (esetleg) folyamatban lévő javítás befejezéséhez
szükséges időt jelenti, 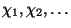
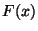 eloszlásfüggvényű független valószínűségi
változók, melyek
eloszlásfüggvényű független valószínűségi
változók, melyek 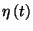 -től és
-től és 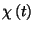 -től is függetlenek.
-től is függetlenek. 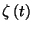 -t szokás virtuális várakozási
időnek is nevezni. A várakozási idő eloszlásfüggvénye
stacionáris esetben
-t szokás virtuális várakozási
időnek is nevezni. A várakozási idő eloszlásfüggvénye
stacionáris esetben 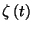 előbbi alakjának felhasználásával
előbbi alakjának felhasználásával
ahol 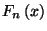 jelöli az
jelöli az 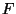 eloszlásfüggvénynek önmagával vett
eloszlásfüggvénynek önmagával vett 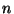 -szeres konvolucióját (
-szeres konvolucióját ( 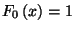 , ha
, ha 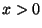 és
és 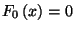 , ha
, ha 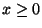 ). 8. Tétel. Ha
). 8. Tétel. Ha 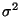 véges, akkor a várakozási idő várható
értéke
véges, akkor a várakozási idő várható
értéke
Bizonyítás. Mivel a folyamat stacionárius, ezért
bármely 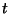 -re. Az 5. Tétel felhasználásával kapjuk, hogy
-re. Az 5. Tétel felhasználásával kapjuk, hogy
Ekkor
Mivel 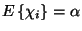 ,
, 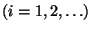 és
és 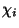 -k függetlenek,
-k függetlenek,
adódik. A 3. Tétel alapján érvényesek a következő
egyenlőségek
és
Behelyettesítés után kapjuk, hogy
ezzel a tételt bebizonyítottuk. 9. Tétel. Jelentse 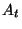 azt az eseményt, hogy a
azt az eseményt, hogy a 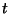 pillanatban történik leállás. A várakozási
idő eloszlásfüggvénye
pillanatban történik leállás. A várakozási
idő eloszlásfüggvénye 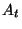 feltétel mellett
feltétel mellett
a várakozási idő várható értéke 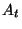 feltétel mellett (amit az aktuális várakozási
idő várható értékének is szoktak nevezni)
feltétel mellett (amit az aktuális várakozási
idő várható értékének is szoktak nevezni)
Bizonyítás. A várakozási idő eloszlásfüggvénye
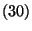 szerint
szerint
Könnyű látni, hogy
A feltételes valószínűség definíciója szerint
Mivel 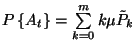 , így
, így  -ból következik
-ból következik 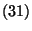 . A feltételes várható értéket
a következőképpen határozhatjuk meg.
. A feltételes várható értéket
a következőképpen határozhatjuk meg. 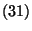 miatt nyilvánvalóan fennáll
miatt nyilvánvalóan fennáll
Mivel teljesül a
egyenlőség, a jobb oldal kiszámításhoz szükségünk
van 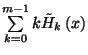 meghatározására.
Erre érvényes
meghatározására.
Erre érvényes
ahol
A 3. tétel szerint
ezért összegükre teljesül
Ekkor
Mindezek figyelembevételével adódik, hogy
Folytassuk a feltételes várható érték képletében
szereplő mennyiségek kiszámítását. Látható,
hogy
valamint
A megfelelő tagokat  -be visszahelyettesítve rövid számolás után
kapjuk az állítást. Ugyanis a nevező
-be visszahelyettesítve rövid számolás után
kapjuk az állítást. Ugyanis a nevező
amivel a számláló minden tagja osztható. Ekkor
a tételt ezzel bebizonyítottuk. Vezessük le ezt az összefüggést
más eszközökkel is. Az előzőekhez hasonlóan belátható,
hogy
ahol 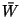 egy gép aktuális átlagos várakozási
ideje. Mivel
egy gép aktuális átlagos várakozási
ideje. Mivel
és
ezért
Ebből
A modell tovább általánosítható oly módon, hogy
a gépek meghibásodási intenzitása és a kiszolgálási
idő függ a gép indexétől. Ez az 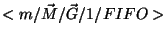 rendszer, amellyel Sztrik (1981, 1983), Sztrik-Tomkó
(1982) foglalkozik.
rendszer, amellyel Sztrik (1981, 1983), Sztrik-Tomkó
(1982) foglalkozik.
![]() intervallumban stacionárius folyamat esetén
intervallumban stacionárius folyamat esetén
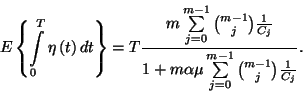
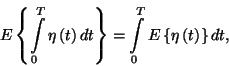
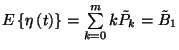 , ahol
, ahol 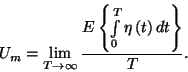
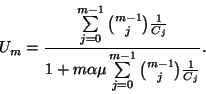
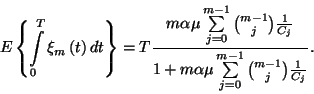
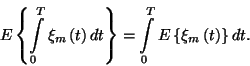
![$[x]^+=\cases{x,& ha $x>0$,\cr
0,& ha $x\le 0$\cr}$](img58.gif) . Ekkor fennáll, hogy
. Ekkor fennáll, hogy ![\begin{displaymath}\zeta\left(t\right)=\chi\left(t\right)+\sum_{i=1}^{{\left[m-1-\eta\left
(t\right)\right]}^{+}}\chi_i,\leqno(29)\end{displaymath}](img59.gif)
![\begin{displaymath}E\left\{\chi\left(t\right)\ \vert\ \eta\left(t\right)<m\right...
...[1-F\left(x\right)\right]dx=
{\sigma^2+\alpha^2\over 2\alpha}.\end{displaymath}](img74.gif)
![\begin{displaymath}E\left\{\zeta\left(t\right)\right\}=\sum_{k=0}^{m-1}\tilde{P}...
...igma^2+\alpha^2\over 2\alpha}
+\left(m-1-k\right)\alpha\right]\end{displaymath}](img79.gif)
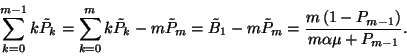
![\begin{displaymath}E\left\{\zeta\left(t\right)\right\}=\sum_{k=0}^{m-1}{m\alpha\...
...sigma^2+\alpha^2
\over 2\alpha}+\left(m-1\right)\alpha\right]+\end{displaymath}](img82.gif)
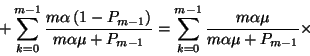
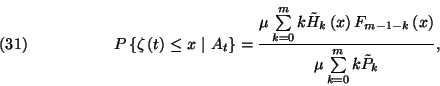

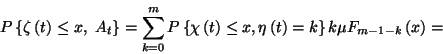
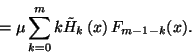
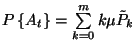 , így
, így ![\begin{displaymath}E\left\{\zeta\left(t\right)\ \vert\
A_t\right\}={\sum\limits...
...t)\alpha\right]\over\sum\limits_{k=0}^mk\tilde{P}_k}.\leqno(34)\end{displaymath}](img96.gif)
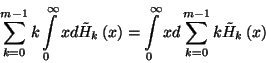
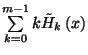 meghatározására.
Erre érvényes
meghatározására.
Erre érvényes 
![\begin{displaymath}\tilde{L}\left(x\right)={\int\limits_0^\infty e^{-\mu
x}\lef...
...nt\limits_0^\infty e^{-\mu x}\left[1-F\left(u\right)\right]du}.\end{displaymath}](img100.gif)
![\begin{displaymath}\sum_{k=0}^{m-1}k\tilde{P}_k=\sum_{k=0}^mk\tilde{P}_k-m\tilde{P}_m=
{1-\tilde{P}_m\over \alpha\mu}
\left[1-P_{m-1}\right].\end{displaymath}](img103.gif)
![\begin{displaymath}\sum_{k=0}^{m-1}k\left(m-1\right)\alpha
\tilde{P}_k=\left(m-...
...ht)\alpha{1-\tilde{P}_m\over \alpha\mu}\left[1-P_{m-1}\right], \end{displaymath}](img106.gif)
![\begin{displaymath}\sum_{k=0}^{m-1}k^2\alpha \tilde{P}_k=\alpha\sum_{k=0}^{m-1}k
\left[{1-\tilde{P}_m\over
\alpha\mu} P_{k-1}\right]=\end{displaymath}](img107.gif)
![\begin{displaymath}={1-\tilde{P}_m\over
\mu}\sum_{k=0}^{m-1}\left[\left(k-1\right)P_{k-1}+P_{k-1}\right]=\end{displaymath}](img108.gif)
![\begin{displaymath}={1-\tilde{P}_m\over
\mu}\left[\sum_{k=0}^{m-2}kP_k+\sum_{k=0}^{m-2}P_k\right]=\end{displaymath}](img109.gif)
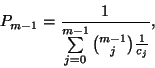
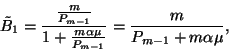
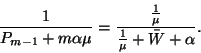
![]() rendszer, amellyel Sztrik (1981, 1983), Sztrik-Tomkó
(1982) foglalkozik.
rendszer, amellyel Sztrik (1981, 1983), Sztrik-Tomkó
(1982) foglalkozik.