III.2.2. Stacionárius folyamat
4. Tétel. Ha 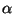 véges, akkor tetszőleges
véges, akkor tetszőleges 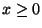 esetén létezik a
esetén létezik a
határeloszlás, és fennáll
ha 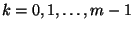 és
és 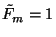 . Bizonyítás. Vizsgáljuk először
a
. Bizonyítás. Vizsgáljuk először
a
együttes eloszlásfüggvényt. A 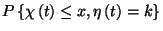 valószínűséget a következő
alakba írhatjuk fel:
valószínűséget a következő
alakba írhatjuk fel:
Az egyenlőség igazolása 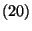 bizonyításához hasonlóan történik.
Határértéket képezve adódik, hogy
bizonyításához hasonlóan történik.
Határértéket képezve adódik, hogy
miközben felhasználtuk az 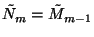 és az
és az
egyenlőségeket. 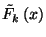 -re a következő összefüggés
írható fel
-re a következő összefüggés
írható fel
Ismerve a 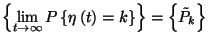 és a
és a 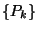 eloszlások közötti
eloszlások közötti 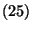 összefüggést, következik a tétel
állítása. Definíció. Az általunk vizsgált folyamatot
stacionáriusnak nevezzük, ha a folyamat kezdeti eloszlását
a
összefüggést, következik a tétel
állítása. Definíció. Az általunk vizsgált folyamatot
stacionáriusnak nevezzük, ha a folyamat kezdeti eloszlását
a 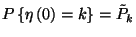 és
és 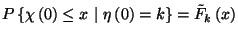 ,
, 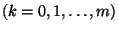 valószínűségek adják.
Ekkor az
valószínűségek adják.
Ekkor az 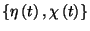 változópár
eloszlása minden időpontban megegyezik a kezdeti eloszlással és
változópár
eloszlása minden időpontban megegyezik a kezdeti eloszlással és
valamint
ahol 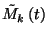 és
és 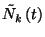 az eddigi jelölésnek megfelelően
a
az eddigi jelölésnek megfelelően
a 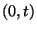 -ben előforduló
-ben előforduló 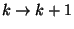 ill.
ill. 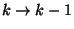 átmenetek várható száma. Most néhány
állítást bizonyítunk be a stacionárius folyamatra.
átmenetek várható száma. Most néhány
állítást bizonyítunk be a stacionárius folyamatra.
![]() véges, akkor tetszőleges
véges, akkor tetszőleges ![]() esetén létezik a
esetén létezik a 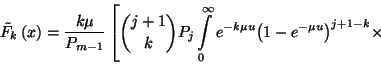
![\begin{displaymath}\times\left.\int\limits_0^\infty e^{-k\mu u}{\left(1-e^{-\mu
...
...m-1-k}\left[F\left(u+x\right)-F\left(u\right)\right]du\right] ,\end{displaymath}](img6.gif)
![\begin{displaymath}P\left\{\chi\left(t\right)\le
x,\eta\left(t\right)=k\right\}...
...ght)-q_j
\left(t+x\right)\right]{j\choose k} e^{-k\mu x}\times\end{displaymath}](img11.gif)
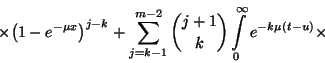
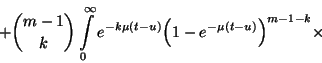
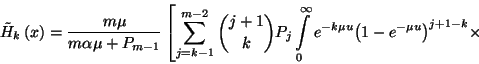
![\begin{displaymath}\left.\times\int\limits_0^\infty e^{-k\mu u}{\left(1-e^{-\mu
...
...m-1-k}\left[F\left(u+x\right) -F\left(u\right)\right]du\right],\end{displaymath}](img19.gif)
![]() és
és ![]() az eddigi jelölésnek megfelelően
a
az eddigi jelölésnek megfelelően
a ![]() -ben előforduló
-ben előforduló ![]() ill.
ill. ![]() átmenetek várható száma. Most néhány
állítást bizonyítunk be a stacionárius folyamatra.
átmenetek várható száma. Most néhány
állítást bizonyítunk be a stacionárius folyamatra.