III.2.1.2. A 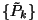 valószínűségeloszlás meghatározása
valószínűségeloszlás meghatározása
2. Tétel. Ha 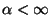 , akkor az
, akkor az 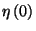 valószínűségi változó kezdeti
eloszlásától függetlenül létezik a
valószínűségi változó kezdeti
eloszlásától függetlenül létezik a 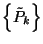 határeloszlás és fennáll:
határeloszlás és fennáll:
ahol 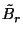 a
a 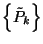 valószínűségeloszlás
valószínűségeloszlás
 -edik binomiális momentuma, melyre teljesül
-edik binomiális momentuma, melyre teljesül 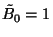 és
és 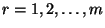 -re
-re
ahol 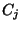 jelentése változatlan. Néhány segédtételre
lesz szükségünk a bizonyításhoz. 1. Segédtétel.
Jelölje
jelentése változatlan. Néhány segédtételre
lesz szükségünk a bizonyításhoz. 1. Segédtétel.
Jelölje 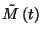 a
a 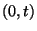 időközben előforduló
időközben előforduló 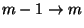 átmenetek várható számát. Tetszőleges
átmenetek várható számát. Tetszőleges
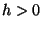 -re fennáll:
-re fennáll:
A segédtétel a következőképpen igazolható. Tekintsük
az 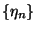 Markov-láncnál az
Markov-láncnál az 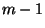 állapotot. Az
állapotot. Az 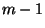 visszatérő állapot és a visszatérésig
megtett lépések számának várható értéke
visszatérő állapot és a visszatérésig
megtett lépések számának várható értéke
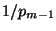 . Két egymást követő
. Két egymást követő 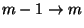 átmenet között eltelt időtartam a ,,szerelő"
szempontjából egy szünetből és egy javítási periódusból
tevődik össze. A szünet hosszának várható értéke
átmenet között eltelt időtartam a ,,szerelő"
szempontjából egy szünetből és egy javítási periódusból
tevődik össze. A szünet hosszának várható értéke
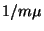 , a javítási periódus hosszának várható
értéke
, a javítási periódus hosszának várható
értéke 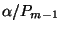 , ahol
, ahol 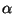 egy javítás átlagos időtartama, az egy javítási
periódusban végzett javítások várható száma
egy javítás átlagos időtartama, az egy javítási
periódusban végzett javítások várható száma
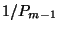 . Az egymást követő
. Az egymást követő 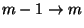 átmenetek között eltelt időtartamok egyforma
eloszlású független valószínűségi változók,
közös várható értékük a fentiek szerint a
átmenetek között eltelt időtartamok egyforma
eloszlású független valószínűségi változók,
közös várható értékük a fentiek szerint a 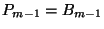 egyenlőség figyelembe vételével
egyenlőség figyelembe vételével
 bal oldala viszont egyenlő ennek a várható
értéknek a reciprok értékével. D. Blackwell tétele
- az I. fejezetbben említett
bal oldala viszont egyenlő ennek a várható
értéknek a reciprok értékével. D. Blackwell tétele
- az I. fejezetbben említett  Tétel - alapján létezik a következő határérték,
és fennáll, hogy
Tétel - alapján létezik a következő határérték,
és fennáll, hogy
ami megegyezik  -gyel. 2. Segédtétel. Jelölje
-gyel. 2. Segédtétel. Jelölje 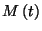 a
a 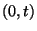 időközben előforduló
időközben előforduló 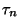 időpontok várható számát, azaz a
időpontok várható számát, azaz a 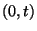 időközben befejeződő javítások várható
számát. Tetszőleges
időközben befejeződő javítások várható
számát. Tetszőleges 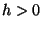 -ra fennáll, hogy
-ra fennáll, hogy
A segédtétel bizonyítását egy jelölés bevezetésével
kezdjük. Jelölje 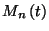 a
a 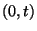 időközben befejeződő olyan javítások
várható számát, amelyek egy javítási periódus
időközben befejeződő olyan javítások
várható számát, amelyek egy javítási periódus
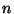 -edik javítását követik. Ekkor
-edik javítását követik. Ekkor 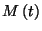 a következő alakba írható:
a következő alakba írható:
Az egymást követő javítási periódusok 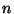 -edik javításának befejeződési időpontjai közötti
időtartamok egyforma eloszlású, független valószínűségi
változók. Blackwell már említett tétele miatt létezik
a
-edik javításának befejeződési időpontjai közötti
időtartamok egyforma eloszlású, független valószínűségi
változók. Blackwell már említett tétele miatt létezik
a
határérték, ami megegyezik a
határértékkel, ez viszont könnyen kiszámolható.
Jelölje ugyanis 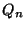 annak a valószínűségét, hogy egy javítási
periódus legalább
annak a valószínűségét, hogy egy javítási
periódus legalább 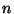 javításból áll. Ekkor felírható, hogy
javításból áll. Ekkor felírható, hogy
Felhasználva az 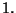 Segédtételt, azt kapjuk, hogy
Segédtételt, azt kapjuk, hogy
Egy javítási periódusban végzett javítások várható
száma
tehát 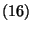 szerint
szerint
Ebben a kifejezésben a határérték tagonként vehető, mert
a sor egyenletesen konvergens, ugyanis az
egyenlőség felhasználásával
adódik. A 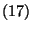 egyenlőségbe
egyenlőségbe 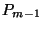 értékét beírva megkapjuk a segédtétel
állítását. 3. Segédtétel. Jelölje
értékét beírva megkapjuk a segédtétel
állítását. 3. Segédtétel. Jelölje 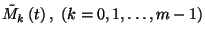 a
a 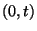 intervallumban előforduló
intervallumban előforduló 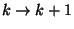 átmenetek várható számát. Tetszőleges
átmenetek várható számát. Tetszőleges
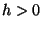 esetén fennáll, hogy
esetén fennáll, hogy
Ezt az állítást 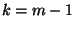 -re már bebizonyítottuk az 1. Segédtételben.
A
-re már bebizonyítottuk az 1. Segédtételben.
A 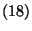 baloldalán álló határérték
létezését D. Blackwell tétele bizonyítja, ugyanis az
egymást követő
baloldalán álló határérték
létezését D. Blackwell tétele bizonyítja, ugyanis az
egymást követő 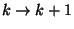 átmenetek közötti időtartamok egyforma eloszlású,
független változók, eloszlásuk eleget tesz az említett
tételek feltételeinek. A
átmenetek közötti időtartamok egyforma eloszlású,
független változók, eloszlásuk eleget tesz az említett
tételek feltételeinek. A 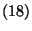 határérték megegyezik a
határérték megegyezik a 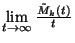 határértékkel,
ami nyilván
határértékkel,
ami nyilván 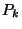 -szorosa a
-szorosa a 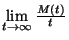 határértéknek,
vagyis
határértéknek,
vagyis 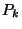 -szorosa
-szorosa 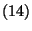 -nek. Rátérünk a tétel bizonyítására,
vagyis a
-nek. Rátérünk a tétel bizonyítására,
vagyis a 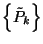 eloszlás meghatározására.
Ha
eloszlás meghatározására.
Ha 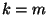 , akkor
, akkor
és 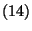 miatt
miatt 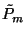 létezése bizonyítható. Ekkor
létezése bizonyítható. Ekkor
Jelölje 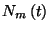 a
a 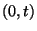 időközben előforduló
időközben előforduló 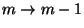 átmenetek várható számát. Ekkor
igaz az
átmenetek várható számát. Ekkor
igaz az
egyenlőség, amiből
következik. 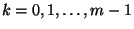 esetén a
esetén a 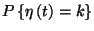 valószínűség a következő
formában írható fel:
valószínűség a következő
formában írható fel:
ahol 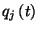 annak a valószínűsége, hogy a rendszer
kezdő állapota
annak a valószínűsége, hogy a rendszer
kezdő állapota 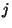 volt és a
volt és a ![$(0,t]$](img163.gif) intervallumban nem fejeződött be kiszolgálás. A
intervallumban nem fejeződött be kiszolgálás. A
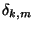 jelentése pedig:
jelentése pedig: 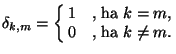 A
A 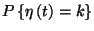 valószínűség előző
felírása következőképpen indokolható: az
valószínűség előző
felírása következőképpen indokolható: az  esemény több egymást kizáró
eseményból tevődik össze a) a kezdő állapot
esemény több egymást kizáró
eseményból tevődik össze a) a kezdő állapot 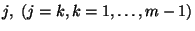 és a
és a 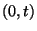 intervallumban nem fejeződik be javítás,
s ez idő alatt leáll
intervallumban nem fejeződik be javítás,
s ez idő alatt leáll 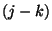 gép, b) az
gép, b) az 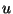 időpillanatban
időpillanatban 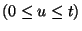 történik egy
történik egy 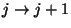 átmenet
átmenet 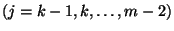 , az
, az ![$\left(u,t\right]$](img172.gif) intervallumban nem fejeződik be kiszolgálás
és leáll
intervallumban nem fejeződik be kiszolgálás
és leáll 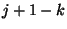 gép, c) az
gép, c) az 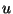 időpontban
időpontban 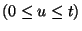 történik egy
történik egy 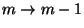 átmenet, az
átmenet, az ![$\left(u,t\right]$](img172.gif) intervallumban nem fejeződik be javítás és
leáll
intervallumban nem fejeződik be javítás és
leáll 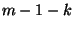 gép. Vezessük be a következő jelöléseket:
gép. Vezessük be a következő jelöléseket:
Ezek a határértékek Blackwell tétele miatt tetszőleges 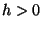 esetén léteznek. Ekkor
esetén léteznek. Ekkor 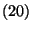 alapján
alapján
ahol
és
Határozzuk meg a 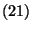 egyenlet
egyenlet 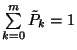 feltételnek eleget tevő megoldásait!
Ha
feltételnek eleget tevő megoldásait!
Ha 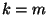 , akkor
, akkor 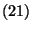 -ből azonnal következik, hogy
-ből azonnal következik, hogy
Vezessük be az
generátorfüggvényt. Ekkor
ahol  a
a 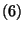 -os generátorfüggvény. Vezessük be
a
-os generátorfüggvény. Vezessük be
a 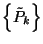 valószínűségeloszlás
valószínűségeloszlás
binomiális momentumait. Látható, hogy 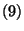 -hez hasonlóan
-hez hasonlóan
és 
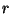 -szeres differenciálásával a
-szeres differenciálásával a
összefüggéshez jutunk.
figyelembevételével és
 felhasználásával a következő egyenletet írhatjuk fel:
felhasználásával a következő egyenletet írhatjuk fel:
és
Írjuk be a 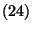 -es egyenletbe
-es egyenletbe 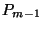 és
és 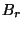 értékét! Ekkor
értékét! Ekkor
ami megegyezik 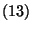 -mal. A
-mal. A 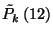 -beli alakját
-beli alakját 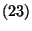 -ból megkapjuk, ha a
-ból megkapjuk, ha a 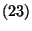 egyenletek mindkét oldalát
egyenletek mindkét oldalát 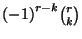 -val megszorozzuk és az így kapott egyenleteket összeadjuk.
Ezzel a tételt bizonyítását befejeztük. 3. Tétel.
A
-val megszorozzuk és az így kapott egyenleteket összeadjuk.
Ezzel a tételt bizonyítását befejeztük. 3. Tétel.
A 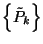 és a
és a 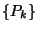 valószínűségeloszlás a következő
kapcsolatban áll egymással:
valószínűségeloszlás a következő
kapcsolatban áll egymással:
és
Bizonyítás. Nyilvánvaló, hogy az adott idő alatt előforduló
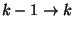 és
és 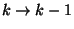 átmenetek száma legfeljebb
átmenetek száma legfeljebb 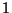 -gyel különbözhet egymástól. Ez természetesen
a várható értékükre is fennáll. Ha
-gyel különbözhet egymástól. Ez természetesen
a várható értékükre is fennáll. Ha 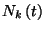 jelöli a
jelöli a 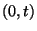 időközben előforduló
időközben előforduló 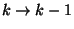 átmenetek várható számát, akkor
átmenetek várható számát, akkor
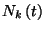 -re fennáll
-re fennáll
Így
A 3. Segédtétel szerint
Mivel 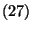 és
és  a fenti egyenlőtlenség miatt megegyezik, ezért
a fenti egyenlőtlenség miatt megegyezik, ezért
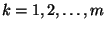 -re megkaptuk
-re megkaptuk 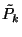
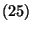 -beli alakját. A
-beli alakját. A 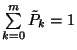 egyenlőség fennállása
miatt
egyenlőség fennállása
miatt 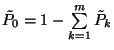 , ami megegyezik
, ami megegyezik  -tal.
-tal.
 valószínűségeloszlás meghatározása
valószínűségeloszlás meghatározása
![]() , akkor az
, akkor az ![]() valószínűségi változó kezdeti
eloszlásától függetlenül létezik a
valószínűségi változó kezdeti
eloszlásától függetlenül létezik a ![]() határeloszlás és fennáll:
határeloszlás és fennáll:
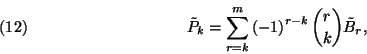
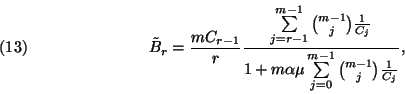
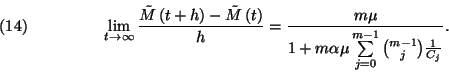
![\begin{displaymath}{1\over m\mu}+{\alpha\over P_{m-1}}={1\over m\mu}\left[1+m\alpha\mu
\sum_{j=0}^{m-1}
{m-1\choose j}{1\over C_j}\right].\end{displaymath}](img115.gif)
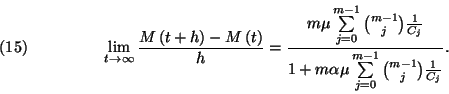

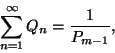
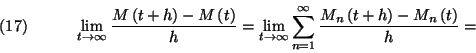
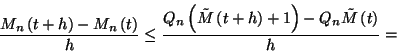
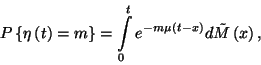
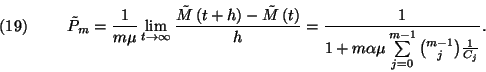
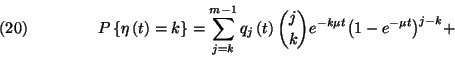
![\begin{displaymath}+\delta_{k,m}\left[P\left\{\eta\left(0\right)=m\right\}e^{-m\...
...left(t-u\right)}\right)d\tilde{M}_{m-1}
\left(u\right)\right]+\end{displaymath}](img157.gif)
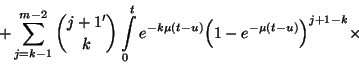
![\begin{displaymath}\times\left[1-F\left(t-u\right)\right]d\tilde{M}_j\left(u\right)+{m-1\choose
k}\int\limits_0^t e^{-k\mu\left(t-u\right)}\times\end{displaymath}](img159.gif)
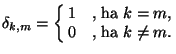 A
A 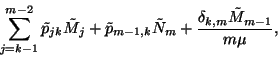
![\begin{displaymath}\tilde{p}_{jk}={j+1\choose k}\int\limits_0^\infty e^{-k\mu x}...
...1-e^{-\mu x}
\right)}^{j+1-k}\left[1-F\left(x\right)\right]dx,\end{displaymath}](img181.gif)
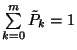 feltételnek eleget tevő megoldásait!
Ha
feltételnek eleget tevő megoldásait!
Ha 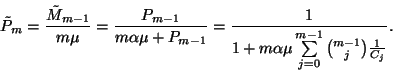
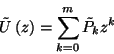
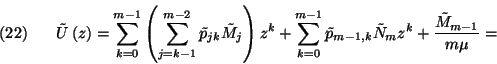
![\begin{displaymath}=\sum_{k=0}^{m-1}\Biggl(\sum_{j=k-1}^{m-2}{j+1\choose k}\int\...
...-\mu x}\right)}^{j+1-k}\left[1-F\left(x\right)\right]
dx\times\end{displaymath}](img189.gif)
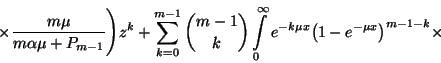
![\begin{displaymath}={m\mu\over m\alpha\mu+P_{m-1}}\left[\sum_{k=0}^{m-2}\int\lim...
...{-\mu
x}\right)}^{k+1}\left[1-F\left(x\right)\right]dx+\right.\end{displaymath}](img192.gif)
![\begin{displaymath}\left.+\int\limits_0^\infty P_{m-1}{\left(1-e^{-\mu x}+ze^{-\...
...eft[1-F\left(x\right)\right]dx +{P_{m-1}\over
m\mu}z^m\right]=\end{displaymath}](img193.gif)
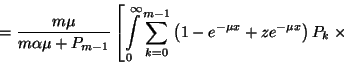
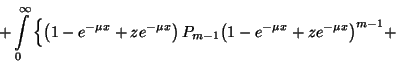
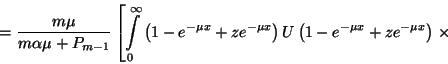
![\begin{displaymath}\left.\times\int\limits_0^\infty e^{-\mu
x}{\left(1-e^{-\mu ...
...left[1-F\left(x\right)\right]dx+{P_{m-1}\over m\mu}z^m\right] ,\end{displaymath}](img201.gif)
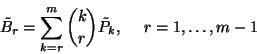
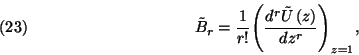
![\begin{displaymath}\times\left[\int\limits_0^\infty e^{-r\mu
x}\left[1-F\left(x\right)\right]dx+{1\over m\mu}{m\choose r}P_{m-1}\right]\end{displaymath}](img208.gif)
![\begin{displaymath}\int\limits_0^\infty e^{-r\mu
x}\left[1-F\left(x\right)\right]dx={1-\varepsilon_r\over\mu r}\end{displaymath}](img209.gif)
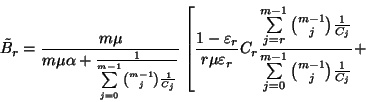
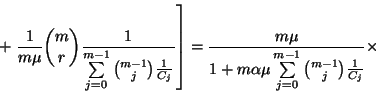
![\begin{displaymath}\times\left[{C_{r-1}\over r\mu}\sum_{j=r}^{m-1}{m-1\choose j}...
... C_j}+
{C_{r-1}\over m\mu}{m\choose r}{1\over C_{r-1}}\right]=\end{displaymath}](img216.gif)
![\begin{displaymath}={m\mu\over 1+m\alpha\mu\sum\limits_{j=0}^{m-1}{m-1\choose j}...
...j}+
{C_{r-1}\over r} {m-1\choose r-1}{1\over C_{r-1}}\right] ,\end{displaymath}](img217.gif)
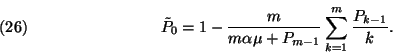
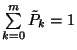 egyenlőség fennállása
miatt
egyenlőség fennállása
miatt 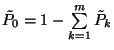 , ami megegyezik
, ami megegyezik