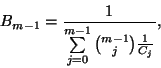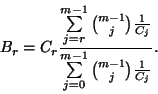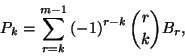III.2.1. A határeloszlások meghatározása
III.2.1.1 A 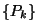 valószínűségeloszlás meghatározása
valószínűségeloszlás meghatározása
1. Tétel.
Az 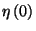 változó kezdeti eloszlásától
függetlenül létezik a
változó kezdeti eloszlásától
függetlenül létezik a 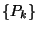 határeloszlás és fennáll
határeloszlás és fennáll
ahol
ahol 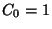 és
és 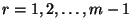 -re
-re
Bizonyítás. Látható, hogy az 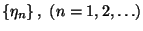 valószínűségi változók sorozata
Markov-láncot alkot
valószínűségi változók sorozata
Markov-láncot alkot
átmenetvalószínűségekkel, ahol 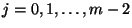 -re
-re
és
Ezt a következőkkel indokolhatjuk: az 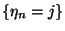 esemény azt jelenti, hogy
esemény azt jelenti, hogy 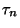 -ben befejeződik egy javítás, így
-ben befejeződik egy javítás, így 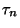 -ben a rendszer
-ben a rendszer 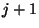 állapotban van, feltéve, hogy a
állapotban van, feltéve, hogy a 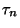 pillanatban nem romlott el gép. Ahhoz, hogy a rendszer
pillanatban nem romlott el gép. Ahhoz, hogy a rendszer 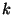 állapotba kerüljön az szükséges, hogy a
állapotba kerüljön az szükséges, hogy a ![$\left[\tau_n,\tau_{n+1}\right]$](img40.gif) időintervallumban pontosan
időintervallumban pontosan 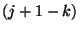 gép álljon le. A leálló gépek kiválasztása
gép álljon le. A leálló gépek kiválasztása
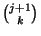 -féleképpen történhet. Az
-féleképpen történhet. Az 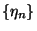 Markov-lánc ergodikus, mert az állapottér
elemeinek száma véges. Emiatt az
Markov-lánc ergodikus, mert az állapottér
elemeinek száma véges. Emiatt az 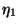 valószínűségi változó kezdeti eloszlásától
függetlenül léteznek a
valószínűségi változó kezdeti eloszlásától
függetlenül léteznek a
határvalószínűségşek, melyek a
egyenletrendszer
feltételnek eleget tevő megoldásai. A 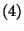 és
és 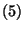 egyenletrendszer megoldására vezessük
be az
egyenletrendszer megoldására vezessük
be az
generátorfüggvényt. Ekkor 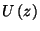 a következő alakra hozható:
a következő alakra hozható:
Vezessük be most a 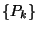 határeloszlás
határeloszlás
binomiális momentumait. Definíció szerint
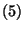 miatt
miatt 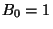 és
és 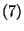 -ből
-ből 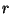 -szeres differenciálással kapjuk, hogy
-szeres differenciálással kapjuk, hogy
Legyen
Ekkor  a következő alakban írható:
a következő alakban írható:
ugyanis
A 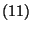 -es egyenletrendszer a
-es egyenletrendszer a 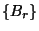 ismeretlenekre nézve egy változó együtthatós
lineáris differenciaegyenletrendszer. Az
ismeretlenekre nézve egy változó együtthatós
lineáris differenciaegyenletrendszer. Az
jelölések segítségével az egyenletrendszer
alakba írható át. Legyen 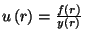 , ahol
, ahol 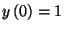 és
és 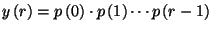 .
A
.
A 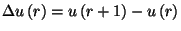 jelölés
mellett
jelölés
mellett
Ez alapján 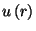 -re a következő összefüggés írható
fel:
-re a következő összefüggés írható
fel:
Ekkor
A 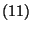 egyenletrendszer megoldása tehát
egyenletrendszer megoldása tehát
ahol 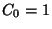 és
és
Ha 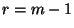 , akkor
, akkor
ennek felhasználásával
A 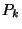 valószínűségek kifejezhetők a
valószínűségek kifejezhetők a 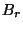 binomiális momentumokkal a
binomiális momentumokkal a 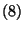 -as képlet segítségével. Szorozzuk
meg a
-as képlet segítségével. Szorozzuk
meg a 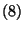 -as egyenletek mindkét oldalát
-as egyenletek mindkét oldalát 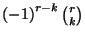 -val, és az így kapott egyenleteket
adjuk össze. Azt kapjuk, hogy
-val, és az így kapott egyenleteket
adjuk össze. Azt kapjuk, hogy
ezzel az állítást bebizonyítottuk.
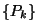 valószínűségeloszlás meghatározása
valószínűségeloszlás meghatározása
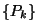 valószínűségeloszlás meghatározása
valószínűségeloszlás meghatározása
![]() változó kezdeti eloszlásától
függetlenül létezik a
változó kezdeti eloszlásától
függetlenül létezik a ![]() határeloszlás és fennáll
határeloszlás és fennáll 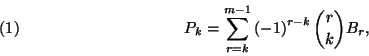
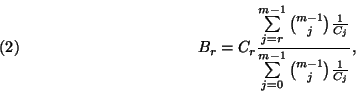

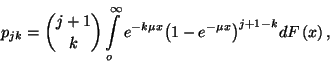
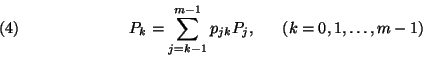


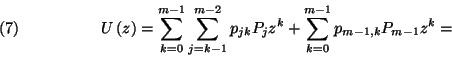
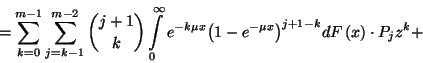
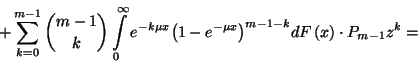
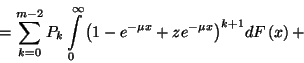
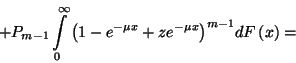
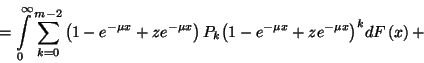
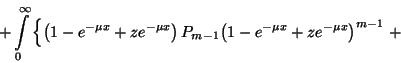
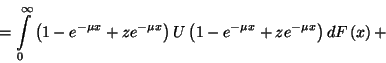
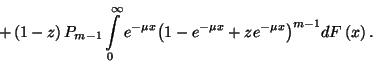

![\begin{displaymath}B_r=\left[B_r+B_{r-1}-{m-1\choose r-1}P_{m-1}\right]\int\limits_0^\infty
e^{-r\mu x}dF\left(x\right),\leqno(10)\end{displaymath}](img67.gif)
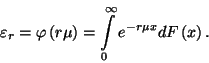
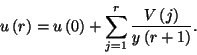
![\begin{displaymath}f\left(r\right)=y\left(r\right)\left[f\left(0\right)+
\sum_{j=0}^r{V\left(j\right)\over y\left(r+1\right)}\right].\end{displaymath}](img86.gif)
![\begin{displaymath}B_r=C_r\left[1-B_{m-1}\sum_{j=0}^{r-1}{m-1\choose j}{1\over C_j}\righet],\end{displaymath}](img87.gif)