III.4.1. A stacionárius eloszlás meghatározása
Jelölje a 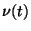 valószínűségi változó a
valószínűségi változó a 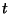 időpontban a terminálnál lévő jobok számát,
időpontban a terminálnál lévő jobok számát,
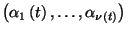 ezeknek a joboknak az indexeit lexikografikus sorrendben, és
ezeknek a joboknak az indexeit lexikografikus sorrendben, és 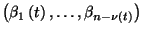 a központi egységnél lévő (kiszolgálás alatt lévő
vagy sorbanálló) jobok indexeit érkezésük sorrendjében.
Az
a központi egységnél lévő (kiszolgálás alatt lévő
vagy sorbanálló) jobok indexeit érkezésük sorrendjében.
Az
folyamat csak akkor Markov-folyamat, ha az 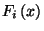
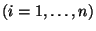 eloszlásfüggvények exponenciálisak.
Vezessük be a
eloszlásfüggvények exponenciálisak.
Vezessük be a 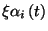 változót, amely azt az időt jelöli,
amelyet az
változót, amely azt az időt jelöli,
amelyet az 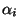 job a terminálnál eltöltött a legutolsó
központi egységbeli kiszolgálása óta. Az így kapott
job a terminálnál eltöltött a legutolsó
központi egységbeli kiszolgálása óta. Az így kapott
folyamat rendelkezik a Markov tulajdonsággal.
Jelölje 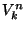 és
és 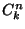 az
az 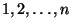 egészek
egészek 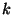 -ad osztályú variációinak illetve a kombinációinak
lexikografikusan rendezett halmazát. Ekkor az
-ad osztályú variációinak illetve a kombinációinak
lexikografikusan rendezett halmazát. Ekkor az 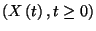 folyamat állapottere az olyan
folyamat állapottere az olyan
pontokból áll, ahol 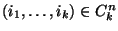 ,
, 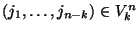 ,
, 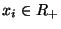 ,
, 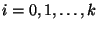 ,
, 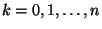 . Az
. Az 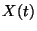 folyamat akkor van az
folyamat akkor van az 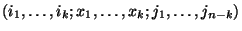 állapotban,
ha az
állapotban,
ha az 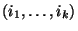 indexű jobok már
indexű jobok már 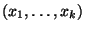 ideje vannak a termináloknál, és
ideje vannak a termináloknál, és 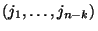 a központi egységnél lévő jobok
indexe érkezési sorrendben.
A Kolmogorov-egyenletek levezetéséhez szükségünk van
tetszőleges
a központi egységnél lévő jobok
indexe érkezési sorrendben.
A Kolmogorov-egyenletek levezetéséhez szükségünk van
tetszőleges 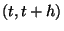 intervallumban lejátszódó átmenetek vizsgálatára.
Az átmeneti valószínűségeket a következő módon adhatjuk
meg
intervallumban lejátszódó átmenetek vizsgálatára.
Az átmeneti valószínűségeket a következő módon adhatjuk
meg 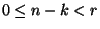 esetére.
esetére.
ahol 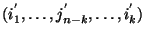 az
az 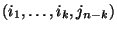 indexeket jelöli lexikografikus sorrendben, és
indexeket jelöli lexikografikus sorrendben, és 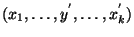 a megfelelő időket.
Ha
a megfelelő időket.
Ha 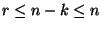 akkor az átmeneti valószínűségek a
következők:
akkor az átmeneti valószínűségek a
következők:
Vezessük be a következő függvényeket:
Legyen 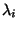 a következőképpen definiálva:
a következőképpen definiálva: 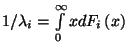 .
1.Tétel Ha
.
1.Tétel Ha 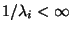 ,
, 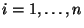 , akkor az
, akkor az 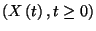 folyamatnak van egyértelmű
ergodikus ( stacionárius ) eloszlása, amely független a kezdeti
feltételektől, azaz
folyamatnak van egyértelmű
ergodikus ( stacionárius ) eloszlása, amely független a kezdeti
feltételektől, azaz
A tétel bizonyítása Gnedenko-Kovalenko (1989) könyvének
211. oldalán található tételből közvetlenül következik.
A tétel biztosítja a következő határértékek létezését,
és egyértelműségét:
ahol 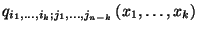 jelöli
az
jelöli
az 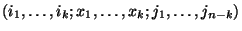 állapotok
sűrűségfüggvényét, ha
állapotok
sűrűségfüggvényét, ha 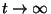 . Feltesszük, hogy rögzített
. Feltesszük, hogy rögzített 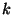 -ra az ergodikus eloszlásoknak létezik a sűrűségfüggvénye.
Ehhez elegendő feltenni, hogy az
-ra az ergodikus eloszlásoknak létezik a sűrűségfüggvénye.
Ehhez elegendő feltenni, hogy az 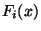 -nek van sűrűségfüggvénye. Vezessük be a
-nek van sűrűségfüggvénye. Vezessük be a
ún. norëmált sűrűségfüggvényeket.
2.Tétel A fenti normált sűrűségfüggvények kielégítik
az 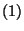 ,
, 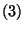 integro-differenciál-egyenleteket a
integro-differenciál-egyenleteket a 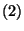 ,
, 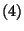 határfeltételek mellett.
határfeltételek mellett.
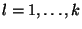
,
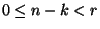
esetén,
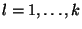
,
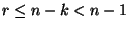
esetén,
valamint
A ![$\left[\ \ \right]^*$](img1637.gif) jelentése a bizonyításban szerepel,
és
jelentése a bizonyításban szerepel,
és
Bizonyítás. Mivel 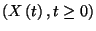 Markov-folyamat, ezért sűrűségfüggvényei
kielégítik a Kolgomorov-Chapman egyenleteket. Tekintsük a folyamatot
rövid
Markov-folyamat, ezért sűrűségfüggvényei
kielégítik a Kolgomorov-Chapman egyenleteket. Tekintsük a folyamatot
rövid 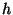 ideig. Ekkor a következő összefüggések igazak:
ideig. Ekkor a következő összefüggések igazak:
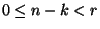
,
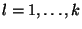
esetén.
Hasonlóan
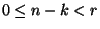
,
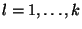
esetén.
Végül
Ezekből az összefüggésekből a tétel állítását
könnyen megkaphatjuk. A felírt összefüggések bal oldalát
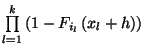 -val osztva, és figyelembe véve
a normált sűrűségfüggvény definícióját, és
-val osztva, és figyelembe véve
a normált sűrűségfüggvény definícióját, és
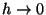 határértéket véve kapjuk a tétel állítását.
A tétel
határértéket véve kapjuk a tétel állítását.
A tétel 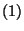 ,
, 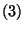 egyenlőségeinek bal oldalán a parciális differenciálhányados
szokásos jelölését használtuk fel. Ezt általában
nem tehetjük meg, mivel a parciális differenciálhányados létezését
nem tettük fel. Ezért használtuk a
egyenlőségeinek bal oldalán a parciális differenciálhányados
szokásos jelölését használtuk fel. Ezt általában
nem tehetjük meg, mivel a parciális differenciálhányados létezését
nem tettük fel. Ezért használtuk a ![$[\ \ ]^*$](img1650.gif) jelölést. Valójában
jelölést. Valójában ![$[\ \ ]^*$](img1650.gif) az
az 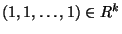 iránymenti deriváltat jelenti. A
iránymenti deriváltat jelenti. A
ergodikus eloszlás meghatározásához meg kell oldani az 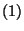 ,
, 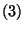 egyenleteket a
egyenleteket a 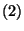 ,
, 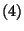 határfeltételek mellett. Legyen
határfeltételek mellett. Legyen
Ekkor behelyettesítéssel ellenőrizhető, hogy kielégítik az
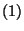 ,
, 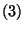 egyenleteket a
egyenleteket a 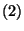 ,
, 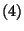 határfeltételek mellett, és ezek a
határfeltételek mellett, és ezek a 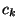 értékek rekurzióval kifejezhetők
értékek rekurzióval kifejezhetők 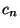 függvényében. Nevezetesen
függvényében. Nevezetesen
Ezek az egyenletek teljesen leírják a rendszer működését.
Jelölje 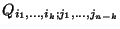 annak a stacionárius valószínűségét,
hogy a termináloknál az
annak a stacionárius valószínűségét,
hogy a termináloknál az 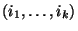 indexű jobok vannak, és a központi egységnél
lévő jobok indexei érkezési sorrendben
indexű jobok vannak, és a központi egységnél
lévő jobok indexei érkezési sorrendben 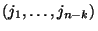 . Továbbá
. Továbbá 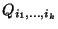 jelölje annak a stacionárius valószínűségét,
hogy az
jelölje annak a stacionárius valószínűségét,
hogy az 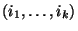 indexű jobok tartózkodnak a termináloknál.
Igazolható, hogy
indexű jobok tartózkodnak a termináloknál.
Igazolható, hogy
A 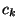 -ra kapott összefüggést felhasználva kapjuk,
hogy
-ra kapott összefüggést felhasználva kapjuk,
hogy
Hasonlóan
Jelölje 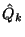 és
és 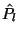 annak a stacionárius valószínűségét,
hogy a termináloknál
annak a stacionárius valószínűségét,
hogy a termináloknál 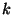 , illetve a központi egységeknél
, illetve a központi egységeknél 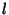 job tartózkodik. Ekkor világos, hogy
job tartózkodik. Ekkor világos, hogy
Könnyen belátható, hogy
ahol 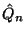 a
a 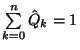 normalizáló feltételéből
határozható meg.
Homogén esetben a következő eredményekhez jutunk.
normalizáló feltételéből
határozható meg.
Homogén esetben a következő eredményekhez jutunk.
Ezért
Ezek az eredmények megegyeznek az 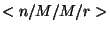 modell stacionárius valószínűségeire
kapott eredményeivel. Látható, hogy ezek az
modell stacionárius valószínűségeire
kapott eredményeivel. Látható, hogy ezek az 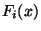 eloszlásfüggvény alakjától nem függnek,
csak az
eloszlásfüggvény alakjától nem függnek,
csak az 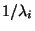 várható értékektől.
várható értékektől.
![]() valószínűségi változó a
valószínűségi változó a ![]() időpontban a terminálnál lévő jobok számát,
időpontban a terminálnál lévő jobok számát,
![]() ezeknek a joboknak az indexeit lexikografikus sorrendben, és
ezeknek a joboknak az indexeit lexikografikus sorrendben, és ![]() a központi egységnél lévő (kiszolgálás alatt lévő
vagy sorbanálló) jobok indexeit érkezésük sorrendjében.
Az
a központi egységnél lévő (kiszolgálás alatt lévő
vagy sorbanálló) jobok indexeit érkezésük sorrendjében.
Az 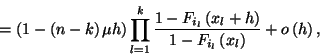
 .
1.Tétel Ha
.
1.Tétel Ha 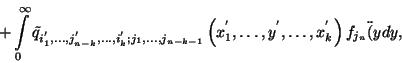
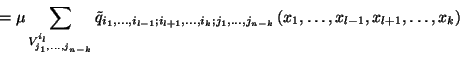
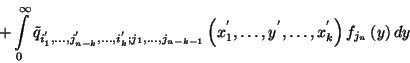
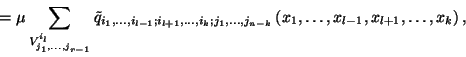
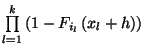 -val osztva, és figyelembe véve
a normált sűrűségfüggvény definícióját, és
-val osztva, és figyelembe véve
a normált sűrűségfüggvény definícióját, és
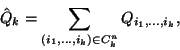
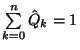 normalizáló feltételéből
határozható meg.
Homogén esetben a következő eredményekhez jutunk.
normalizáló feltételéből
határozható meg.
Homogén esetben a következő eredményekhez jutunk. ![]() modell stacionárius valószínűségeire
kapott eredményeivel. Látható, hogy ezek az
modell stacionárius valószínűségeire
kapott eredményeivel. Látható, hogy ezek az ![]() eloszlásfüggvény alakjától nem függnek,
csak az
eloszlásfüggvény alakjától nem függnek,
csak az ![]() várható értékektől.
várható értékektől.