Problémák
1. Az 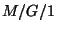 rendszer képleteiből származtassuk az
rendszer képleteiből származtassuk az 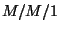 jellemzőit!
jellemzőit!
2. Legyen 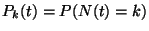 . Továbbá legyen
. Továbbá legyen 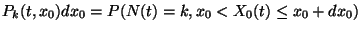 , ahol
, ahol 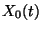 a
a 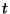 pillanatban a kiszolgálócsatornában tartózkodó
igény eddig már eltelt kiszolgálási ideje. a, Mutassuk meg,
hogy
pillanatban a kiszolgálócsatornában tartózkodó
igény eddig már eltelt kiszolgálási ideje. a, Mutassuk meg,
hogy
ahol
b, Legyen 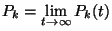 és
és 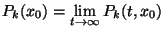 . Az a, pontból a kővetkező stacionárius eredmény
adódik:
. Az a, pontból a kővetkező stacionárius eredmény
adódik:
Igazoljuk az egyensúlyi helyzetre vonatkozó alábbi eredményeket
(ahol 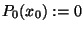 ):
):
c, A b, pontban felírt négy egyenlet meghatározza a stacionárius
valószínűségeket, ha még egy megfelelő normáló egyenletet
is hozzájuk veszűnk. Fejezzük ki ezt a normáló egyenletet
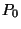 és
és 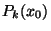 segítségével! d, Legyen
segítségével! d, Legyen 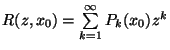 . Mutassuk meg, hogy
. Mutassuk meg, hogy
és
e, Mutassuk meg, hogy a d, pontbeli 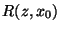 a következő:
a következő:
ahol
f, Legyen 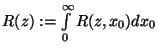 ; mutassuk meg, hogy
; mutassuk meg, hogy
h, 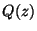 III.1.4-beli definíciójával összhangban definiáljuk
a
III.1.4-beli definíciójával összhangban definiáljuk
a
mennyiséget. Mutassuk meg, hogy az így megadott 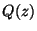 egyenlő az első P-H-transzformáltegyenletben kifejezettel!
egyenlő az első P-H-transzformáltegyenletben kifejezettel!
3. Az 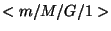 rendszer formuláiból származtassuk az
rendszer formuláiból származtassuk az
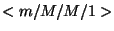 modell megfelelő eredményeit!
modell megfelelő eredményeit!
![]() rendszer képleteiből származtassuk az
rendszer képleteiből származtassuk az ![]() jellemzőit!
jellemzőit!
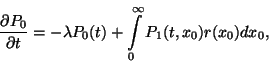
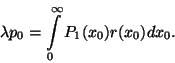
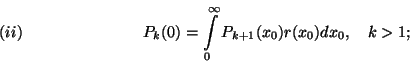
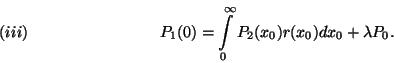
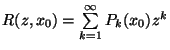 . Mutassuk meg, hogy
. Mutassuk meg, hogy 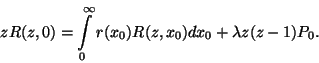
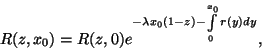
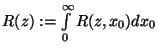 ; mutassuk meg, hogy
; mutassuk meg, hogy ![]() rendszer formuláiból származtassuk az
rendszer formuláiból származtassuk az
![]() modell megfelelő eredményeit!
modell megfelelő eredményeit!