II.6.1. Az  rendszer
rendszer
A gépkiszolgálási probléma esetén ez a diszciplina azt
jelenti, hogy a gépek javítása meghibásodásuk után
rögtön megkezdődik, melynek intenzitása függ a mindenkori
hibás gépek számától, és azzal fordítottan
arányos. Ha egy gép javítás alatt van egy olyan  idő alatt, amikor rajta kívül még
idő alatt, amikor rajta kívül még 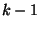 más gép is hibás, akkor ezen
más gép is hibás, akkor ezen  idő alatt egy gép javítási ideje csak
idő alatt egy gép javítási ideje csak  mennyiséggel halad előre. Ekkor a
mennyiséggel halad előre. Ekkor a  folyamat állapotterét az
folyamat állapotterét az 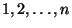 számok
számok 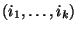
 kombinációi alkotják, és ezekhez még
hozzá kell venni a
kombinációi alkotják, és ezekhez még
hozzá kell venni a 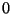 pontot (minden gép működik). Legyenek
pontot (minden gép működik). Legyenek 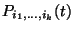
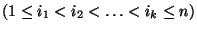 a
a  lánc
lánc 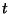 pillanatbeli eloszlását leíró függvények.
Ekkor a Kolgomorov-egyenletek a következők:
pillanatbeli eloszlását leíró függvények.
Ekkor a Kolgomorov-egyenletek a következők:
ahol 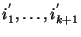 az
az 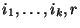 egészeknek a nagyság szerinti rendezése,
és
egészeknek a nagyság szerinti rendezése,
és
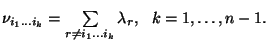
ahol a megfelelő indexek értelemszerű értékeket vesznek fel. A
stacionárius eloszlás, amely azonos a
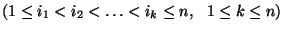 , ergodikus eloszlással,
a
, ergodikus eloszlással,
a
homogén lineáris egyenletrendszernek a 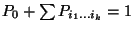 feltételt kielégítő egyértelmű
megoldása, ahol az összegzés n elem összes kombinációira
terjed ki. Egyszerű helyettesítéssel belátható, hogy ennek
az egyenletrendszernek a megoldása a
feltételt kielégítő egyértelmű
megoldása, ahol az összegzés n elem összes kombinációira
terjed ki. Egyszerű helyettesítéssel belátható, hogy ennek
az egyenletrendszernek a megoldása a 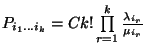 , ahol
, ahol 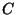 a normalizáló feltételből határozható meg.
a normalizáló feltételből határozható meg.
![\begin{displaymath}P_0^{'}\left(t\right)=-\left[\sum_{i=1}^n \lambda_i\right]
P_0\left(t\right)+\sum_{i=1}^n\mu_i P_i\left(t\right),\end{displaymath}](img901.gif)
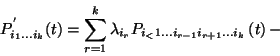
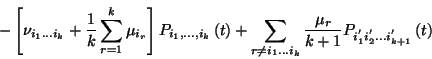
![\begin{displaymath}P_{1,\ldots,n}^{'}(t)=\sum_{r=1}^n \lambda_r P_{1,\ldots,r-1,r+1,]\ldots,n}
(t) -\end{displaymath}](img907.gif)
![\begin{displaymath}-\left[{1\over n}\sum_{r=1}^n\mu_r\right] P_{1,\ldots,n}(t),\end{displaymath}](img908.gif)
![\begin{displaymath}\left[\sum_{i=1}^n\lambda_i\right]P_0= \sum_{i=1}^n \mu_iP_i,\end{displaymath}](img912.gif)
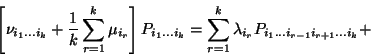
![\begin{displaymath}\left[{1\over n}\sum_{r=1}^n\mu_r\right] P_{1,\ldots,n}=\sum_{r=1}^n \lambda_r
P_{1\ldots,r-1,r+1,\ldots,n}\end{displaymath}](img915.gif)
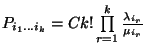 , ahol
, ahol