II.6.2. Az $<n/\vec{M}/\vec{M}/1/FIFO>$rendszer


A gépek javításai történjenek a meghibásodás sorrendjében. Ekkor a $\xi(t)$folyamat állapotterét $n$elem összes $1\le k\le n$rendû ismétlés nélküli variációi alkotják, amelyekhez még a $0$pontot is csatolni kell ( a $0$pont annak az esetnek a megfelelõje, amikor mindegyik gép mûködik ). A $\xi(t)$lánc $t$$(t\ge 0)$pillanatbeli eloszlására vezessük be az alábbi függvényeket. Ha $v(t)$jelöli a $t$idõpontban nem mûködõ gépek számát, $x_i(t)$a nem mûködõ gépek indexét $\left(i=1,\ldots,v\left(t\right)\right)$meghibásodásuk sorrendjében, akkor a lánc $t$pillanatbeli eloszlását leíró függvények:

\begin{displaymath}P_0\left(t\right)=P\left(v\left(t\right)=0\right),\end{displaymath}


 

\begin{displaymath}P_{i_1\ldots i_k}\left(t\right)=P\left(v\left(t\right)=k,\ x_1\left(t\right)=i_1,\ldots,x_k\left(t\right)=i_k\right),\end{displaymath}


ahol $(1\le k\le n)$, $(1\le i_1,\ldots,i_k\le n)$. Ezek a függvények kielégítik a következõ differenciálegyenlet-rendszert


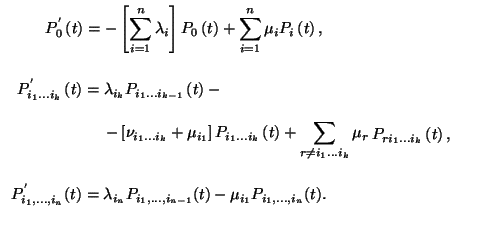
\begin{displaymath} \eqalign{ P_0^{'}\left(t\right)=&-\left[\sum_{i=1}^n \lam... ...i_1,\ldots,i_{n-1}}(t)- \mu_{i_1} P_{i_1,\ldots,i_n}(t).\cr} \end{displaymath}


A stacionárius eloszlás, mely azonos a

\begin{displaymath}P_0=\lim_{t\to\infty} P_0\left(t\right) ,\end{displaymath}


 

\begin{displaymath}P_{i_1\ldots i_k}=\lim_{t\to\infty}P_{i_1\ldots i_k}\left(t\right)\end{displaymath}


$(1\le i_1,i_2,\ldots,i_k\le n,\ \ 1\le k\le n)$ergodikus eloszlással, a

\begin{displaymath} \eqalign{ \left[\sum_{i=1}^n\lambda_i\right]P_0=&\sum_{i=1... ... \sum_{r\ne{i_1\ldots i_k}} \mu_rP_{ri_1 i_2\ldots i_k},\cr} \end{displaymath}


 

\begin{displaymath}\mu_{i_1} P_{i_1,\ldots,i_n}=\lambda_{i_n} P_{i_1,\ldots,i_{n-1}}\end{displaymath}


homogén lineáris egyenletrendszerneik a $P_0+\sum P_{i_1\ldots i_k}=1$feltételt kielégítõ egyértelmû megoldása, ahol az összegzés n elem összes variációjára terjed ki. Az egyenletrendszer könnyebben kezelhetõvé válik, ha bevezetjük a következõ vektorváltozókat. Legyen $Z^{\left(k\right)}$$(1\le k\le n)$ $V^n_k={n\choose k}k!$dimenziós vektor, amelynek a komponensei az $1,2,...n$számok $k$-ad osztályú, lexikografikusan rendezett $i_1,\ldots,i_k$variációihoz tartozó $P_{i_1\ldots i_k}$valószínûségek. Ekkor az egyenletrendszer az alábbi differenciaegyenlet-rendszerbe megy át:


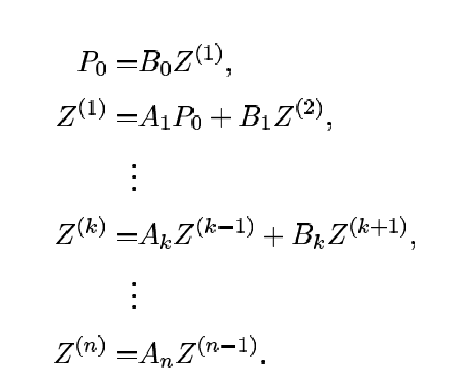
Itt most $1\le k\le n$-re $A_k$ $V_k^n\times V_{k-1}^n$-es mátrix, $0\le k<n$-re $B_k$ $V_k^n \times V_{k+1}^n$-es mátrix, és elemeik az egyenletrendszerbõl könnyen meghatározhatók. Legyen $F_n=A_n$és tetszõleges $1\le k<n$esetén $F_k={\left(I-B_kF_{k+1}\right)}^{-1}A_k$. Ekkor $Z^{\left(k\right)}=F_kZ^{\left(k-1\right)}$$(1\le k\le n)$, ahol $Z^{\left(0\right)}=P_0$. Egy tetszõleges $P_0$értékbõl a $Z^{\left(k\right)}$$(1\le k\le n)$vektorok rendre meghatározhatók. A $P_{i_1\ldots i_k}$valószínûségeket a normalizáló feltétel figyelembe vétele után e vektorok komponensei szolgáltatják.

 

Nyitólap    Tartalomjegyzék    Fejezetek ( B I II III IV F )    Letöltések
FRAME-mel FRAME nélkül
<<   Előző Következő  >>