Abszolút prioritásos kiszolgálási elv esetén a
Abszolút prioritásos kiszolgálási elv esetén a ![]() folyamat állapotterét az
folyamat állapotterét az ![]() számok
számok ![]()
![]() kombinációi alkotják, és ezekhez még
hozzá kell venni a
kombinációi alkotják, és ezekhez még
hozzá kell venni a ![]() pontot (minden gép működik ). Legyenek
pontot (minden gép működik ). Legyenek ![]()
![]() a
a ![]() lánc
lánc ![]() pillanatbeli eloszlását leíró függvények.
Ekkor a Kolgomorov-egyenletek a következők:
pillanatbeli eloszlását leíró függvények.
Ekkor a Kolgomorov-egyenletek a következők:
![\begin{displaymath}P_0^{'}\left(t\right)=-\left[\sum_{i=1}^n \lambda_i\right]
P_0\left(t\right)+\sum_{i=1}^n\mu_i P_i\left(t\right),\end{displaymath}](img901.gif)
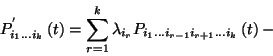
![\begin{displaymath}-\left[\nu_{i_1\ldots i_k}+\mu_{i_1}\right]P_{i_1\ldots i_k}\left(t\right)
+\sum_{r=1}^{i_1-1} \mu_r P_{ri_1\ldots i_k}(t) ,\end{displaymath}](img949.gif)
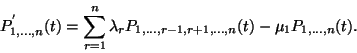
![\begin{displaymath}\left[\sum_{i=1}^n\lambda_i\right]P_0= \sum_{i=1}^n \mu_iP_i,\end{displaymath}](img912.gif)
![\begin{displaymath}\left[\nu_{i_1\ldots i_k}+\mu_{i_1}\right] P_{i_1\ldots i_k}=...
..._{r=1}^k
\lambda_{i_r} P_{i_1\ldots i_{r-1}i_{r+1}\ldots i_k}+\end{displaymath}](img953.gif)
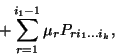
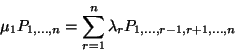
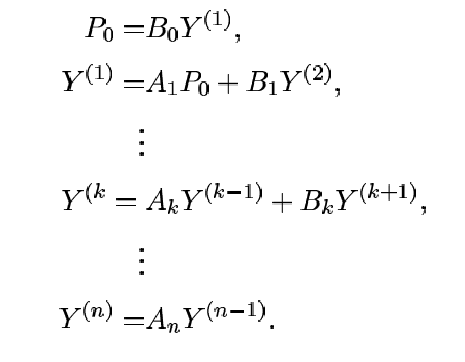
Itt most ![]() -re
-re ![]()
![]() -es mátrix,
-es mátrix, ![]() -re
-re ![]()
![]() -es mátrix, és elemeik egyenletrendszerből
kiolvashatók. Ezt a differencia egyenletrendszert ugyanúgy oldhatjuk
meg, mint a FIFO kiszolgálás esetén.
-es mátrix, és elemeik egyenletrendszerből
kiolvashatók. Ezt a differencia egyenletrendszert ugyanúgy oldhatjuk
meg, mint a FIFO kiszolgálás esetén.
|